Логарифмические частотные характеристики типовых звеньев.

Построение АФХ, АЧХ и ФЧХ в реальном масштабе частот затруднительно из-за большого диапазона изменения частот. Теоретически, частота должна меняться от 0 до ∞. Поэтому для упрощения построения и проведения расчетов используют построение логарифмических АЧХ и ФЧХ, построенных прежде всего в логарифмическом масштабе частот. Как правило, частоты разбиваются по декадам ,т. е. с коэффициентом 10, например: 0,001; 0,01; 0,1; 1; 10; 100; 1000, если на оси откладывается сама частота ω или -3; -2 ; -1; 0; 1; 2; 3, если на оси откладывается lg ω (рис. 19).

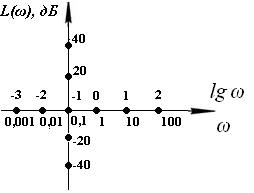
Рис. 19. Разбиение шкал ωи lg ω на декады, шкалы L(ω) на децибелы

Из примера видно, что можно продолжать ось частот влево к 0 и вправо к ∞. Следовательно, ось ординат L(ω) может также перемещаться и служит только для определения масштаба.

Для логарифмической фазовой частотной характеристики (ЛФЧХ) значение ординаты меняется в незначительном диапазоне и проставляется в естественном масштабе, т. е. в радианах или градусах. Для амплитудной характеристики, у которой, как известно, АЧХ, например, интегратора, начинается из ∞, используется также логарифмический масштаб. В результате, логарифмическая амплитудная частотная характеристика (ЛАЧХ) представляется в виде 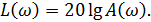Измеряется эта характеристика в децибелах (дБ). Например, если на частоте ω₁ A(ω₁) = 100, то L(ω₁)=20 lg 100 =40 дБ (см. рис. 19).

Любая передаточная функция типового звена, за исключением элементарных, представляет собой произведение элементарных типовых звеньев, т. е. 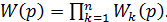Полагая p = jω, получим выражение АФХ системы:

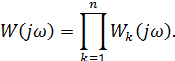
ЛАЧХ равна:

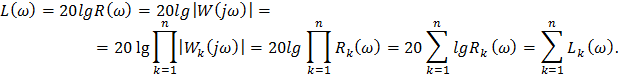
Следовательно, ЛАЧХ сложного звена представляет собой алгебраическую сумму ЛАЧХ отдельных сомножителей, причем из числителя в сумму характеристика входит со знаком плюс, а из знаменателя передаточной функции – со знаком минус.

Аналогично и ЛФЧХ представляет собой алгебраическую сумму отдельных фазовых характеристик 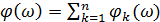и в эту сумму фазовые характеристики из числителя входят со знаком плюс, т. е. дают положительный фазовый сдвиг, а из знаменателя с минусом, т. е. дают отрицательный фазовый сдвиг.

Таким образом, для построения ЛЧХ необходимо иметь характеристики отдельных сомножителей, а затем сложить их с соответствующими знаками.