Передаточные функции. Преобразование Лапласа и его свойства.

Одной из основных форм математической модели динамических звеньев является передаточная функция устройства, которая получается путём интегрального преобразования Лапласа дифференциального уравнения. Суще-ствует прямое преобразование Лапласа:

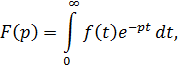
где f(t) – оригинал, F(p) – изображение.

Также существует обратное преобразование Лапласа:

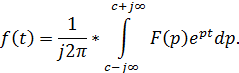
Эти уравнения часто записывают в сокращенном виде:

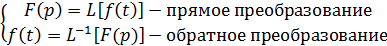
Передаточная функция устройства определена как изображение выходной величины y(p) к изображению входной величины x(p) при нулевых начальных условиях. Обозначается:

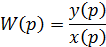
В таблице 1 приведены основные свойства и теоремы преобразования Лапласа, которые используются при переходе к операторной форме дифферен-циального уравнения и определении передаточной функции.

Таблица 1. Преобразования Лапласа

Наименование	Оригинал	Изображение Лапласа
Свойство линейности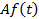
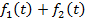
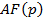
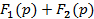
Теорема подобия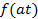
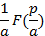
Теорема запаздывания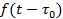
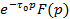
Теорема смещения в комплексной плоскости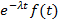
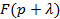
Правило дифференцирования при нулевых начальных значениях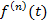
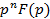
Правило интегрирования при нулевых начальных значениях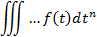
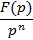
Теорема о конечном значении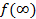
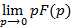
Теорема о начальном значении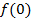
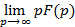
Единичная импульсная функция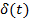
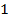
Единичная ступенчатая функция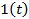
Неединичная ст. ф-ция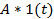

Таблица 1. (Окончание)

Наименование	Оригинал	Изображение Лапласа
Степенная функция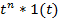
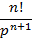
Экспонента
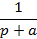
Смещенная экспонента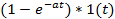
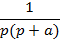
Синусоида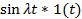
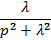
Косинусоида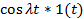
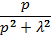
Затухающая синусоида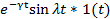
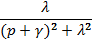
Затухающая косинусоида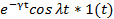

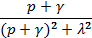
В частности, в этом случае используется свойство линейности и правило дифференцирования при нулевых начальных условиях.

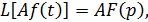
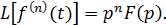
Рассмотрим примеры получения передаточных функций типовых звеньев.