Частотные характеристики.

Эти характеристики также являются одной из моделей динамических свойств технических устройств. Типовым входным сигналом является синусоидальное воздействие x(t) = asin ωt с фиксированной амплитудой и изменяю-щейся частотой от 0 до ∞. Если на вход устройства подать такой сигнал с фиксированной частотой ω₀, то на выходе устройства после окончания переходного процесса также получим синусоиду такой же частоты ω₀, но с измененной на коэффициент A амплитудой и сдвинутой по фазе относительно входного сигнала на угол φ, т. е. 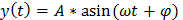. При увеличении частоты будут меняться и коэффициент A и значение угла φ. Зависимость A = A(ω) называется амплитудно-частотной характеристикой устройства (АЧХ). Она показывает, как изменяется амплитуда выходного сигнала, проходя через устройство на разных частотах. Величина φ = φ(ω) называется фазо-частотной характеристикой устройства (ФЧХ) и показывает, какой сдвиг по фазе может быть получен между входным и выходным сигналами на разных частотах. И АЧХ, и ФЧХ для многих устройств может быть получено экспериментально. У типовых звеньев инерционного типа с увеличением частоты АЧХ стремится к нулю, у звеньев дифференцирующего типа – наоборот.

Аналитическое выражение для АЧХ и ФЧХ получают с использованием амплитудно-фазовой характеристики АФХ, которая рассматривается как модуль и аргумент комплексного числа 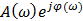, изображаемого для определения частоты ω точкой на комплексной плоско-сти. В этом случае входной сигнал также заменяется комплексным числом вида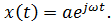

При изменении частоты от 0 до ∞, точка перемещается по комплексной плоскости, описывая кривую, которая называется амплитудно-фазовой характеристикой, либо гадографом (рис.18).

Как видно из рисунка 18, вектор, проведенный из начала координат в точку с частотой ω₀, может перемещаться на плоскости и угол его поворота относительно положительной действительной оси представляет собой фазовый сдвиг, или ФЧХ, причем поворот против часовой стрелки дает положительный фазовый сдвиг, а по часовой – отрицательный. Поскольку АФХ представляет собой комплексное выражение, то она может быть представлена в виде суммы вещественной U(ω) и мнимой V(ω) частей:

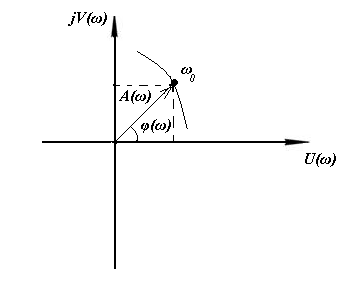
Рис. 18. Гадограф

Из рис.18 также очевидно, что вектор 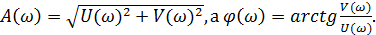Математическое выражение для АФХ получается заменой оператора p на jω в выражении передаточной функции типового звена:

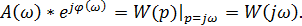
АФХ звена часто называют частотной передаточной функцией. Зная выражение для АФХ, всегда можно найти аналитическое выражение для АЧХ и ФЧХ любого типового звена. Учитывая то, что типовые звенья – дробно-рациональные функции и представляют собой произведения элементарных звеньев, целесообразно находить АЧХ от каждого элементарного звена в числителе и знаменателе. По аналогии, ФЧХ находится как алгебраическая сумма фазовых характеристик элементарных звеньев, причем от числителя частотной передаточной функции arctg имеет знак «+», а от знаменателя знак «-». В качестве примеров получим АЧХ и ФЧХ нескольких типовых звеньев.

1) Безынерционное звено

АФХ: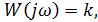

АЧХ:

ФЧХ:

Этот результат следовало ожидать, т. к. рассматриваем звено без динамических свойств. Фазовый сдвиг равен 0, а модуль остается неизменным во всем диапазоне частот.

2) Инерционное звено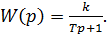

АФХ: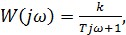

АЧХ: ,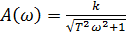

ФЧХ:

Как видно из выражения для АЧХ, с увеличением частоты, A(ω) умень-шается от величины k до 0 и звено вносит отрицательный фазовый сдвиг, который увеличивается с увеличением частоты.

ω		∞
φ(ω)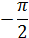

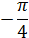
3) Изодромное звено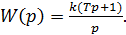

АФХ:

АЧХ: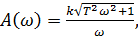

ФЧХ: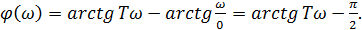

Анализ фазовой характеристики показывает, что идеальный интегратор имеет постоянную отрицательную фазовую характеристику, равную π/2, а форсирующее звено – положительный фазовый сдвиг от 0 до +90, поэтому при увеличении частоты, отрицательный фазовый сдвиг уменьшается от –π/2 до 0.

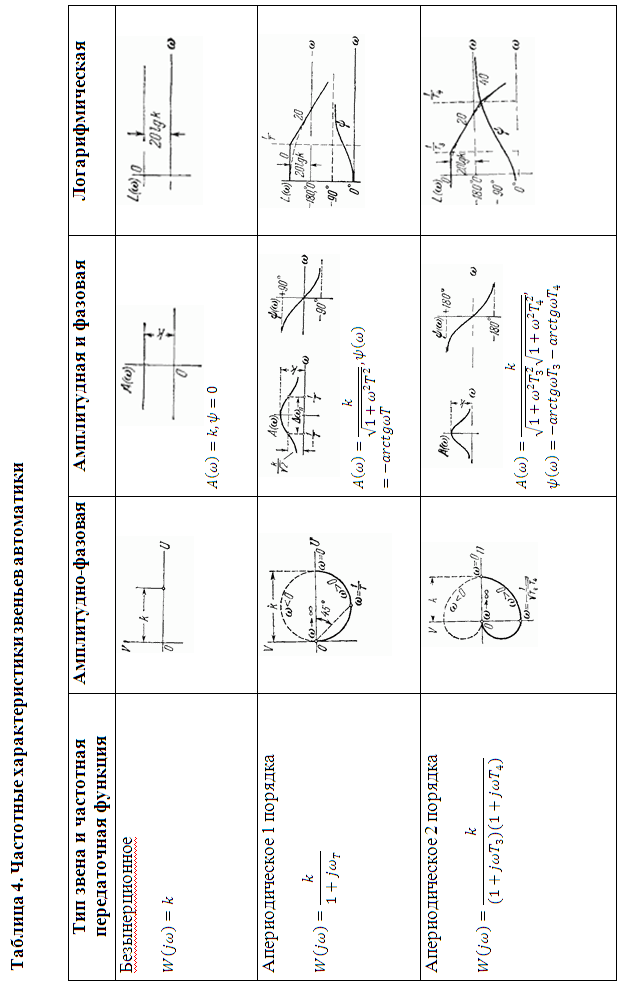
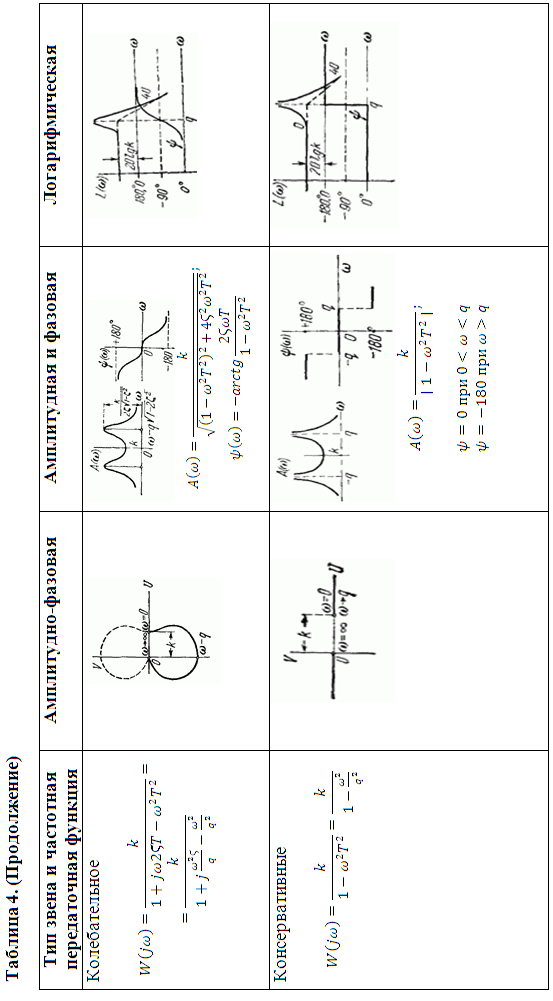
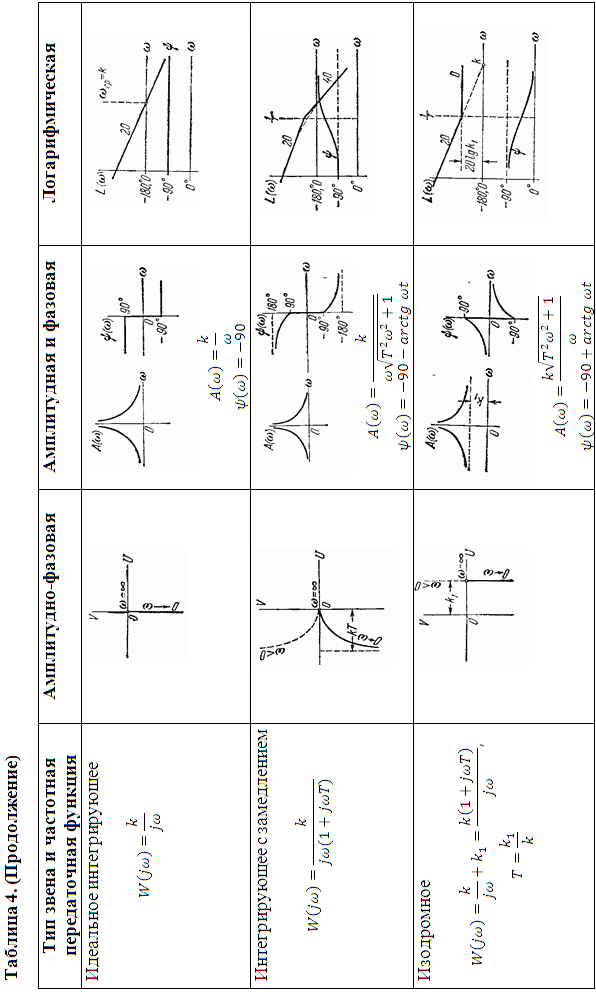
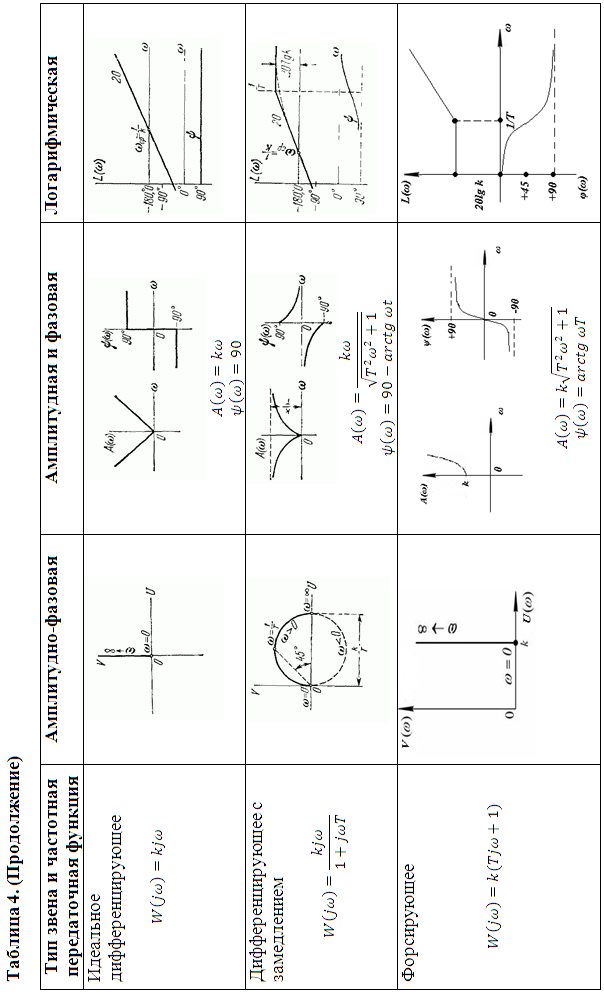
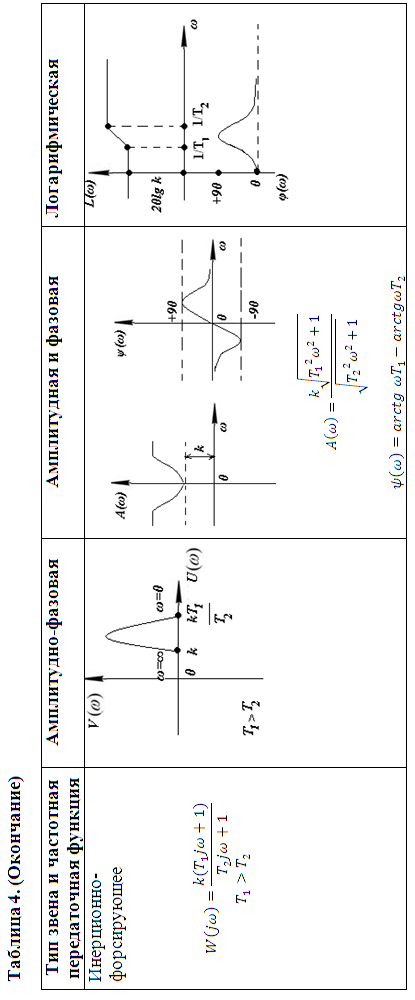
АФХ, АЧХ, ФЧХ типовых звеньев приведены в таблице 4 в виде примерных графиков и по полученным выражениям всегда могут быть построены и для конкретных значений.