Эквивалентные передаточные функции типовых соединений.

Мы отметили, что наличие различных динамических свойств (инерцио-нных и форсирующих) определяется наличием производных по выходным и входным величинам в дифференциальных уравнениях.

Следовательно, основными простыми звеньями являются идеальный интегратор, идеальный дифференциатор и безынерционное звено (масштаби-рующий коэффициент). Все остальные, более сложные звенья, могут быть получены с помощью различных соединений простых звеньев. Простые звенья можно соединить последовательно, параллельно или выполнить соединения в виде местной обратной связи.

При последовательном соединении (рис. 13, а) выходная величина каждого из звеньев, кроме последнего, служит входной величиной последующе-го звена. Эквивалентная передаточная функция последовательного соединения n звеньев равна произведению передаточных функций этих звеньев:

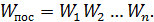
При параллельном соединении (рис. 13, б) все звенья имеют одну и ту же входную величину, а их выходные величины суммируются. Передаточная функция параллельного соединения n звеньев равна сумме передаточных функций этих звеньев:

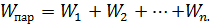
Третье типовое соединение (рис. 13, в), называемое встречнопараллельным (местная обратная связь) состоит из двух звеньев. Звено с передаточной функцией W_П является прямой цепью передачи сигналов, а звено с передаточной функцией Wo осуществляет обратную связь. Обратная связь — это воздействие выходной величины какого-то звена на его вход. Если это воздействие совпадает по знаку с входной величиной, то обратная связь положительная. В противном случае обратная связь отрицательная.

Эквивалентная передаточная функция встречно-параллельного соеди-нения:

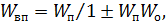
где знак + в знаменателе соответствует отрицательной обратной связи (ООС) и знак - положительной (ПОС).

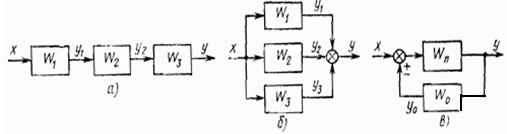
Рис. 13. Типовые соединения динамических звеньев

Используя основные соединения типовых элементарных звеньев: интегрирующего, дифференцирующего и безынерционного, можно получить любое сложное типовое звено.

1. Рассмотрим применения последовательного соединения:

а) Пусть необходимо получить передаточную функцию типового звена 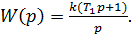Это звено состоит из 3 типовых, последовательно соединенных: безынерционного (k), форсирующего (Tp+1) и интегрирующего (1/p).

б) Аналогичным образом, инерционное звено 2 порядка 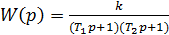– 2 последовательно включенных инерционных звена 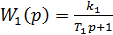и

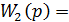
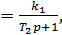где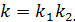

2. Рассмотрим применения параллельного соединения:

а) Пусть .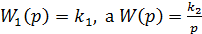

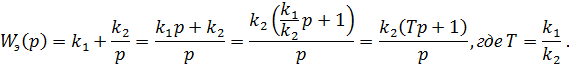
Следовательно, получено изодромное звено.

б) Пусть 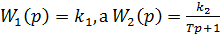. Тогда:

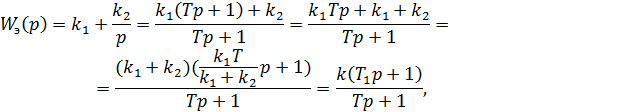
где 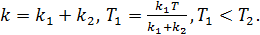Получили инерционно-форсирующее звено с преобладанием инерционного эффекта.

Из примеров следует, что параллельное соединение сохраняет динамические свойства подключаемого звена с добавлением инерционных.

Соединения с другими звеньями приведены в табл.2.

Таблица 2. Параллельные соединения типовых динамических звеньев

Таблица 2. (Окончание)

3. Рассмотрим свойства соединений с встречно-параллельной (местной обратной) связью. На примерах отметим свойства 2 характерных случаев:

а) в прямой цепи – безынерционное звено, а в обратной – динамическое;

б) в прямой цепи – динамическое звено, а в обратной – безынерционное.

Для 1 случая:

1) Пусть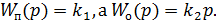

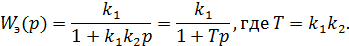
Получили инерционное звено.

2) Пусть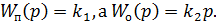

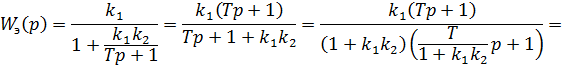
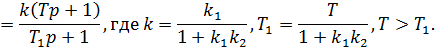
Получили инерционно-форсирующее звено с преобладанием форсирующего эффекта.

Как видно из примеров, в эквивалентной передаточной функции инвертируются динамические свойства звена обратной связи.

Для 2 случая:

1) Пусть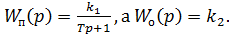

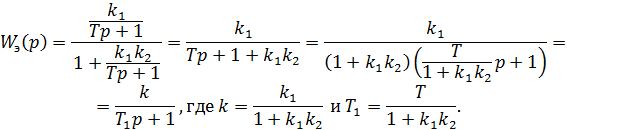
Получили инерционное звено 1 порядка. То есть, эквивалентное соединение сохраняет динамические свойства прошлой цепи.

2) Пусть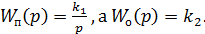

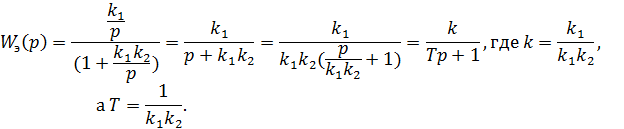
Получили инерционное звено 1 порядка.

Заметим, что с помощью этого соединения можно получить инерционное звено и общее свойство такого соединения сохраняется.