Вариационные ряды и их характеристики. Доверительные интервалы.

1. Дан точечный вариационный ряд. Определить выборочные характеристики, построить полигон частот, ЭФР.

а)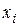

б)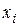

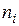
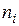
2. Дан интервальный вариационный ряд. Определить выборочные характеристики, построить гистограмму частот, ЭФР.

а)

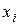
	10-15	15-20	20-25	25-30	30-35

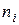
б)

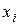
	2-5	5-8	8-11	11-14

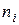
в)

	1-5	5-9	9-13	13-17	17-21

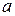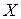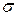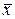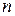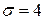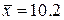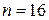3.([5],502) Найти доверительный интервал для оценки с надежностью 0.99 неизвестного математического ожидания нормально распеределенного признака генеральной совокупности, если известны генеральное среднее квадратическое отклонение , выборочная средняя и объем выборки : а) , , ; б) , , .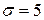

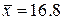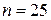4. .([5],507 ) Найти минимальный объем выборки, при котором с надежностью 0.925 точность оценки математического ожидания по выборочной средней равна 0.2, если известно среднее квадратическое отклонение генеральной совокупности .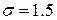

5. .([5],511) По данным 16 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений 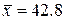и несмещенное среднее квадратическое отклонение 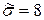. Оценить истинное значение измеряемой величины с надежностью 0.999.

6. .([5],513) По данным объема 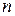из генеральной совокупности нормально распределенного признака найдено несмещенное («исправленное») среднее квадратическое отклонение 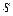. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение 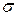с надежностью 0.999, если: а) 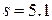, 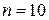; б) , .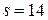

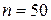7. Среднее значение дальности до ориентира, полученное по четырем независимым измерениям, 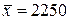м. Средняя квадратическая ошибка прибора 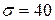м. Найти с надежностью 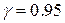доверительный интервал для оценки истинного значения измеряемой величины.

8. В качестве оценки расстояния до навигационного знака принимают среднее арифметическое результатов независимых измерений расстояния 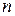дальномерами. Измерения не содержат систематической ошибки, а случайные ошибки распределены нормально со средним квадратическим отклонением 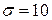м. Сколько надо иметь дальномеров, чтобы абсолютная величина ошибки при определении дальности до навигационного знака с вероятностью 0.9 не превышала 15 м.?