Динамические и статические свойства технических устройств и переход к типовым дифференциальным уравнениям.

Для того, чтобы изучить свойства сложной физической системы(технического устройства) и научиться управлять ей, необходимо получить ее математическую модель. Для этого требуется установить все взаимосвязи между переменными, характеризующими поведение устройства. Поскольку все реальные объекты по своей природе являются динамическими, то для их описания естественно использовать дифференциальные уравнения. Если, кроме того, эти уравнения могут быть линеаризованы, то тогда можно воспользоваться преобразованием Лапласа. В действительности, сложность устройства и игнорирование ряда привходящих факторов обуславливают возникновение некоторых допущений, связанных с функционированием данного устройства. Поэтому часто бывает полезно игнорировать эти допущения и произвести линеаризацию объекта. В результате, на основании физических законов, описывающих поведение эквивалентной линейной системы, можно получить систему дифференциальных уравнений. Наконец, используя математический аппарат, такой, как преобразование Лапласа, мы сможем получить решение, характеризующее поведение данного устройства. В итоге алгоритм исследование динамики объекта сводится к следующему:

1. Определить техническое устройство и его компоненты.

2. Составить математическую модель и выдвинуть необходимые допущения.

3. Записать дифференциальные уравнения, описывающие поведение модели.

4. Решить уравнения относительно желаемых выходных переменных.

5. Проанализировать решения и допущения.

6. При необходимости провести повторный анализ или синтез модели.

Дифференциальные уравнения, описывающие динамику физического объекта, получаются на основании фундаментальных физических законов. Этот метод в равной степени применим к механическим, электрическим, гидравлическим и термодинамическим системам. Рассмотрим апериодическое звено первого порядка(или, другими словами, инерционное звено). Звено описывается дифференциальным уравнением:

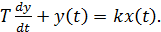(1)

В качестве первого примера (рис. 1) рассмотрим двигатель любого типа (электрический, гидравлический, пневматический и т.д.), механические характеристики которого (зависимость вращающего момента от скорости) могут быть представлены в виде параллельных прямых (рис.2).

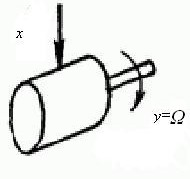
Рис. 1. Схематичное изображение двигателя

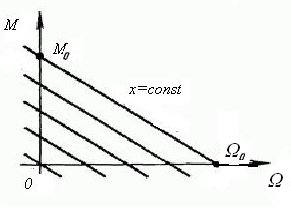
Рис. 2. Механические характеристики двигателя

Входной величиной x здесь является управляющее воздействие в двигателе, например подводимое напряжение в электрическом двигателе, расход жидкости в гидравлическом двигателе и т. п. Выходной величиной является частота вращения Ω. Дифференциальное уравнение движения при равенстве нулю нагрузки может быть представлено в виде:

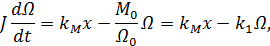
где J - приведенный к валу двигателя суммарный момент инерции; k_M – коэффициент пропорциональности между управляющим воздействием x и вращающим моментом; k₁ = M₀/Ω₀ – наклон механической характеристики, равный отношению пускового момента к скорости холостого хода при некотором значении управляющего воздействия.

Это уравнение приводится к виду:

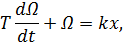
где k = k_M/k₁ – коэффициент передачи звена, 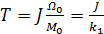– постоянная времени двигателя. Оно полностью совпадает с (1).

В качестве второго примера (рис.3) приведем электрическую L-R цепь, которая также представляет из себя инерционное звено (апериодическое звено первого порядка).

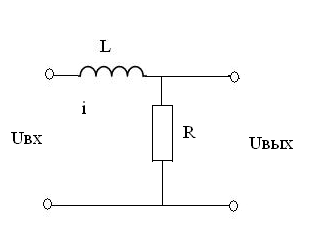
Рис. 3. Пассивная L-R цепь

Аналогично с первым примером, покажем приведение дифференциально-го уравнения для LR-цепи, имея в виду входное и выходное воздействие U_вх = x, U_вых = y

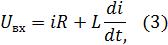
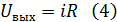
Из уравнения (4) можем выразить ток i:

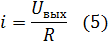
Подставив (5) в (3), получим:

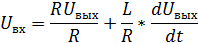
Зная, что 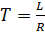и сократив R/R, получим

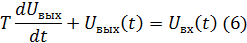
Видим, что с учетом коэффициента k и помня, что U_вх = x, U_вых = y, уравнение (6) так же полностью совпадает с уравнением (1), что доказывает, что вне зависимости от физической природы устройства, мы приходим к одному и тому же дифференциальному уравнению, где T – постоянная времени, измеряемая в секундах, а k – статический коэффициент передачи, который может быть как безразмерным (как во втором примере) и размерным (первый пример). Следовательно, можно говорить о типовых звеньях и типовых уравнениях, которые описывают поведение целого ряда устройств. Принято при записи типовых уравнений слева записывать выходную величину (y(t)) со всеми ее преобразованиями, а справа, относительно знака равенства, входную величину x(t) также со всеми ее преобразованиями. В зависимости от этого, можно выделить алгебраические уравнения, дифференциальные уравнения первого порядка и дифференциальные уравнения второго порядка. Такой набор уравнений с достаточной степенью точности описывает основные технические устройства. Далее рассмотрим уравнения типовых звеньев и отметим, какие технические устройства имеют такие модели.