Построение четвертой гармонической точки с использованием свойств полного 4-вершинника

Задача. На прямой даны три точки - A, B, C. Построить четвёртую гармоническую точку D.

Решение. Мы должны подобрать какой-либо четырёхвершинник для которого точки А, В будут вершинами, а точка С одной из диагональных точек. При этом четвертая гармоническая точка будет пересечением диагонали со стороной (АВ).

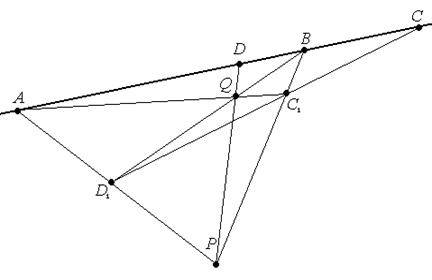
Построение:

1. Берем произвольную точку Р 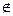(АВ).

2. Проводим прямые (АР) и (ВР).

3. Через точку C проводим произвольную прямую с, так что Р 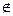с.

4. С₁= (ВР) ∩ с, D₁ = (АР) ∩ с, Q = (АС₁)∩(ВD₁ ).

5. В четырехвершиннике АВС₁D₁ точки Р , Q , С – диагональные. Тогда (РQ)∩(АВ)= D - искомая.

Замечание: Если C – середина AB, тогда D будет бесконечно удаленной точкой.

Рассмотрим частные случаи полного четырёхвершинника на расширенной евклидовой плоскости.

· Одна из диагональных точек - несобственная.

Например, точка R_∞ (АD) || (ВС) АВСD – трапеция.

(AD,LR_∞)= (BC,NR_∞) = - 1

по свойству гармонических четвёрок

точка L -середина отрезка AD,

а точка N - середина отрезка BC.

Вывод:Прямая проходящая через точку пересечения продолжений боковых сторон и точку пересечения диагоналей трапеции делит основания трапеции пополам. (Теорема о четырёх точках трапеции).

· Две диагональные точки несобственные.

Например, точки Р_∞ и R_∞ (АD) || (ВС) и (АВ) || (СD) АВСD – параллелограмм.

Так как прямая (Р_∞R_∞)- несобственная, то точки F, G тоже несобственные (АC,QG_∞)=(BD,QF_∞)=-1

точка Q - середина отрезков АС и BD.

Вывод: Точка пересечения диагоналей параллелограмма делит диагонали пополам.

(Свойство параллелограмма).