Гармонические свойства полного четырехвершинника
Теорема. На каждой стороне полного четырехвершинника есть четвёрка гармонических точек, состоящая из двух вершин и двух точек пересечения этой стороны с диагональным трехвершинником.
Теорема. На каждой диагонали полного четырехвершинника есть четвёрка гармонических точек, состоящая из двух диагональных точек и двух точек пересечения этой диагонали со сторонами четырехвершинника.
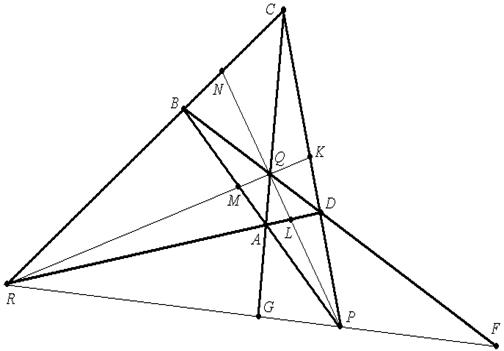
Гармоническими четверками будут на сторонах:
(AB,PM)=(АC,QG)=(AD,RL)=(BC,RN)=(BD,QF)=(CD,PK)= -1.
на диагоналях: (PQ,NL)=(PR,FG)=(RQ,MK)= -1.
Доказательство. Рассмотрим репер R( A, B, C, D ). Тогда A 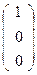 , B
, B 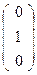 , C
, C 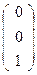 , D
, D 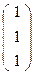 .
.
Точка Р является проекцией единичной точки D из третьей базисной точки С на координатную прямую (АВ)  Р
Р 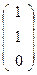 .
.
Точка Q является проекцией единичной точки D из второй базисной точки В на координатную прямую (АС)  Q
Q 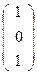 .
.
Точка R является проекцией единичной точки D из первой базисной точки А на координатную прямую (ВС)  R
R 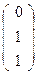 .
.
М 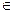 (АВ)
(АВ)  х3 = 0.
х3 = 0.
М 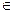 (QR)
(QR) 
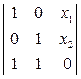 =0
=0  - х1 – х2 = 0
- х1 – х2 = 0  - х1 = х2
- х1 = х2  М
М 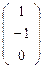 .
.
Точки A 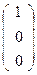 , B
, B 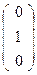 , Р
, Р 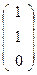 , М
, М  лежат на одной прямой и подсчет сложного отношения дает (АВ,РМ)= - 1.
лежат на одной прямой и подсчет сложного отношения дает (АВ,РМ)= - 1.
Гармонизм других четверок можно доказать аналогично. □
Другой способ доказательства для других четверок основан на свойстве (7) сложного отношения (самостоятельно).
Замечание: В силу принципа двойственности верна теорема для четырехсторонника. (сам-но).
Дата добавления: 2022-02-05; просмотров: 558;











