Задачи на построение.

Задача 1. Даны прямые а || b, точки А, В 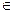а. С помощью линейки построить середину отрезка АВ.

Решение. Так прямые параллельны будем использовать частный случай четырехвершинника – трапецию.

Построение:

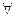1. Берем Р неинцидентную прямым а и b.

2. Проводим прямые (АР) и (ВР).

3. Строим точки

С=(АР)∩b,

D=(ВР)∩b.

4. Q = (СВ)∩(АD).

5. (РQ)∩(АВ)= М - искомая середина отрезка.

Задача 2. Даны точки А, В, С 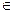а и точка D 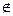а , причем точка С - середина отрезка АВ. С помощью линейки, через точку D провести прямую b ||а.

Решение. Так как необходимо построить параллельную прямую, будем использовать частный случай четырехвершинника – трапецию.

Построение:

1. Проводим (АD).

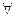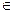2. Берем Р (АD),

Р≠А, Р≠D.

3. Проводим прямые (СР), (ВР) и (ВD).

4. Q = (СР)∩(ВD).

5. (АQ)∩(ВР)= М.

Искомая

прямая - (МD)||а.

Задача 3. Даны прямые а || b, точки А, В 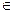а. С помощью линейки удвоить отрезок АВ.

Решение. Так прямые параллельны будем использовать частный случай четырехвершинника – трапецию.

Построение:

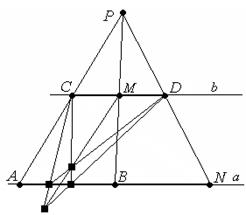
1. На прямой b возьмем две произвольные точки С и D.

2. Используя задачу 1, построим точку М – середину СD.

3. (АС)∩(ВМ)= Р.

4. (РD)∩а = N - искомая точка.