Анализ обмена в двухсубъектной двухпродуктовой экономике
| Коробка Эджуорта |
Коробка Эджуорта (по имени английского экономиста Ф. Эджуорта), представляет совмещенные карты безразличия двух субъектов, А и В, причем карта безразличия В повернута на 180°, так что начала координат каждой из двух карт безразличия становятся противолежащими вершинами прямоугольника (рис. 5.3).

Рис. 5.3. Коробка Эджуорта и контрактная линия
Границы коробки Эджуорта соответствуют фиксированнымколичествам товаров X и Y, находящимся в распоряжении субъектов А и В, так что AL = ВК = ХА + ХB и АK = BL = YA + YB. Количества товаров X и Y фиксированы, потому что в рассматриваемой экономике нет производства, и товары поступают извне.
Любая точка в пределах коробки Эджуорта характеризует некоторое распределение двух товаров, X и Y, между двумя субъектами. Пусть, например, точка S0 на рис. 5.3 будет точкой начального распределения благ X и Y между А и В. Такое распределение товаров S0 субъекты A и В сочтут неудовлетворительным, ведь в точке S0 наклоны пересекающихся здесь кривых безразличия А и В (U0A и U0B) неодинаковы, что означает и неравенство в этой точке их предельных норм замены товаров X и Y. Равновесие потребителей будет точкой касаниякривых безразличия обоих субъектов.
| Контрактная линия |
Множество точек касания кривых безразличия двух субъектов образует так называемую контрактную линию(кривая АВ на рис. 5.3), характеризующую множество взаимоприемлемых результатов обмена двух субъектов. Уравнение контрактной линии имеет вид:
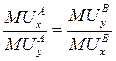 . (5.6)
. (5.6)
Однако не все взаимоприемлемые результаты обмена, принадлежащие контрактной линии, будут одинаково выгодны обоим субъектам. Например, переход из начального распределения товаров S0 к распределению F весь выигрыш от обмена достанется субъекту В, так как субъект А останется на прежней кривой безразличия U0A. Следовательно, участок FG контрактной линии является множеством Парето при распределении запаса товаров.
Добровольный и взаимоприемлемый обмен может иметь своим результатом лишь такое конечное распределение товаров X и Y, которое отображается точками в интервале FG контрактной кривой АВ при исходном распределении S0.
| Пример вывода выражения контрактной линии |
Для степенных функций полезности субъектов 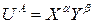 ,
, 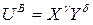 имеем следующее выражение контрактной линии:
имеем следующее выражение контрактной линии:
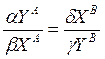 , откуда
, откуда 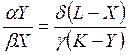 , следовательно
, следовательно
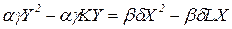 .
.
Обозначив 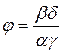 запишем это уравнение в виде:
запишем это уравнение в виде:
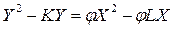 .
.
Это уравнение определяет семейство функций Y=Y(X). Преобразуя к квадрату разности левую и правую части уравнения, получим:
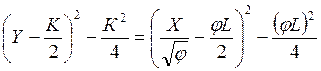 . (5.7)
. (5.7)
Рассмотрим частный случай потребителей, имеющих противоположные предпочтения 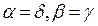 , при этом
, при этом 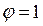 .
.
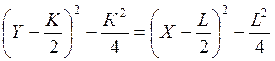 .
.
Для случая равенства запасов K=L имеем:
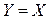 . (5.8)
. (5.8)
Таким образом, контрактная линия является монотонно возрастающей (для степенных функций полезности при равенстве коэффициентов эластичности и одинаковых запасах товаров – линейно возрастающей), то есть при взаимовыгодном обмене увеличение одного товара в запасе должно сопровождаться приростом другого товара.
| Условия максимизации полезности |
Определим, какая именно точка на сегменте FG характеризует конечное распределение товаров X и Y, при котором обмен ими между А и В прекратится. На рис. 5.4 отображены кривые предложения каждого субъекта, ОСА и ОСВ, и две кривые безразличия U0A и U0B. Кривые предложения ОСА и ОСВ пересекаются в некоторой точке Е, поскольку в этой точке касаются кривые безразличия U'A и U'B и бюджетная линия S°E.
Максимальное удовлетворение (полезность) для обоих субъектов возможно в точке касания кривых безразличия субъектов, лежащей на бюджетной линии, проходящей через точку начального запаса товаров:
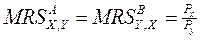 (5.9)
(5.9)
Поскольку из каждой части этого условия было получено выражение кривой предложения для соответствующего субъекта, то равновесие достигается в точке пересечения кривых предложения в коробке Эджуорта, так это точка, через которую проходят наивысшие возможные кривые безразличия при данной бюджетной линии.
| Пример определения равновесия в обмене |
Выражение кривой предложения первого субъекта 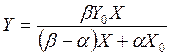 получено выше (формула (5.5)). Выражение кривой предложения второго субъекта найдем, подставив в эту формулу координаты второй системы осей в коробке Эджуорта
получено выше (формула (5.5)). Выражение кривой предложения второго субъекта найдем, подставив в эту формулу координаты второй системы осей в коробке Эджуорта
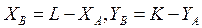 ,
,
и заменив коэффициенты эластичности α на γ, β на δ. В результате получим:
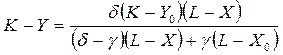 .
.
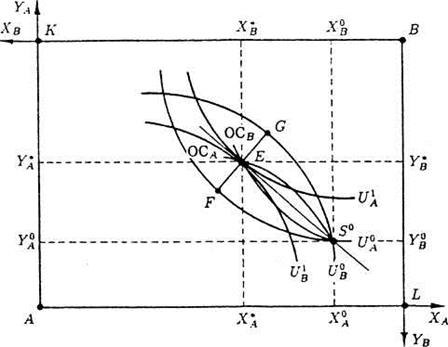
Рис. 5.4. Равновесие в обмене
Координаты точки равновесия определяем, приравнивая выражение кривой предложения первого субъекта и второго субъекта откуда
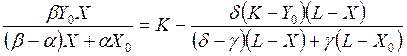 . (5.10)
. (5.10)
Полученное трансцендентное уравнение позволяет определить искомый оптимальный товарный набор.
Поскольку в рассмотренной двухсубъектной экономике простого обмена цены идеальны, то есть при обмене играет роль относительная ценность товаров, обусловленная их количествами в запасах субъектов, то равновесие достигается, притом оно единственно, как точка пересечения монотонных кривых предложения.
§5.4. Равновесие в производстве.
Двухфакторная двухпродуктовая модель
Модель равновесия в производстве аналогична модели равновесия в потреблении, представленной в предыдущем разделе.
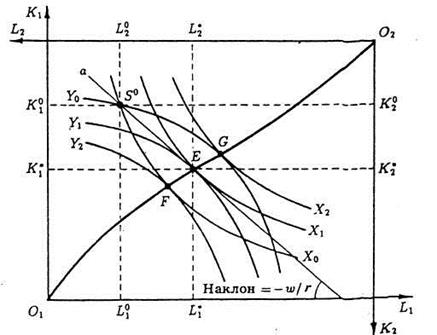
Предположим, что товары X и Y производятся двумя фирмами. В их производстве используются два переменных фактора производства, К и L, приобретаемых по ценам w и r. В коробке Эджуорта производственные функции представлены семействами изоквант. Начальное распределение факторов производства К и L между предприятиями отображается точкой S°. Общее наличие каждого ресурса в экономике фиксировано.
Начальное распределение факторов между предприятиями не удовлетворяет их, так как в точке S° пересекающиеся изокванты Хо и Yо имеют разный наклон и, следовательно, предельные нормы замены факторов оказываются разными. Они будут одинаковы в точках касания изоквант, таких, как F, E, G и множестве других, образующих контрактную кривую О1О2. В любой из них
MRTSXKL = MRTSYKL . (5.11)
|
Рис. 5.5. Равновесие в производстве
Между фирмами начнется обмен ресурсами К и L, который завершится при таком их распределении, которое на рис. 5.5 характеризует точка Е, лежащая на сегменте FG контрактной кривой. Следовательно, в ходе обмена предприятие 1 обменяет часть ресурса К на некоторое количество ресурса L. Достигнуть равновесия в производстве им удастся при соотношении цен факторов w/r, которому соответствует наклон бюджетной линии а на рис. 5.5. Таким образом, равновесие будет при условии:
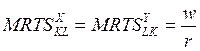 . (5.12)
. (5.12)
По аналогии с результатами предыдущего параграфа, конечное распределение двух факторов производства между фирмами определяется точкой пересечения их кривых предложения, которая в то же время является и точкой касания их изоквант и бюджетной линии, и лежит на контрактной кривой в зоне взаимовыгодного обмена.
Дата добавления: 2020-10-25; просмотров: 959;











