Перевірка гіпотез про числові значення параметрів
Нехай хі (і=1,2,...,п) – значення деякого параметра виробу, що виготовляється станком автоматичної лінії, і нехай а – задане номінальне значення цього параметру. Кожне окреме значення хі може, очевидно, якось відхилятися від заданого номіналу. Очевидно, для того, щоб перевірити правильність налаштування цього станка, потрібно переконатися в тому, що середнє значення параметра у виготовлених на ньому виробів буде відповідати номіналу. Що означає перевірити гіпотезу Н0: 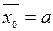 при альтернативній Н1:
при альтернативній Н1: 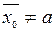 , або Н2:
, або Н2: 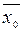 <а, або Н3:
<а, або Н3: 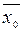 >а.
>а.
При довільному на лаштуванні станка може виникнути необхідність перевірки гіпотези про те, що точність виготовлення виробів по даному параметру, що задана дисперсією 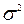 , рівна заданій величині
, рівна заданій величині 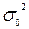 , тобто Н0:
, тобто Н0: 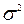 =
= 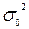 , або наприклад, що частка бракованих виробів, що виготовляються станком, рівна заданій величині р0, тобто Н0:р= р0.
, або наприклад, що частка бракованих виробів, що виготовляються станком, рівна заданій величині р0, тобто Н0:р= р0.
Відповідні критерії перевірки гіпотез про числові значення параметрів нормального закону приведені в таблиці
| Нульова гіпотеза | Припущення | Статистика критерію | Альтернативна гіпотеза | Критерій відхилення гіпотези |
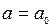
| 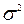 відоме
відоме
| 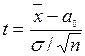
| 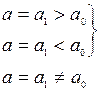
|
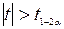
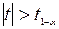
|
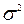 невідоме
невідоме
| 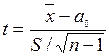
| 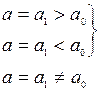
|
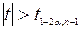
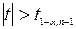
| |
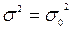
| а невідоме | 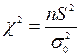
| 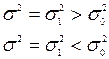
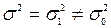
| 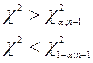 або
або
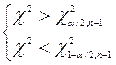
|
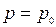
| Достатньо великі п | 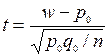
| 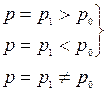
|
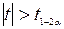
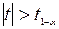
|
Запитання для самоконтролю
1. Що таке статистична гіпотеза? Які є види статистичних гіпотез? Навести приклади статистичних гіпотез.
2. В чому полягають помилки першого та другого роду, які виникають при перевірці гіпотез?
3. Що називають статистичним критерієм перевірки гіпотез? Що таке потужність критерію?
4. Що таке критична область, як її знайти?
5. Яка статистика критерію використовується для перевірки гіпотези про закон розподілу випадкової величини? За якою формулою її обчислюють?
6. Яка статистика критерію використовується для перевірки гіпотези про рівність середніх двох сукупностей? За якою формулою її обчислюють?
7. Яка статистика критерію використовується для перевірки гіпотези про рівність дисперсій двох сукупностей? За якою формулою її обчислюють?
8. Яка статистика критерію використовується для перевірки гіпотези про рівність часток ознаки двох сукупностей? За якою формулою її обчислюють?
9. Що означає перевірити гіпотезу про числові значення параметрів? Навести приклад таких гіпотез?
Тема 10. Елементи теорії кореляції
Кореляційний аналіздосліджує наявність і характер зв’язків між випадковими величинами ознаками генеральної сукупності.
Основна задача кореляційного аналізу полягає у виявленні залежності між випадковими величинами Х та У і може бути розв’язана шляхом побудови статистичних оцінок коефіцієнта кореляції.
Точкову оцінку для коефіцієнта кореляції обчислюють за формулою:
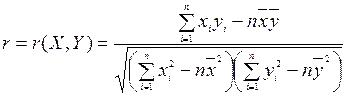 (33)
(33)
Означення. Точкова оцінка 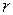 коефіцієнта кореляції між випадковими величинами Х та У. яка обчислюється за формулою (33), називається вибірковим коефіцієнтом кореляції.
коефіцієнта кореляції між випадковими величинами Х та У. яка обчислюється за формулою (33), називається вибірковим коефіцієнтом кореляції.
Вибірковий коефіцієнт кореляції характеризує зв’язок між випадковими величинами Х ті У (ознаками генеральної сукупності):
а) якщо 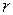 >0, то зв’язок між Х та У є прямий і вони зменшуються або збільшуються одночасно;
>0, то зв’язок між Х та У є прямий і вони зменшуються або збільшуються одночасно;
б) якщо 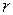 <0, то зв’язок між Х та У є обернений і із збільшенням однієї з них друга зменшується або навпаки;
<0, то зв’язок між Х та У є обернений і із збільшенням однієї з них друга зменшується або навпаки;
в) ) якщо 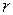 =0, то випадкові величини Х та У є некорельовані і це означає лише відсутність лінійного зв’язку між ними.
=0, то випадкові величини Х та У є некорельовані і це означає лише відсутність лінійного зв’язку між ними.
Вибірковий коефіцієнт кореляції задовольняє нерівність ½ 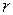 ½≤1.
½≤1.
Нехай потрібно встановити залежність між двома випадковими величинами Х та У. Ці дві випадкові величини можуть бути зв’язані або функціональною залежністю, або так званою статистичною залежністю, або бути незалежними.
Строга функціональна залежність реалізується рідко.
Означення. Статистичною називається залежність, при якій зміна однієї величини викликає зміну розподілу іншої.
Означення. Кореляційною називається статистична залежність, яка проявляється в тому, що при зміні однієї величини змінюється середнє значення іншої.
Причому при кореляційній залежності одному значенню незалежної змінної Х відповідає не одне, а декілька значень залежної змінної У.
Приклад. Нехай Х – випадкова величина, що характеризує вагу людини в кг, а У – відповідний зріст в см і двовимірний статистичний розподіл задається такою таблицею
| У | Х | |||
| п | ||||
| – | – | |||
| – | ||||
| п |
Число, яке лежить на перетині стовпчика хі і рядка уі , вказує частоту, з якою зустрічається пара чисел (хі; уі).
Умовною середньою 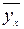 називається середнє арифметичне із значень У, що відповідають одному і тому ж значенню Х=х.
називається середнє арифметичне із значень У, що відповідають одному і тому ж значенню Х=х.
Так, вазі 75 кг відповідає середній зріст
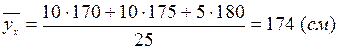 .
.
Аналогічно знаходиться умовна середня 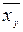 .Очевидно, що умовна середня є функцією х, у цьому випадку говорять, що величина У залежить від Х кореляційно. Використовуючи поняття умовної середньої, введемо таке означення кореляційної залежності.
.Очевидно, що умовна середня є функцією х, у цьому випадку говорять, що величина У залежить від Х кореляційно. Використовуючи поняття умовної середньої, введемо таке означення кореляційної залежності.
Означення. Кореляційною називається залежність умовної середньої 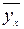 від аргументів х:
від аргументів х: 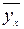 =
= 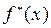 .
.
Якщо є дві і більш змінних то: 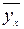 =
= 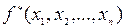 .
.
Рівняння 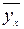 =
= 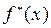 називають рівнянням регресії У на Х, функцію
називають рівнянням регресії У на Х, функцію 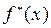 називають регресією У на Х, а її графік – лінією регресії.
називають регресією У на Х, а її графік – лінією регресії.
Найпростішою буде кореляційна залежність, коли є один аргумент. Її називають парною.
Якщо аргументів більше ніж один, то залежність називається множинною.
Вигляд рівняння визначає тип кореляційної залежності.
Найбільш поширеним є рівняння лінійної регресії 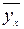 =
= 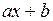 та та квадратичної
та та квадратичної 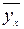 =
= 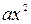 . Відповідно лінії регресії зображені на рис. 8.
. Відповідно лінії регресії зображені на рис. 8.

y=ax+b y=ax2
Рис. 8
Неважко довести, що коефіцієнти рівняння регресії 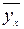 =
= 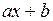 є розв’язками системи рівнянь
є розв’язками системи рівнянь 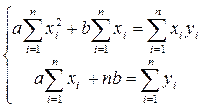 і дорівнюють
і дорівнюють
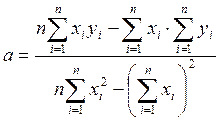 та
та 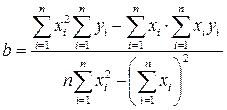 (34)
(34)
А коефіцієнти рівняння 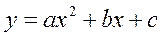 є розв’язком системи рівнянь
є розв’язком системи рівнянь
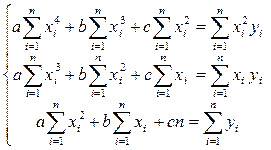 і дорівнюють
і дорівнюють
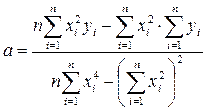 ,
, 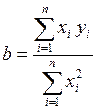 ,
, 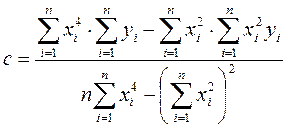
Для знаходження вибіркового рівняння регресії У на Х за даними спостережень використовують метод "натягнутої нитки", методом сум та метод найменших квадратів.
Приклад.Знайти вибіркове рівняння регресії У на Х за даними спостережень: а) методом "натягнутої нитки", б) методом сум, в) методом найменших квадратів. Обчислити коефіцієнт кореляції та дати його тлумачення.
| Х | ||||||||||||||||||||
| У |
Розв’язання
а) метод "натягнутої нитки"
Будуємо кореляційне поле за вибіркою (Х;У):
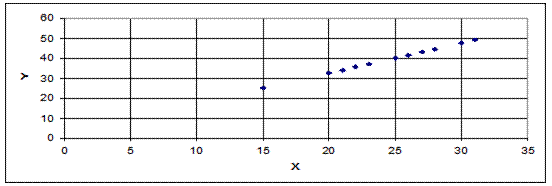
Через точки кореляційного поля проводимо пряму так, щоб в обох півплощинах знаходилася приблизно однакова кількість точок. На цій прямій обираємо дві точки. Наприклад, А(15,25) і В(30,47). Складаємо систему для визначення коефіцієнтів лінійного рівняння залежності між Х та У: y=ax+b. Система буде такою:
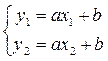
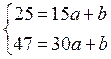
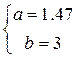 .
.
Отже, рівняння має вигляд: у=1,47х+3
б) метод сум
Умовно ділимо вибірку на дві рівні частини (по 10 елементів). Тоді визначальна система для коефіцієнтів а та b буде такою:
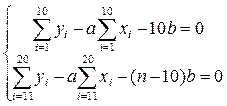
Обчислимо всі суми, які присутні в системі. Розрахунки заносимо в таблицю:
| X | Y | XY | X2 | Y2 | |
| Сума | |||||
| Сума | |||||
| Загальна сума |
Тоді система набуває вигляду:
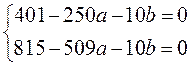
 .
.
Відповідне рівняння у=1,6х+0,1.
в) метод найменших квадратів
Визначальна система для коефіцієнтів рівняння така:
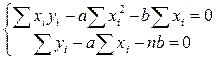
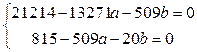
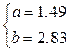
Відповідне рівняння у=1,49х+2,83.
Коефіцієнт кореляції обчислюємо за формулою:
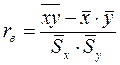
Проміжні обчислення:
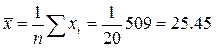 ;
; 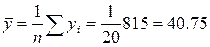 ;
; 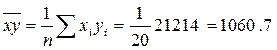
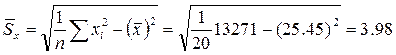 ,
, 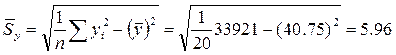
Тоді 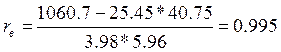 .
.
Оскільки коефіцієнт кореляції дуже близький до 1, то залежність між Х та У можна вважати лінійною.
Приклад. Зв’язок між кількісними ознаками Х та У генеральної сукупності задається таблицею
| Х | ||||||||||
| У |
Записати рівняння прямої регресії У на Х.
Розв’язання
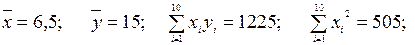
Скористаємося формулами (34) для знаходження коефіцієнтів лінійної регресії. отримаємо а=3,03, b=-4,70.
Отже вибіркове рівняння регресії: у=3,03х-4,7.
Щоб переконатися в тому, що наше припущення про лінійність зв’язку між Х та У було правильним, обчислимо вибірковий коефіцієнт кореляції за формулою (33), отримаємо
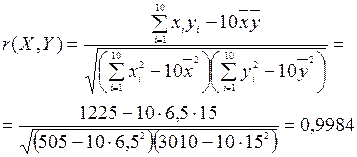
Оскільки вибірковий коефіцієнт кореляції 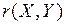 є досить близьким до одиниці, то припущення про лінійність зв’язку між Х та У – правильне. Крім цього, зв’язок є додатний і ці величини збільшуються одночасно.
є досить близьким до одиниці, то припущення про лінійність зв’язку між Х та У – правильне. Крім цього, зв’язок є додатний і ці величини збільшуються одночасно.
Запитання для самоконтролю
1. Що досліджує кореляційний аналіз? Яка його основна задача?
2. Як обчислюється вибірковий коефіцієнт кореляції та що він характеризує?
3. Що таке статистична та кореляційна залежність?
4. Що називають умовною середньою?
5. Які існують методи побудови рівняння залежності? В чому їх сутність?
Тема 11. Поняттядисперсійного аналізу. Однофакторний дисперсійний аналіз
Дисперсійний аналіз – це метод порівняння декількох (більше 2-х) вибірок за властивістю, що виміряна з допомогою метричної шкали*. Загальноприйняте скорочення дисперсійного аналізу – (ANOVA)**. Як і у випадку порівняння двох вибірок за допомогою критерію Стьюдента, ANOVA розв’язує задачу порівняння середніх значень, але не двох, а декількох вибірок. Крім того метод допускає порівняння вибірок більш ніж за однієї основи – коли розподіл на вибірки відбувається по декількох змінних, кожна з яких має дві і більше градації. Наприклад, досліджється вплив на продуктивність відтворення вербального матеріалу (У): а) інтервал між 5-ти повтореннями (Х1–3 градації: 1–0хв., 2 – 3хв., 3 – 10хв.) б) складність матеріалу ( Х2 – 2 градації: 1 – легкий, 2 – складний).
Структура даних
| № | Х1 | Х2 | У |
| ... | ... | … | ... |
| N |
Означення. ANOVA – статистичний метод, за допомогою якого оцінюють вплив різних факторів на результат експерименту, а також для подальшого планування аналогічних експериментів.
ANOVA розробив у 1918 році англійський математик-статист Р.А. Фішер для обробки результатів агрономічних дослідів по вияву умов отримання максимального врожаю різних сортів сільськогосподарських культур.
Типова схема експерименту зводиться до вивчення впливу незалежної змінної (однієї або кількох) на залежну змінну. Незалежна змінна являє собою якісно визначену (номінативну) властивість, що має 2 або більше градацій. Кожній градації незалежної змінної відповідає вибірка об’єктів (досліджуваних), для яких визначені значення залежної змінної. Незалежну змінну називають фактором, що має декілька градацій (рівнів). Залежна змінна в експериментальному дослідженні розглядається як така, що змінюється під впливом факторів.
В залежності від співвідношення вибірок, що відповідають різним рівням фактора, розрізняють два види факторів: міжгруповий – при незалежних вибірках; внутрішньогруповий – при залежних вибірках. По числу факторів, вплив яких досліджується, розрізняють однофакторний і багатофакторний дисперсійний аналіз.
Означення. Однофакторний ANOVA – статистичний метод, що використовується при вивченні впливу одного фактору на залежну змінну.
Означення. Багатофакторний ANOVA – статистичний метод, що використовується при вивченні впливу двох і більше фактору на залежну змінну.
Багатофакторний ANOVA дозволяє перевіряти гіпотезу не тільки про вплив кожного фактора окремо, а й про взаємозв’язок факторів.
Приклад. Припустимо вивчається вплив на глядацьку оцінку різних фільмів (залежна змінна) двох факторів: жанру фільму та статі глядача. Цілком ймовірно, що в результаті такого дослідження будуть виявлені не головні ефекти досліджуваних факторів (вплив кожного з них окремо), а їх взаємодію, тобто що чоловіки і жінки по-різному оцінюють фільми в залежності від їх жанру.
Надалі будемо розглядати однофакторний ANOVA.
Однофакторний ANOVA дозволяє перевірити гіпотезу про те, що досліджуваний фактор чинить вплив на залежну змінну (середні значення, що відповідають різним рівням фактора, різні).
Математична модель однофакторногоANOVA передбачає виділення в загальній мінливості залежної змінної двох її складових: міжгрупова (факторна) складова мінливості обумовлена різницею середніх значень під впливом фактору; внутрішньогрупова (випадкова) складова мінливості обумовлена впливом неврахованих причин. співвідношення першої і другої складової і є основним показником, що визначає статистичну значимість впливу фактора.
Нульова статистична гіпотеза містить твердження про рівність середніх значень. При її відхиленні приймається альтернативна гіпотеза про те, що принаймні два середні значення відрізняються.
Вихідні припущення розподіл залежної змінної в порівнюваних генеральних сукупностях характеризується нормальним законом і однаковими дисперсіями. вибірки є випадковими і незалежними. Перевірка вихідних припущень зводиться до перевірки однорідності дисперсій в порівнюваних вибірках у випадку, якщо вони помітно різняться об’ємами.
Структура вихідних даних досліджувана властивість виміряна на об’єктів, кожен з яких належить до однієї з декількох порівнювальних вибірок.
Обмеження: якщо дисперсії вибірок відрізняються статистично достовірно, то метод не застосовують. Фактично необхідно мати не менше 5 об’єктів в кожній вибірці.
Основний результат: прийняття чи відхилення статистичної гіпотези про рівність середніх значень, що відповідають різним рівням фактора. Основний показник для прийняття рішення – р-рівень значимості критерію F-Фішера.
Розглянемо загальні принципи і послідовність обчислення для однофакторного дисперсійного аналізу у випадку рівних об’ємів порівняльних вибірок.
Вихідна ідея заключається у спроможності розкладання показника мінливості в середині груп і мінливість між групами. В якості показника мінливості використовується сума квадратів відхилення значень ознаки від середнього, що позначається SS.
Загальна сума квадратів SSзаг є показником загальної мінливості залежної змінної і являє собою чисельник дисперсії
SSзаг= 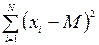
Відповідно, загальна сума квадратів рівна сумі міжгрупової і внутрішньогрупової суми квадратів: SSзаг= SSвг+ SSмг
Міжгрупова SSмг – показник мінливості між k групами (кожна чисельністю п об’єктів): SSмг= 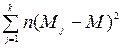 , де
, де 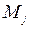 – середні значення для груп j.
– середні значення для груп j.
Відношення міжгрупової і загальногрупової суми квадратів показує долю загальної дисперсії залежної змінної, що обумовлена впливом фактора
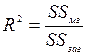 – коефіцієнт детермінації, 0£
– коефіцієнт детермінації, 0£ 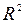 £1
£1
Чим більший 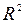 , тим більший вплив досліджуваного фактора на дисперсію залежної змінної.
, тим більший вплив досліджуваного фактора на дисперсію залежної змінної.
Внутрішньогрупова сума квадратів SSвг – показник випадкової мінливості
SSвг= SSзаг- SSмг= 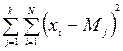
На величину сум квадратів впливає об’єм і кількість порівняльних груп. Тому для співвідношення міжгрупової і внутрішньогрупової мінливості використовуються середні квадрати MS.
Означення. Середній квадрат – це частка від ділення суми квадратів на відповідне число ступенів вільності.
Кожна сума квадратів характеризується своїм числом ступенів вільності df. Так, загальне число ступенів вільності відповідає загальній сумі квадратів і рівне: dfзаг=N-1.
Відповідно: dfмг=k-1; dfвг=N-k.
Після визначення числа ступенів вільності обчислюють середні квадрати 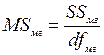 – міжгруповий середній квадрат;
– міжгруповий середній квадрат;
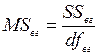 – внутрішньогруповий середній квадрат.
– внутрішньогруповий середній квадрат.
Основним показником ANOVA є F-відношення – емпіричне значення критерію F-Фішера:
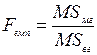
Процедура перевірки Н0 має наувазі направлену альтернативу, так як її відхиленню відповідає тільки більше значення 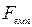 . тому для визначення р-рівня значимості при обчисленнях застосовують таблиці критичних значень F-розподілу для направлених альтернатив (односторонній критерій). Для одних і тих же df рівень значимості зростає (р-рівень спадає) при зростанні
. тому для визначення р-рівня значимості при обчисленнях застосовують таблиці критичних значень F-розподілу для направлених альтернатив (односторонній критерій). Для одних і тих же df рівень значимості зростає (р-рівень спадає) при зростанні 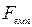 .
.
Приклад. Досліджується різниця в продуктивності відтворення одного і того ж матеріалу трьох груп досліджуваних (по 5 чоловік), що відрізняються умовами представлення цього матеріалу для запам’ятовування. Залежна змінна (У) – кількість відтворених одиниць матеріалу, незалежна змінна (фактор) – умови представлення (три градації). Перевіримо на рівні a=0,01 гіпотезу про те, що продуктивність відтворення матеріалу залежить від умов його представлення.
| Умова 1 | Умова 2 | Умова 3 | |||
| № | У | № | У | № | У |
Розв’язання
Загальна середня М=7
Середня для різних умов: М1=5, М2=7, М2=9
1. SSзаг= 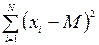 =
= 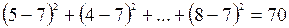 ;
;
SSмг= 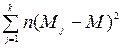 =
= 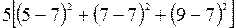 ;
;
SSвг= SSзаг- SSмг= 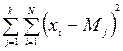 70-40=30
70-40=30
2. 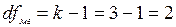 ;
; 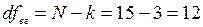 ;
;
3. 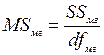 =
= 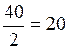 ;
;
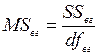 =
= 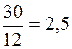 ;
;
4. 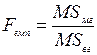 =
= 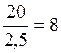 .
.
5. Визначимо р-рівень значимості. За табл. критичних точок F-розподілу для р=0,01 та 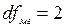 ,
, 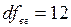 Fкрит.=6,927. Відповідно, р<0,01.
Fкрит.=6,927. Відповідно, р<0,01.
Обчислимо коефіцієнт детермінації: 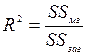 =
= 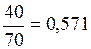 .
.
6. Відхиляємо гіпотезу Н0 і приймаємо альтернативну гіпотезу про те, що міжгрупова мінливість більша внутрішньогрупової ( 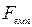 >Fкрит.).
>Fкрит.).
Змістовний висновок: виявлено статистично достовірний вплив умов представлення матеріалу на продуктивність його відтворення (р<0,01). Або: середні значення продуктивності відтворення матеріалу статистично достовірно відрізняються в залежності від умов його представлення
Запитання для самоконтролю
1. Що означає провести дисперсійний аналіз? Назвати його види.
2. Яка математична модель однофакторного дисперсійного аналізу?
3. Як формулюється нульова статистична гіпотеза при однофакторному дисперсійному аналізі?
4. Які вихідні припущення при однофакторному дисперсійному аналізі?
5. Які обмеження на застосування однофакторного дисперсійного аналізу?
6. Що є основним результатом однофакторного дисперсійного аналізу?
7. Назвати загальні принципи та вкажіть послідовність обчислення для однофакторного дисперсійного аналізу у випадку рівних об’ємів порівняльних вибірок.
8. Що таке коефіцієнт детермінації, його зміст та формула обчислення.
Практичні заняття
Практичне заняття № 15-16 (4 год)
Тема: Перевірка статистичних гіпотез.
Мета: сформувати у студентів уявлення про статистичні гіпотези, навчити обчислювати статистики, знаходити критичні області, застосовувати критерії прийняття нульової та альтернативної гіпотез.
План Заняття
1. Статистичні гіпотези та їх різновиди. Похибки перевірки гіпотез.
2. Статистичний критерій перевірки нульової гіпотези. Основні принципи побудови критичної області.
3. Перевірка гіпотези про нормальний закон розподілу генеральної сукупності. Критерій згоди Пірсона.
4. Перевірка гіпотези про рівність середніх двох нормальних генеральних сукупностей при відомих та невідомих дисперсіях.
5. Перевірка гіпотези про рівність дисперсій двох нормальних генеральних сукупностей.
6. Перевірка гіпотези про рівність часток ознаки двох нормальних генеральних сукупностей.
7. Перевірка гіпотез про числові значення параметрів.
Рекомендована Література
1. Теорія ймовірностей та математична статистика: Навч. посібник для студентів вузів/ В.В. Барковський, Н.В. Барковська Н.В., О.К. Лопатін. 3-є вид. перероб. і доп.– К.: Центр навчальної літератури, 2002. С. 249-264.
2. Математика для психологов: Учебник /А.Н. Киричевец, Е.В. Шикин, А.Г. Дьячков / Под ред. А.Н. Киричевца. – М.:Флинта: Московский психолого-социальный институт, 2003. С.343-365.
3. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ Н.Ш. Кремер. -3-е изд., перераб. и доп.- М.: Юнити, 2007. – С. 330-379.
4. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. –М.: Даликов и К, 2008. –С-268-310.
5. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов/Ред. В.И. Єрмаков –М. Инфра-М,2008–С.98-101.
6. Теория вероятностей и математическая статистика: примеры и задачи: Учебное пособие для студентов вузов/ И.В. Белько, Г.П. Свирид. -3-е изд., стереотип.–М.: Новое знание, 2007.С.144-150.
7. Посібник з теорії ймовірності та математичної статистики: Навч. посібник для вузів/ М. К. Бугір. – Тернопіль: Підручники і посібники, 1998. –С.114-118.
8. Основи теорії ймовірностей та математичної статистики: Навчальний посібник для студентів/ В.П. Бабак, А.Я. Білецький, О.П. Приставка, П.О. Приставка.-К.: КВІЦ.,2003. –С.284-298.
9. Математична статистика: Навчальний посібник для студентів вузів/ В.К. Гаркавий, В.В. Ярова. –К.: Профессионал, 2004. –С. 137-147.
10. Статистика (з програмованою формою контролю знань): математична статистика. Загальна теорія статистики: Навчальний посібник для студентів вузів/ А.Т. Опря. -К.: Центр навчальної літератури, 2005. –С. 129-134.
11. Практикум з математичної статистики: Навчальний посібник для студентів вузів/ А.Т. Мармоза. –К.: Кондор, 2004. –С. 101-148.
12. Математические методы психологического исследования. Анализ и интерпретация данных. Учебное пособие. 3-е изд., / Наследов А.Д. –СПб.: Речь, 2007. – С.93-146.
Методичні вказівки
При підготовці даної теми вивчити означення таких понять як статистична гіпотеза, нульова гіпотеза, альтернативна (конкуруюча) гіпотеза, статистичний критерій, критична область, область прийняття гіпотези, критична точка. Знати у чому полягають помилки першого та другого роду, які можуть бути зроблені при перевірці гіпотез. Звернути увагу на односторонню (правосторонню, лівосторонню) та двосторонню критичні області, вміти їх будувати на числовій прямій. Вміти знаходити критичні точки за таблицями різних розподілів. Вивчити алгоритми перевірки та умови прийняття нульової гіпотези при різних варіантах альтернативних гіпотез при перевірці гіпотез, що зазначені у плані заняття.
задачі для самоконтролю
Задача 1. При рівні значущості 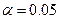 перевірити гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні і теоретичні частоти
перевірити гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні і теоретичні частоти
| Емпіричні частоти | ||||||||
| Теоретичні частоти |
Відповідь: розбіжність емпіричних та теоретичних частот незначуща. Отже, генеральна сукупність розподілена нормально.
Задача 2.За двома незалежними вибірками обсягу 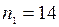 і
і 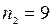 знайдені середні розміри деталей відповідно
знайдені середні розміри деталей відповідно 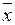 =182мм і
=182мм і 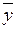 =185мм, виготовлених на першому і другому автоматах. Встановлено, що розмір деталі, виготовленої кожним автоматом, має нормальний закон розподілу. Відомі дисперсії
=185мм, виготовлених на першому і другому автоматах. Встановлено, що розмір деталі, виготовленої кожним автоматом, має нормальний закон розподілу. Відомі дисперсії 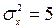 і
і 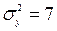 для першого і другого автоматів. На рівні значимості 0,05 виявити вплив на середній розмір деталі автомату , на якому вона виготовлена. Розглянути два випадки: а)
для першого і другого автоматів. На рівні значимості 0,05 виявити вплив на середній розмір деталі автомату , на якому вона виготовлена. Розглянути два випадки: а) 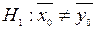 ; б)
; б) 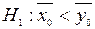 . Відповідь: а) вплив суттєвий, оскільки t=2,82>t0.95=1,96 (двохсторонній критерій); б) вплив суттєвий, оскільки t=2,82>t0.9=1,64.
. Відповідь: а) вплив суттєвий, оскільки t=2,82>t0.95=1,96 (двохсторонній критерій); б) вплив суттєвий, оскільки t=2,82>t0.9=1,64.
Задача 3. За двома незалежними вибірками обсягу 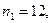
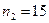 вибраним з генеральних сукупностей Х та У, знайдені виправлені вибіркові дисперсії
вибраним з генеральних сукупностей Х та У, знайдені виправлені вибіркові дисперсії 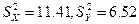 . Перевірити нульову гіпотезу
. Перевірити нульову гіпотезу 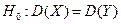 про рівність генеральних дисперсій при альтернативній гіпотезі а)
про рівність генеральних дисперсій при альтернативній гіпотезі а) 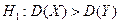 при рівні значущості
при рівні значущості 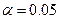 ; б)
; б) 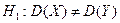 при рівні значущості
при рівні значущості 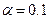 .
.
Відповідь: а) немає підстав відхиляти нульову гіпотезу про рівність дисперсій генеральних дисперсій. б) немає підстав відхиляти нульову гіпотезу про рівність дисперсій генеральних дисперсій.
Задача 4. За вибіркою об’єму n=20 знайдено виправлену дисперсію 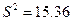 . При рівні значущості
. При рівні значущості 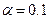 перевірити нульову гіпотезу
перевірити нульову гіпотезу 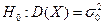 про рівність дисперсії гіпотетичному значенню при альтернативній гіпотезі а)
про рівність дисперсії гіпотетичному значенню при альтернативній гіпотезі а) 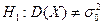 ; б)
; б) 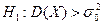 ; в)
; в) 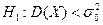 , якщо
, якщо 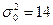 .
.
Відповідь: а) немає підстав відхиляти нульову гіпотезу; б) приймаємо нульову гіпотезу; в) приймаємо нульову гіпотезу.
Задача 5. Вступний екзамен проводився на двох факультетах університету. На природничому факультеті із n1=900 абітурієнтів склали екзамен 500 чоловік; а на психолого-педагогічному факультеті із n1=800 абітурієнтів склали екзамен 408 чоловік. на рівні значимості 0,05 перевірити гіпотезу про відсутність суттєвої різниці в рівні підготовки абітурієнтів для двох факультетів. Розглянути два випадки: а) 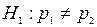 ; б)
; б) 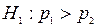 .
.
Дата добавления: 2022-02-05; просмотров: 654;











