Математична довідка

І. Факторіал натурального числа n – це добуток натуральних чисел від одиниці до n включно, позначається n!.

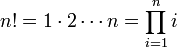За означенням 0! = 1.

Зауваження. При великих n наближене значення факторіала можна обчислити за формулою Стірлінга, яка є наближенням для великих факторіалів та названа на честь Джеймса Стірлінґа. Формально, вона твердить, що

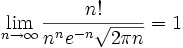
або

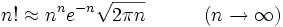
Факторіал n дорівнює кількості перестановок з n елементів.

0! = 1
1! = 1
2! = 1·2 = 2
3! = 1·2·3 = 6
4! = 1·2·3·4 = 24
5! = 1·2·3·4·5 = 120

6! = 1·2·3·4·5 ·6= 720

7! = 1·2·3·4·5 ·6·7= 5040

8! = 1·2·3·4·5 ·6·7·8= 40320

9! = 1·2·3·4·5 ·6·7·8·9= 362880

10! = 1·2·3·4·5 ·6·7·8·9·10= 3628800

ІІ. е —математична константа, основа натурального логарифма, ірраціональне і трансцедентне число. Інколи число e називають числом Ейлера або Неперовим числом. Воно грає важливу роль в диференціальному та інтегральному численні, а також багатьох інших розділах математики.

2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274 27466 …

Число e може бути визначене декількома способами:

Через границю:

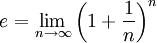(друга чудова границя).

Як сума ряду:

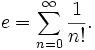
Як єдине число a, для якого виконується

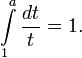
Як єдине додатне число a, для якого вірно

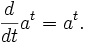
ІІІ. Функція

Якщо кожному значенню змінної х, що належить деякiй областi вiдповiдає одне певне значення другої змінної y, то y є функція від х, або в символічному записі, y = f(x), y = φ (x) i т.п.

х – називається незалежною змінною або аргументом.

Сукупність значень х, для котрих визначається значення функції y в силу правила f(x), називається областю визначення функції (або областю iснування функції).

Iнодi в означеннi функції допускають, що кожному значенню х, належному деякій області, вiдповiдає не одне, а декілька значень y. В цьому випадку функцію називають многозначною.

<52 53 54 55 565758 >

Дата добавления: 2022-02-05; просмотров: 250;

Поиск по сайту

Узнать еще