Перевірка гіпотези про рівність дисперсій двох сукупностей

Гіпотези про дисперсії виникають доволі часто, оскільки дисперсія характеризує такі виключно важливі показники, як точність машини, приладу, технологічних процесів, ступінь однорідностей сукупностей і т.і.

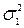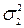Сформулюємо задачу. Нехай маємо дві нормально розподілені сукупності, дисперсії яких рівні і . Необхідно перевірити нульову гіпотезу про рівність дисперсій, відносно конкурентної Н₁: 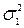> 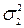або Н₂: 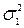¹ .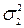

Для перевірки гіпотези Н₀із цих сукупностей взяли дві незалежні вибірки об’ємами п₁ і п₂. Для оцінки дисперсій 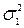і 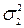використаємо виправлені вибіркові дисперсі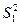ї і 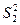. Звідси, задача перевірки гіпотези зводиться до порівняння дисперсій 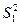і .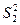

Доведено, що випадкова величина F, що визначається відношенням:

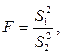(32)

має F- розподіл Фішера-Снедекора з k₁=n₁-1 і k₂=n₂-1 ступенями вільності.

Слід мати на увазі, що F-розподіл Фішера-Снедекора є несиметричним, тому гіпотеза Н₀ відхиляється, якщо F>F_a,k1;k2 (у випадку правосторонньої критичної області) або F<F_1-a/2,k1;k2 чи F>F_a/2,k1;k2 (у випадку двосторонньої критичної області). У протилежному випадку гіпотеза Н₀ приймається.

Приклад. На двох токарних станках обробляються деталі. Відібрані дві проби: із деталей, зроблених на першому станку, п₁=15шт., на другому п₂=18шт. Поданих цих вибірок розраховані вибіркові дисперсі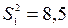ї і 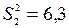відповідно. Припускаючи, що розміри деталей підпорядковуються нормальному закону розподілу, на рівні значимості a=0,05 з’ясувати, чи можна вважати, станки володіють різною точністю.

Розв’язання

Припустимо, що дисперсії розмірів деталей, що оброблялися кожним станком рівні, тобто Н₀: 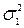= 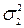. Тоді Н₁: 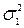> 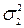(дисперсія першого більша).

За формулою (32) маємо 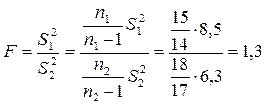(в якості дисперсії 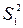беруть більшу із двох дисперсій).

За таблицею критичних значень F-Фішера (додаток 6) при рівні значимості a=0,05 та k₁=п₁-1=14 і k₂=п₂-1=17 знаходимо критичне значення, тобто F_кр=F_{0,05; 14;17}=2,33. Оскільки F< F_кр, то гіпотеза Н₀ не відхиляється.

Зауваження. Якщо Н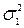₁: ¹ 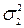, то слід знайти F_1-a/2;k1;k2 і F_a/2;k1;k2, Оскільки за таблицею можна знайти лише праву границю, то ліву знаходять із співвідношення, доведеного для F-критерію: F_{1‑a/2;k1;k2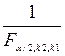}= . У даному випадку при a=0,05 в задачі потрібно знайти F_0,025;14;17 і F_0,975;14;17= .

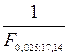Приклад . За рівнем значущості a=0,05 порівняти вагу семимісячних немовлят двох груп (перша група мала штучне вигодовування, а друга – грудне), якщо за вибірками одержали такі показники

п₁=20; 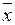=8,0; S_x=0,3

п₂=25; 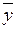=8,6; S_у=0,4

Розв’язання

За рівнем значущості a=0,05 перевіримо гіпотезу про рівність середніх Н₀: 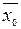= 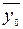, при альтернативній гіпотезі Н₁: < .

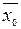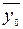Спочатку перевіримо гіпотезу про рівність дисперсій 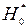: s²_х=s²_у при альтернативній гіпотезі 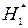: s²_х> s²_у .

Обчислимо значення критерію за формулою (32) .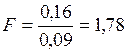

За таблицею критичних значень розподілу Фішера (додаток 6) для a=0,05 і кількості ступенів вільності к₁=25-1=24, к₂=20-1=19, знаходимо критичну точку F_кр. =2,11.

Оскільки F < F_кр. , то 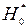:s²_х=s²_у приймаємо і нема підстав відхиляти гіпотезу про рівність середніх.

Обчислимо спостережуване значення статистики за формулою (31):

t=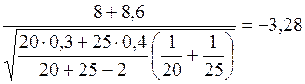

За таблицею критичних значень розподілу Стьюдента (додаток 5) для a=0,05 і кількості ступенів вільності к=20+25-2=43 знаходимо критичну точку розподілу Стьюдента t_кр. =2,02.

Оскільки ½t½>t_кр., то гіпотезу про рівність середніх відхиляємо. Тобто середня вага немовлят, що росли на штучному харчуванні менша ніж середня вага немовлят, що вигодовувалися грудним молоком.