Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
Пусть дана функциональная последовательность 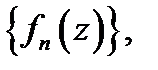 состоящая из комплексных функций (
состоящая из комплексных функций ( 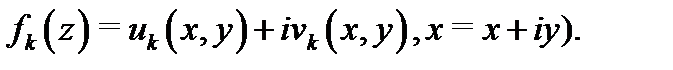 Тогда формальная сумма бесконечного числа слагаемых:
Тогда формальная сумма бесконечного числа слагаемых:
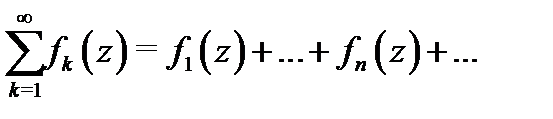
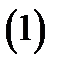
называется рядом, построенным по указанной функциональной последовательности. В частности, если все 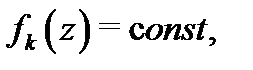 то ряд будет числовым. При этом
то ряд будет числовым. При этом 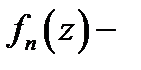 общий член ряда (1), а
общий член ряда (1), а 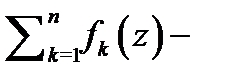 его
его 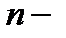 я частичная сумма. Множество
я частичная сумма. Множество
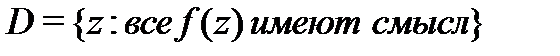
называется областью определения ряда (1).
Определение 1.Говорят, что ряд (1) сходится в точке 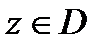 к сумме
к сумме 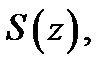 если существует конечный предел
если существует конечный предел 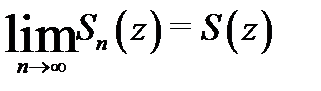 его частичных сумм. Это эквивалентно высказыванию
его частичных сумм. Это эквивалентно высказыванию 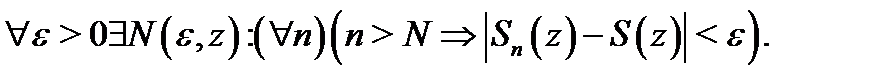 Если здесь номер
Если здесь номер 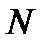 не зависит от
не зависит от 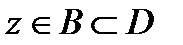 (т.е.
(т.е. 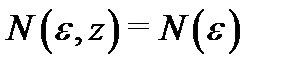 ), то говорят, что ряд (1) сходится равномерно по
), то говорят, что ряд (1) сходится равномерно по 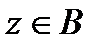 (или равномерно на множестве
(или равномерно на множестве 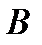 ).
).
Это определение фактически не отличается от аналогичного определения в действительном анализе. Поэтому здесь также справедливы следующие утверждения.
1. Если ряд (1) сходится в точке 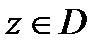 , то его общий член
, то его общий член 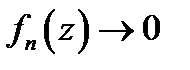 при
при 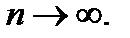
2. Если ``модульный ряд'' 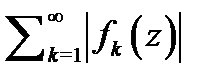 сходится, то сходится и сам ряд (1) (в этом случае говорят, что ряд (1) сходится абсолютно; если ряд (1) сходится, а его ``модульный ряд'' расходится, то говорят, что (1) сходится условно).
сходится, то сходится и сам ряд (1) (в этом случае говорят, что ряд (1) сходится абсолютно; если ряд (1) сходится, а его ``модульный ряд'' расходится, то говорят, что (1) сходится условно).
Для нахождения области абсолютной сходимости ряда (1) и области его равномерной сходимости надо применить известные признаки сходимости (Даламбера, Коши, интегральный признак, признак Вейерштрасса) к действительному знакоположительному ряду 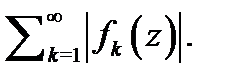 При этом все свойства равномерно сходящихся действительных рядов рядов переносятся и на комплексные ряды. Эти свойства следующие.
При этом все свойства равномерно сходящихся действительных рядов рядов переносятся и на комплексные ряды. Эти свойства следующие.
3. Если ряд (1) состоит из непрерывных на множестве 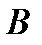 слагаемых
слагаемых 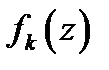 и сходится к сумме
и сходится к сумме 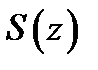 равномерно на множестве
равномерно на множестве 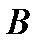 , то его сумма
, то его сумма 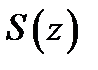 непрерывна на
непрерывна на 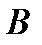 .
.
4. Если ряд (1) сходится равномерно на ограниченной кусочно- гладкой кривой 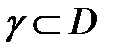 и все его члены непрерывны на
и все его члены непрерывны на 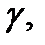 то ряд (1) можно интегрировать на
то ряд (1) можно интегрировать на 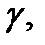 т.е.
т.е.
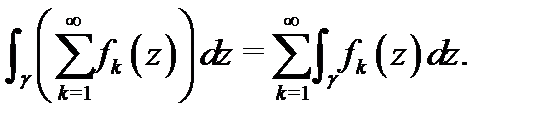
5. Если все члены ряда (1) аналитичны в ограниченной односвязной области 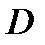 и ряд (1) сходится равномерно в замкнутой области
и ряд (1) сходится равномерно в замкнутой области  то его сумма
то его сумма 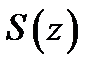 аналитична в
аналитична в 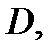 причем
причем
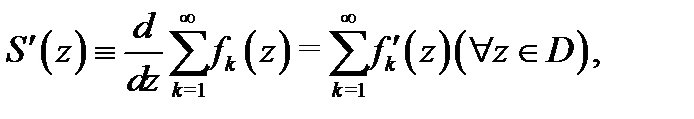
а ряд из производных будет сходиться равномерно по 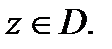
1. Степенные ряды. Ряды Тейлора и Лорана
Функциональные ряды вида 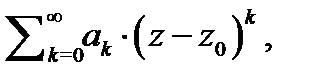 где
где 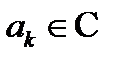 (коэффициенты ряда) и
(коэффициенты ряда) и 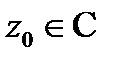 (центр ряда) – постоянные,
(центр ряда) – постоянные, 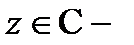 переменная, называются степенными рядами. Ясно, что если мы научимся вычислять область сходимости степенного ряда
переменная, называются степенными рядами. Ясно, что если мы научимся вычислять область сходимости степенного ряда
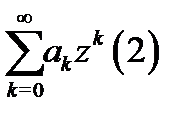
(с центром 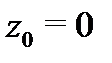 ), то легко найдем и область сходимости исходного ряда
), то легко найдем и область сходимости исходного ряда 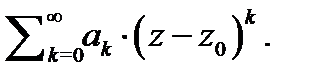 Поэтому впредь, если не оговорено противное, будем рассматривать степенные ряды
Поэтому впредь, если не оговорено противное, будем рассматривать степенные ряды 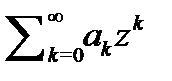 .
.
Теорема Абеля.Если степенной ряд 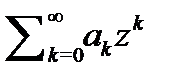 сходится в точке
сходится в точке 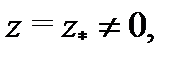 то он сходится абсолютно и в круге
то он сходится абсолютно и в круге 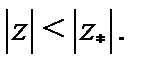 В любом замкнутом круге
В любом замкнутом круге 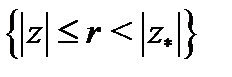 указанный ряд сходится равномерно.
указанный ряд сходится равномерно.
Так же, как и в действительном анализе, здесь вводится понятие радиуса сходимости ряда.
Определение 2. Число 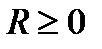 называется радиусом сходимости ряда (2), если внутри круга
называется радиусом сходимости ряда (2), если внутри круга 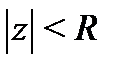 этот ряд сходится абсолютно, а вне замкнутого круга
этот ряд сходится абсолютно, а вне замкнутого круга 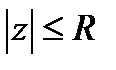 он расходится. При этом круг
он расходится. При этом круг 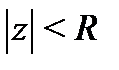 называется кругом сходимости ряда
называется кругом сходимости ряда 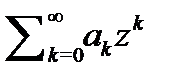 .
.
Заметим, что при 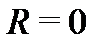 указанный степенной ряд сходится только в точке
указанный степенной ряд сходится только в точке 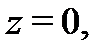 а при
а при 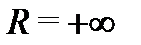 он сходится при всех комплексных
он сходится при всех комплексных 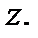 Следующие примеры показывают, что эти случаи не исключаются:
Следующие примеры показывают, что эти случаи не исключаются: 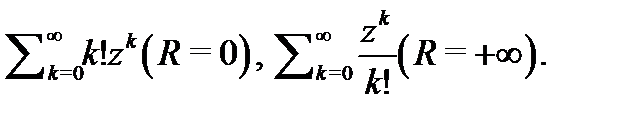 Примером ряда с ненулевым конечным радиусом сходимости может служить геометрическая прогрессия
Примером ряда с ненулевым конечным радиусом сходимости может служить геометрическая прогрессия 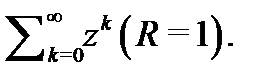 Заметим также, что на границе
Заметим также, что на границе 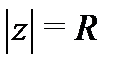 круга сходимости степенной ряд может как сходиться, так и расходиться. Например, ряд
круга сходимости степенной ряд может как сходиться, так и расходиться. Например, ряд 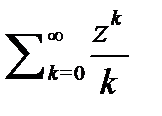 сходится условно в точке
сходится условно в точке 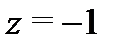 и расходится в точке
и расходится в точке 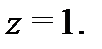
Здесь так же, как и в действительном анализе имеет место утверждение.
Теорема 1. Пусть выполнено хотя бы одно из следующих условий:
а) существует (конечный или бесконечный) предел 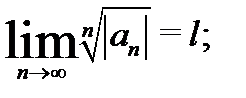
б) существует (конечный или бесконечный) предел 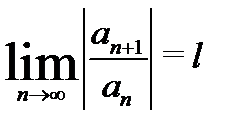 (при этом предполагается, что существует номер
(при этом предполагается, что существует номер 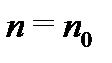 такой, что
такой, что 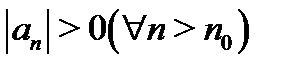 ).
).
Тогда число 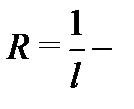 радиус сходимости ряда
радиус сходимости ряда 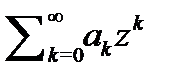 .
.
Пусть функция 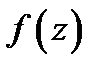 имеет в точке
имеет в точке 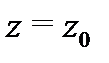 и некоторой её окрестности
и некоторой её окрестности 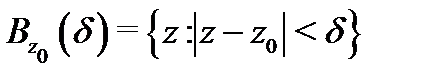 производные
производные 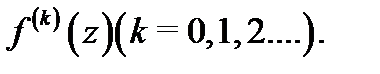 Тогда этой функции можно поставить в соответствие степенной ряд
Тогда этой функции можно поставить в соответствие степенной ряд
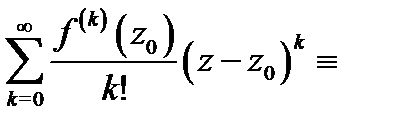
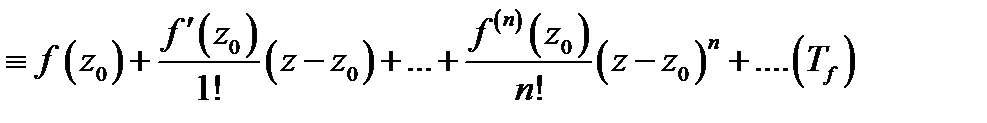
Этот ряд называется рядом Тейлора, построенным по функции 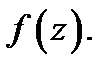 Возникают следующие естественные вопросы:
Возникают следующие естественные вопросы:
1) при каких условиях на функцию 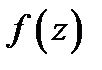 ряд
ряд 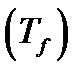 сходится и какова область его сходимости?
сходится и какова область его сходимости?
2) при каких условиях на функцию 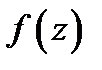 ряд
ряд 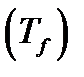 сходится именно к функции
сходится именно к функции 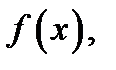 по которой он строится?
по которой он строится?
На первый вопрос можно ответить, применяя к 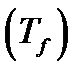 признаки сходимости степенных
признаки сходимости степенных
рядов. Ответ на второй вопрос содержится в следующем утверждении.
Теорема 2 (о разложимости аналитической функции в ряд Тейлора). Пусть функция 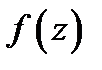 аналитична в области
аналитична в области 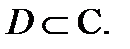 Тогда в любом круге
Тогда в любом круге 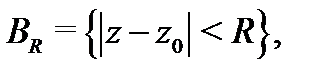 лежащем в области
лежащем в области 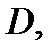 функция
функция 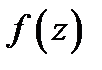 разлагается в степенной ряд
разлагается в степенной ряд
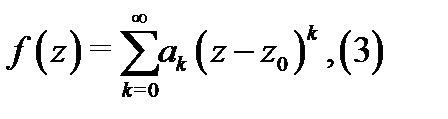
абсолютно сходящийся в круге 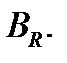 Этот ряд необходимо является рядом Тейлора
Этот ряд необходимо является рядом Тейлора 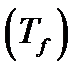
для функции 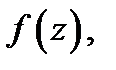 т.е.
т.е.
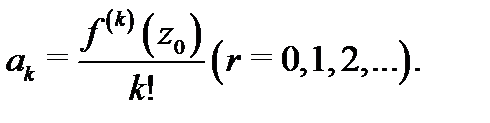
Таким образом, разложение аналитической функции в степенной ряд единственно.
 Доказательство. Возьмём произвольно точку
Доказательство. Возьмём произвольно точку  и опишем круг
и опишем круг 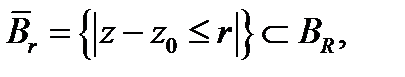 охватывающий точку
охватывающий точку 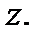 Так как функция
Так как функция 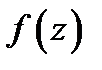 аналитична в односвязной области
аналитична в односвязной области 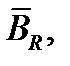 то для неё справедлива интегральная формула Коши:
то для неё справедлива интегральная формула Коши:
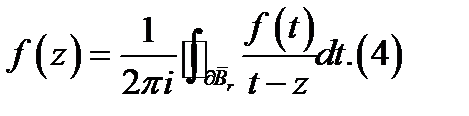
Преобразуем подынтегральное выражение следующим образом:
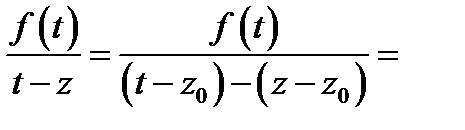
=[выносим за скобку вектор максимальной длины: 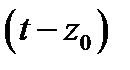 ]=
]=
= 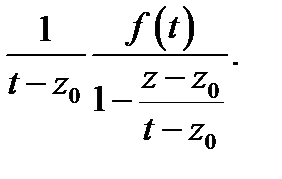 Так как
Так как
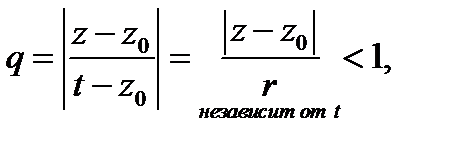
то геометрическая прогрессия
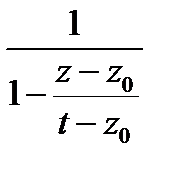 разлагается в равномерно сходящийся в круге
разлагается в равномерно сходящийся в круге 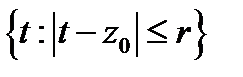 степенной ряд
степенной ряд
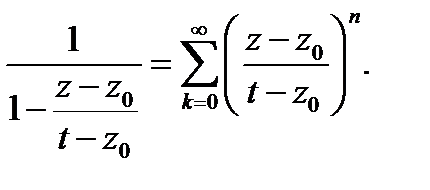
Поэтому
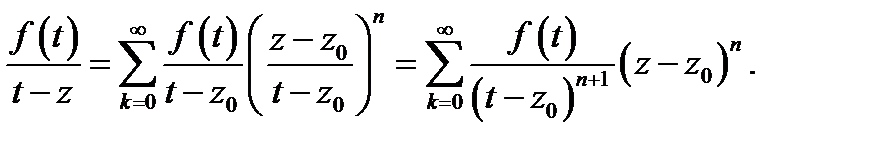
Подставляя это в (4), будем иметь
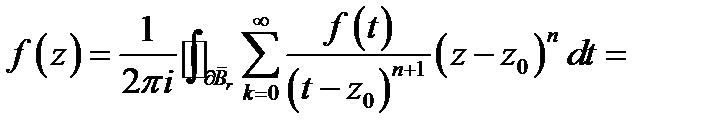
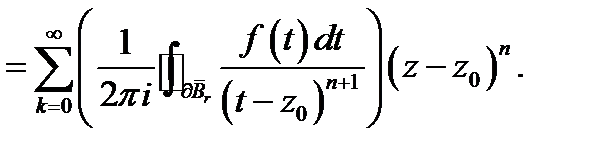
Учитывая, что
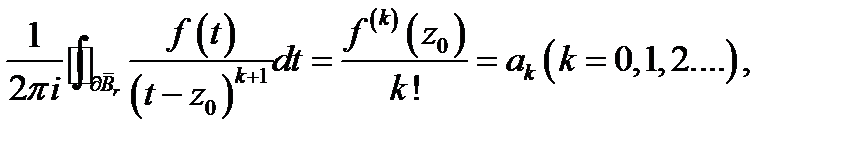
получаем утверждение нашей теоремы.
Для комплексных функций имеют место стандартные разложения в степенные ряды.
Таблица 1. Разложения основных элементарных функций в степенные ряды
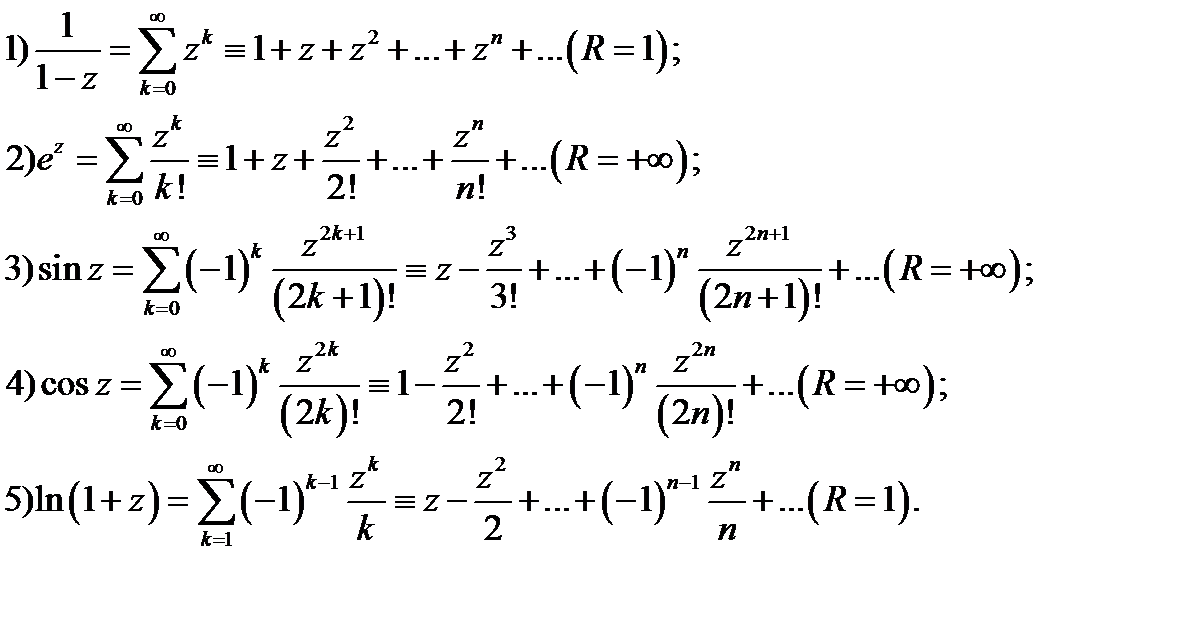
Дата добавления: 2016-06-05; просмотров: 4091;











