Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
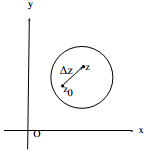 Так же, как и в действительном анализе, для функций комплексного переменного вводится понятие производной. Однако здесь это понятие более глубокое, чем в действительном анализе. Например, всякая линейная действительная функция дифференцируема в любой точке. Для комплексных функций это не так. Например, функция
Так же, как и в действительном анализе, для функций комплексного переменного вводится понятие производной. Однако здесь это понятие более глубокое, чем в действительном анализе. Например, всякая линейная действительная функция дифференцируема в любой точке. Для комплексных функций это не так. Например, функция 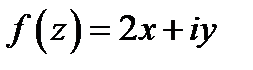 нигде не дифференцируема. Перейдём к изучению этого понятия.
нигде не дифференцируема. Перейдём к изучению этого понятия.
Пусть функция  определена в точке
определена в точке  и некоторой ее окрестности
и некоторой ее окрестности 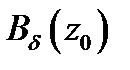 . Сместимся из точки
. Сместимся из точки 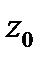 в точку
в точку 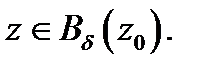 Тогда аргумент функции
Тогда аргумент функции 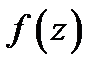 получит приращение
получит приращение 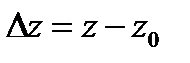 , а сама функция
, а сама функция 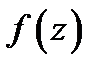 – приращение
– приращение 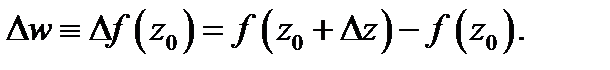
Определение 1. Если существует конечный предел
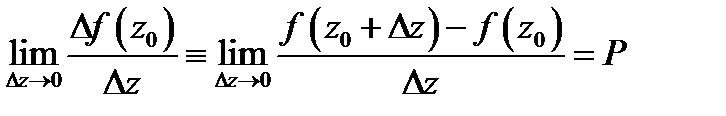
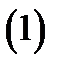
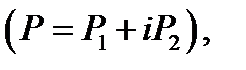
то его называют производной функции 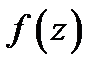 в точке
в точке 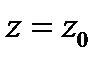 и обозначают
и обозначают 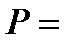
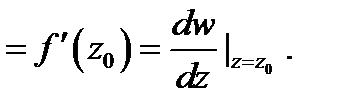
С понятием производной тесно связано понятие дифференцируемости функции в точке 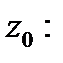 функция
функция 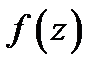 называется дифференцируемой в точке
называется дифференцируемой в точке 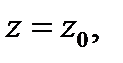 если её приращение в этой точке представляется в виде
если её приращение в этой точке представляется в виде
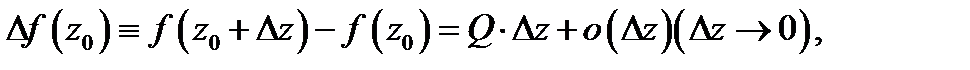
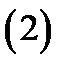
где 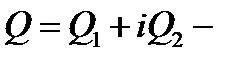 постоянная, не зависящая от
постоянная, не зависящая от 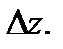 При этом величина
При этом величина 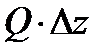 называется дифференциалом функции
называется дифференциалом функции 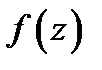 в точке
в точке 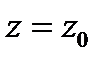 и обозначается
и обозначается 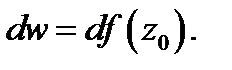 Разделив обе части равенства (2) на
Разделив обе части равенства (2) на 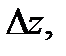 будем иметь
будем иметь 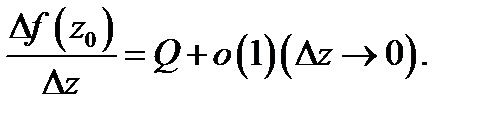 Последнее равенство означает, что существует предел (1), т.е. что существует производная
Последнее равенство означает, что существует предел (1), т.е. что существует производная 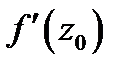 и что она равна
и что она равна 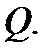 Таким образом, дифференцируемость функции
Таким образом, дифференцируемость функции 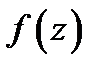 в точке
в точке 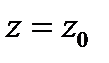 эквивалентна существованию производной
эквивалентна существованию производной 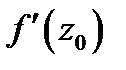 . При этом
. При этом 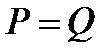 и значит,
и значит,
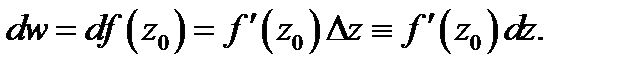
Как уже отмечалось выше, не любая (даже очень простая) функция дифференцируема в точке 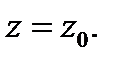 Для этого её мнимая и действительные части должны быть определенным образом подчинены друг другу в следующем смысле.
Для этого её мнимая и действительные части должны быть определенным образом подчинены друг другу в следующем смысле.
Теорема Коши-Римана. Для того чтобы функция 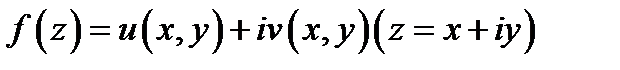 была дифференцируема в точке
была дифференцируема в точке 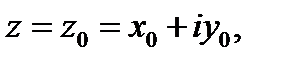 необходимо и достаточно, чтобы в точке
необходимо и достаточно, чтобы в точке 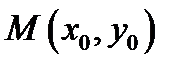 её действительная и мнимая части были дифференцируемы (как функции действительных переменных) и чтобы в этой точке имели место равенства
её действительная и мнимая части были дифференцируемы (как функции действительных переменных) и чтобы в этой точке имели место равенства
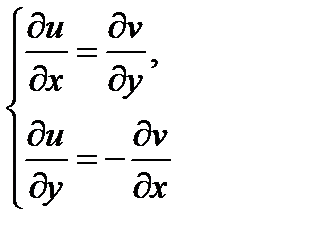
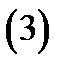
(равенства (3) называются условиями Коши-Римана).
Доказательство. Пусть функция 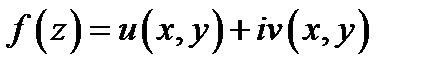 дифференцируема в точке
дифференцируема в точке 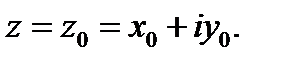 Тогда имеет место асимптотическое разложение (2). Запишем его более подробно:
Тогда имеет место асимптотическое разложение (2). Запишем его более подробно:
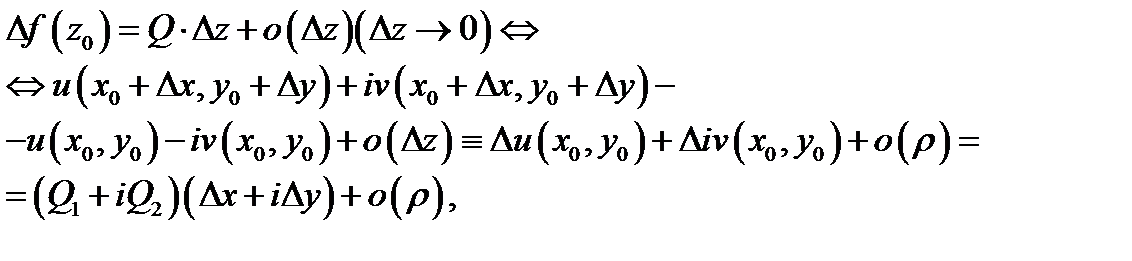
где 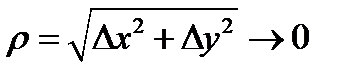 (очевидно, что
(очевидно, что 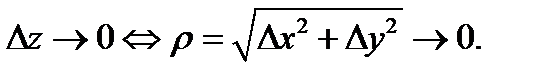 ) Отделяя здесь мнимые и действительные части, получим
) Отделяя здесь мнимые и действительные части, получим
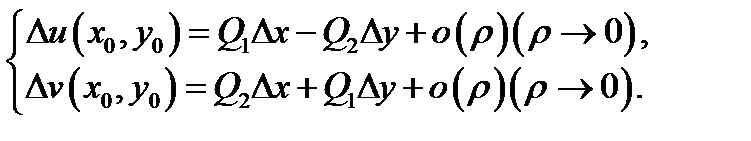
Эти равенства означают, во-первых, что функции 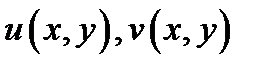 дифференцируемы как функции действительных переменных
дифференцируемы как функции действительных переменных 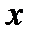 и
и  в точке
в точке 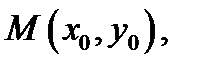 и, во-вторых,что имеют место равенства
и, во-вторых,что имеют место равенства
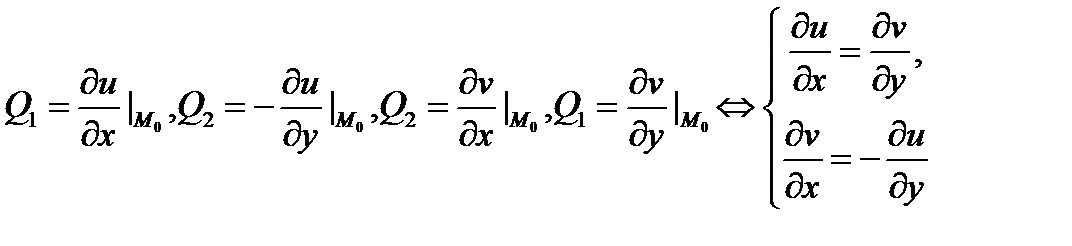 в точке
в точке 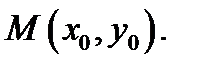
Таким образом, если функция 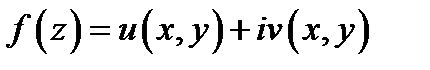 дифференцируема в точке
дифференцируема в точке 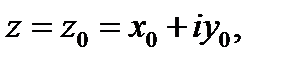 то имеют место условия Коши-Римана (3). Рассуждая обратным ходом, покажем, что при выполнении условий (3) функция
то имеют место условия Коши-Римана (3). Рассуждая обратным ходом, покажем, что при выполнении условий (3) функция 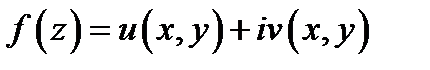 будет дифференцируемой в точке
будет дифференцируемой в точке 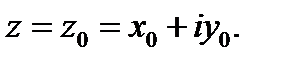 Теорема доказана.
Теорема доказана.
Замечание 1. Из доказательства теоремы следует, что если 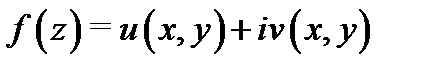 дифференцируема в точке
дифференцируема в точке 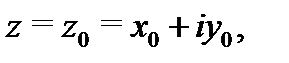 то ее производную в этой точке можно вычислять по формуле
то ее производную в этой точке можно вычислять по формуле 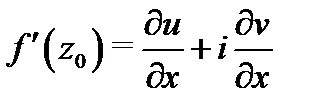 или по формуле
или по формуле 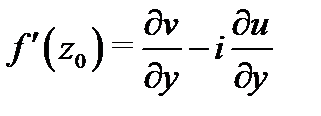 .
.
Пример 1.Проверить, будет ли функция 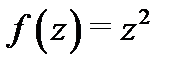 дифференцируемой. Если да, то найти её производную.
дифференцируемой. Если да, то найти её производную.
Решение.Выделим сначала в 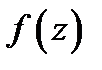 мнимую и действительные части:
мнимую и действительные части:
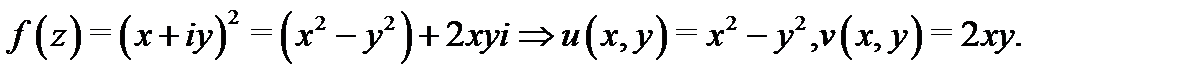
Теперь проверим условия Коши-Римана. Имеем
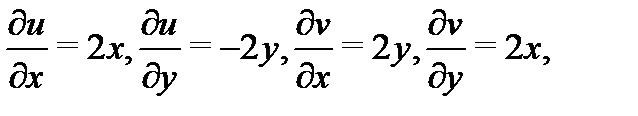
значит, условия (3) Коши-Римана выполняются для всех 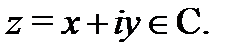 Следовательно, функция
Следовательно, функция 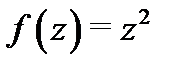 дифференцируема в любой точке
дифференцируема в любой точке 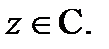 Её производную находим по формуле
Её производную находим по формуле
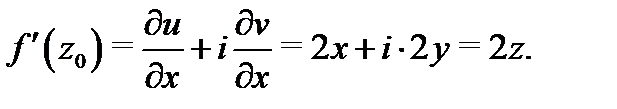
Таким образом, как и ожидалось, мы получили, что 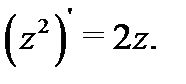 Забегая вперёд, отметим, что производные всех элементарных однозначных комплексных функций находятся по тем же правилам, что и производные действительных функций. Например,
Забегая вперёд, отметим, что производные всех элементарных однозначных комплексных функций находятся по тем же правилам, что и производные действительных функций. Например,
То же замечание справедливо и для отдельных ветвей многозначных функций. Например,
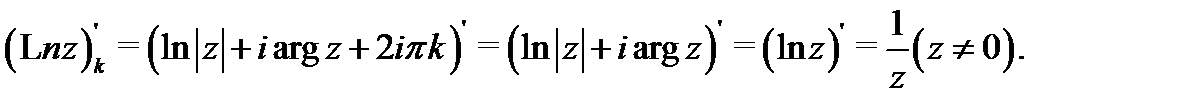
Введём теперь следующее важное понятие.
Определение 2.Функция  называется аналитической в точке
называется аналитической в точке 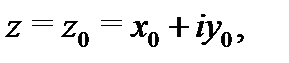 если она дифференцируема как в точке
если она дифференцируема как в точке 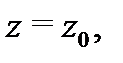 так и в некоторой её окрестности.
так и в некоторой её окрестности.
Аналитичность функции 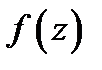 в точке
в точке 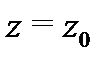 равносильна тому, что
равносильна тому, что 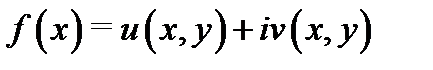 удовлетворяет условиям Коши-Римана (3) в некоторой окрестности точки
удовлетворяет условиям Коши-Римана (3) в некоторой окрестности точки 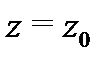 (включая и саму точку
(включая и саму точку 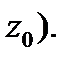
Определение 3.Функция 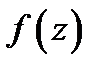 называется аналитической (регулярной, голоморфной) в области
называется аналитической (регулярной, голоморфной) в области 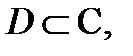 если она аналитична в любой точке этой области.
если она аналитична в любой точке этой области.
Заметим, что действительная и мнимая части аналитической функции удовлетворяют уравнению Лапласа: 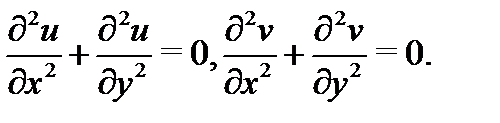 Это непосредственно вытекает из условий Коши-Римана. Функции, удовлетворяющие уравнению Лапласа, называются гармоническими.
Это непосредственно вытекает из условий Коши-Римана. Функции, удовлетворяющие уравнению Лапласа, называются гармоническими.
Пример 2.Является ли функция 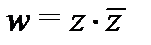 аналитической хотя бы в одной точке?
аналитической хотя бы в одной точке?
Решение.Так как 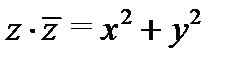 , то
, то 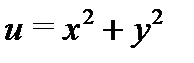 ,
, 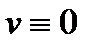 . Условия Коши–Римана имеют вид:
. Условия Коши–Римана имеют вид: 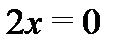 ,
, 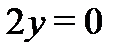 и выполняются только в точке
и выполняются только в точке 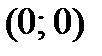 . Следовательно, функция
. Следовательно, функция 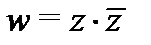 дифференцируема только в точке
дифференцируема только в точке 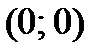 и нигде не аналитична. По определению (44) запишем:
и нигде не аналитична. По определению (44) запишем: 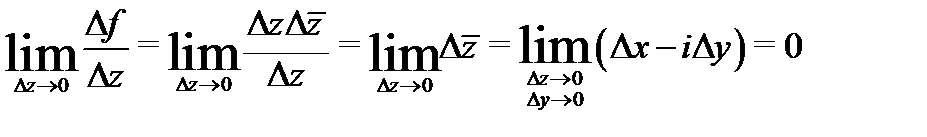 . Таким образом, производная
. Таким образом, производная 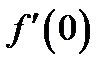 существует и равна нулю.
существует и равна нулю.
Так как мнимая и действительная части аналитической функции 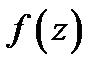 связаны условиями Коши-Римана (3), то
связаны условиями Коши-Римана (3), то 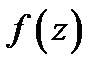 определяется (с точностью до постоянного слагаемого) либо своей действительной, либо мнимой частью. Покажем это на примере.
определяется (с точностью до постоянного слагаемого) либо своей действительной, либо мнимой частью. Покажем это на примере.
Пример 3.Найти аналитическую функцию, если известна ее мнимая часть 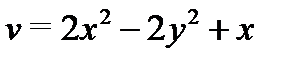 при дополнительном условии
при дополнительном условии 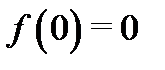 .
.
Решение.Так как 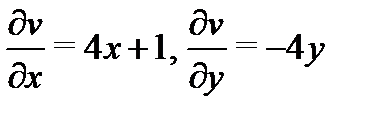 , то из условий Коши-Римана (3) находим производные действительной части:
, то из условий Коши-Римана (3) находим производные действительной части:
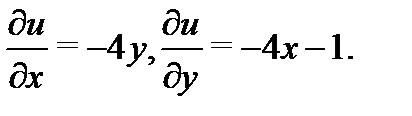
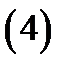
Решив первое из этих уравнений, находим 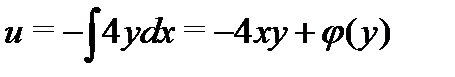 , где
, где 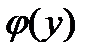 – произвольная функция переменной
– произвольная функция переменной 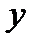 . Для определения
. Для определения 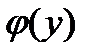 дифференцируем
дифференцируем 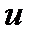 по
по 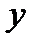 и подставляем в (2):
и подставляем в (2): 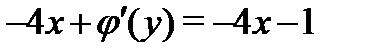 , откуда
, откуда 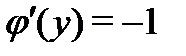 и
и 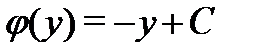 . Следовательно,
. Следовательно, 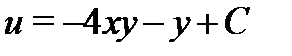 и окончательно получим:
и окончательно получим:
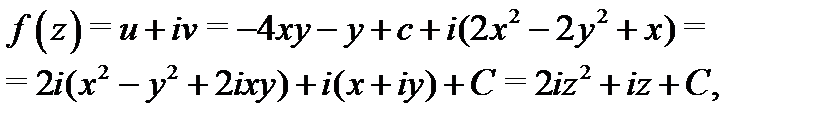
т.е. действительная часть восстанавливается с точностью до постоянного слагаемого. Условие 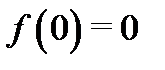 позволяет найти эту постоянную однозначно:
позволяет найти эту постоянную однозначно: 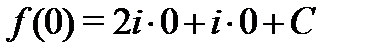
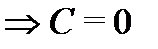 . Таким образом,
. Таким образом, 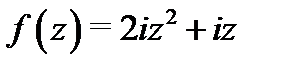 .
.
Имеют место следующие утверждения.
1. Степенная функция с натуральным показателем 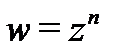 аналитична во всей комплексной плоскости
аналитична во всей комплексной плоскости 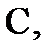 причем
причем 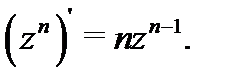
2. Каждая ветвь 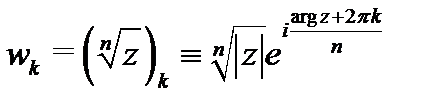
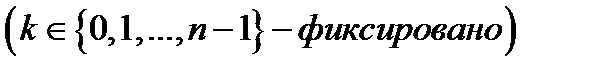 функции
функции 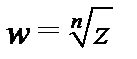 аналитична в области
аналитична в области 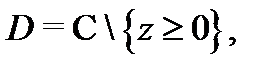 причем
причем 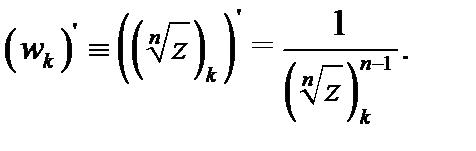
3. Комплексная экспонента 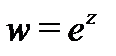 аналитична во всей плоскости
аналитична во всей плоскости  причем
причем 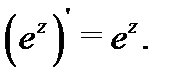
4. Комплексные тригонометрические функции 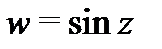 и
и 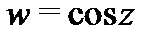 аналитичны во всей плоскости
аналитичны во всей плоскости 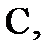 причем
причем 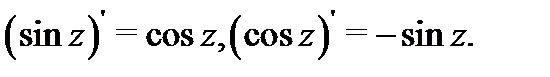 То же утверждение имеет место и для гиперболических функций, причем
То же утверждение имеет место и для гиперболических функций, причем 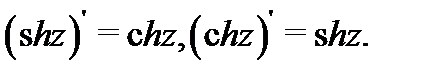
5. Каждая ветвь 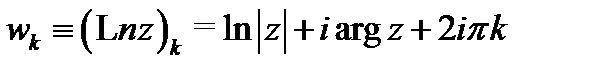
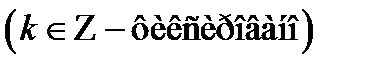 логарифмической функции аналитична в области
логарифмической функции аналитична в области 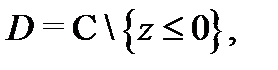 причем
причем
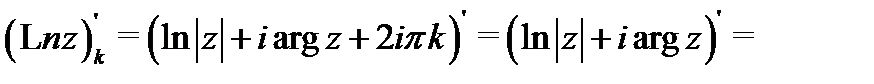
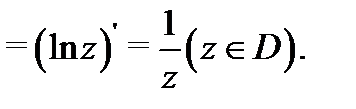
Все эти утверждения проверяются с помощью соотношений Коши-Римана.
2. Геометрический смысл модуля и аргумента производной
Пусть функция 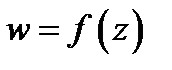 дифференцируема в точке
дифференцируема в точке 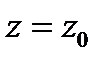 и
и 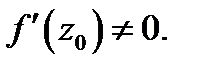 При отображении
При отображении 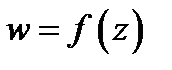 вектор
вектор 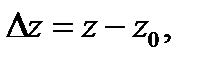 исходящий из точки
исходящий из точки 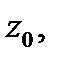 переходит в
переходит в
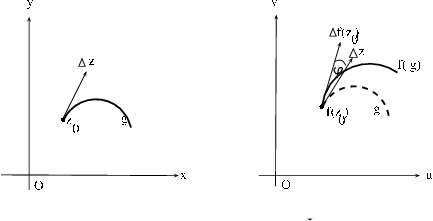
Рис. 8
бесконечно малый вектор 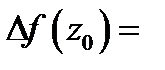
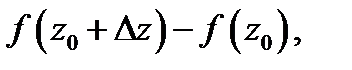 исходящий из точки
исходящий из точки 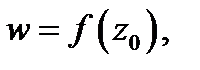 а гладкая кривая
а гладкая кривая  переходит в гладкую кривую
переходит в гладкую кривую  (см. рис. 8). Поскольку
(см. рис. 8). Поскольку 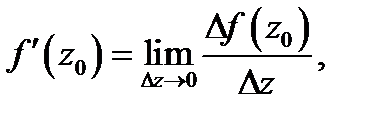 то выполняются одновременно следующие соотношения:
то выполняются одновременно следующие соотношения:
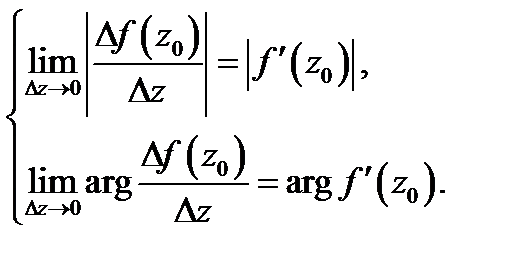
Отсюда следует, что с точностью до  выполняются равенства
выполняются равенства
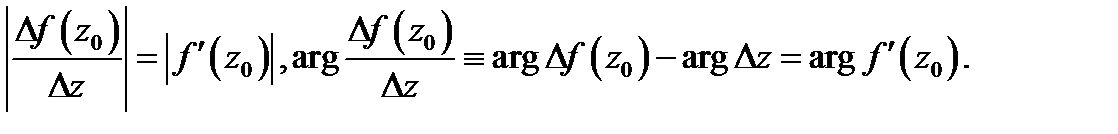
Эти равенства позволяют сделать следующие выводы (геометрический смысл модуля и аргумента производной ):
а) модуль 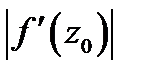 равен коэффициенту растяжения (сжатия) бесконечно малого вектора
равен коэффициенту растяжения (сжатия) бесконечно малого вектора 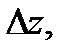 исходящего из точки
исходящего из точки 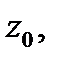 при отображении
при отображении 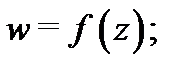
б) аргумент 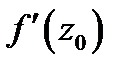 равен углу поворота
равен углу поворота 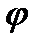 бесконечно малого вектора
бесконечно малого вектора 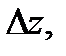 исходящего из точки
исходящего из точки 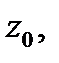 при отображении
при отображении 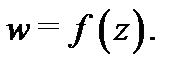
Эти утверждения верны для произвольного бесконечно малого вектора 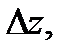 исходящего из точки
исходящего из точки 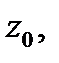 причем утверждение б) будет верно для любых гладких кривых
причем утверждение б) будет верно для любых гладких кривых 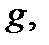 исходящих из точки
исходящих из точки 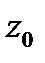 (в этом случае вектор
(в этом случае вектор 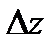 касается кривой
касается кривой 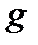 в точке
в точке 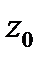 ). Если
). Если 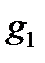 и
и 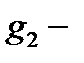 две гладкие кривые, исходящие из точки
две гладкие кривые, исходящие из точки 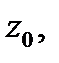 то из утверждения б) следует, что при отображении
то из утверждения б) следует, что при отображении 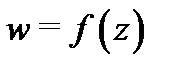 они развернутся на один и тот же угол, т.е. угол между кривыми
они развернутся на один и тот же угол, т.е. угол между кривыми 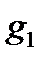 и
и 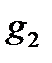 при отображении
при отображении 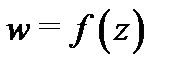 сохраняется. Более того, сохраняется и направление этого угла. Исходя из сказанного, вводят следующее понятие.
сохраняется. Более того, сохраняется и направление этого угла. Исходя из сказанного, вводят следующее понятие.
Определение 4. Отображение 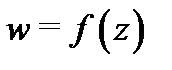 окрестности
окрестности 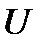 точки
точки 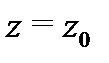 на окрестность
на окрестность 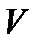 точки
точки 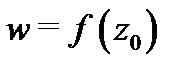 называется конформным, если оно обладает постоянством растяжения (сжатия) бесконечно малых элементов
называется конформным, если оно обладает постоянством растяжения (сжатия) бесконечно малых элементов 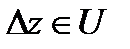 и сохранением углов и их направлением между любыми двумя гладкими кривыми
и сохранением углов и их направлением между любыми двумя гладкими кривыми 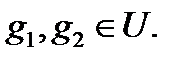 Отображение
Отображение 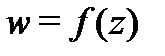 называется конформным в области
называется конформным в области 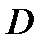 , если оно конформно в каждой точке области
, если оно конформно в каждой точке области 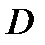 и если функция
и если функция 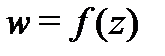 является аналитической и однолистной в области
является аналитической и однолистной в области 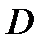 .
.
Теорема 2. Пусть функция 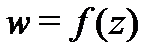 – однолистная и аналитическая в области
– однолистная и аналитическая в области 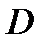 и
и 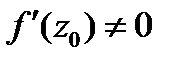 в каждой точке области
в каждой точке области 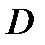 . Тогда отображение
. Тогда отображение 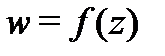 будет конформным в области
будет конформным в области 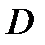 .
.
Доказательство этого утверждения вытекает из геометрического смысла производной и ее аргумента. Например, главная ветвь логарифма 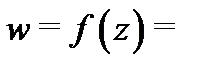
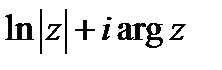 является конформным отображением области
является конформным отображением области 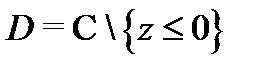 на область
на область 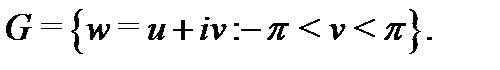 Конформные отображения играют важную роль в прикладных науках. Однако подробное их изучение в нашем курсе не позволяет дефицит времени. Читателю, заинтересованному в более детальном ознакомлении с теорией конформных отображений, рекомендуем книгу Б.А. Фукса и Б.В. Шабата ``Функции комплексного переменного и некоторые их приложения'' (ГИФМЛ, Москва, 1959) .
Конформные отображения играют важную роль в прикладных науках. Однако подробное их изучение в нашем курсе не позволяет дефицит времени. Читателю, заинтересованному в более детальном ознакомлении с теорией конформных отображений, рекомендуем книгу Б.А. Фукса и Б.В. Шабата ``Функции комплексного переменного и некоторые их приложения'' (ГИФМЛ, Москва, 1959) .
======================================================
Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
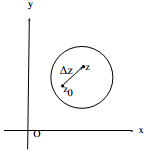 Везде ниже, если не оговорено противное, функция
Везде ниже, если не оговорено противное, функция 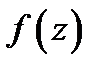 предполагается однозначной в своей области определения. Пусть в плоскости
предполагается однозначной в своей области определения. Пусть в плоскости 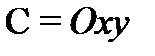 задана некоторая ориентированная кривая
задана некоторая ориентированная кривая 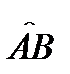 (
( 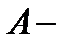 начало,
начало, 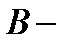 конец). Каждой точке
конец). Каждой точке 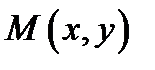 плоскости
плоскости 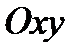 соответствует единственное комплексное число
соответствует единственное комплексное число 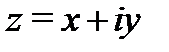 (и обратно), поэтому будем отождествлять точку
(и обратно), поэтому будем отождествлять точку  и соответствующее комплексное число
и соответствующее комплексное число  и будем писать
и будем писать 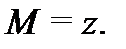 Пусть функция
Пусть функция 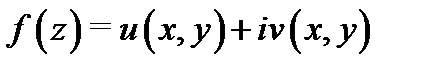 определена на кривой
определена на кривой  . Разобъём кривую
. Разобъём кривую  на частичные дуги
на частичные дуги 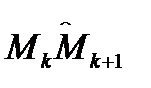 точками
точками 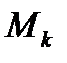 в направлении ориентации кривой:
в направлении ориентации кривой:
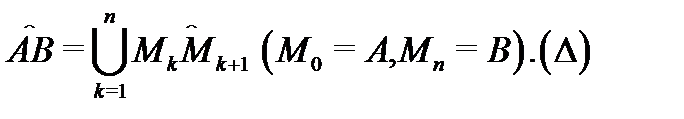
Возьмём произвольно точку  и составим интегральную сумму
и составим интегральную сумму 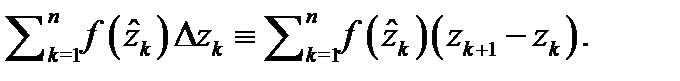 Обозначим
Обозначим 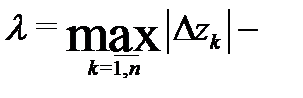 диаметр разбиения
диаметр разбиения 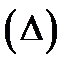 .
.
Определение 5.Если существует конечный предел интегральных сумм:
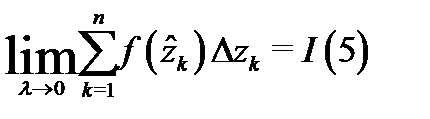
и он не зависит от вида разбиения  и выбора точек
и выбора точек 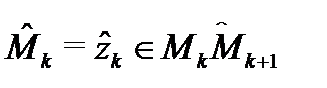 , то его называют интегралом от функции
, то его называют интегралом от функции 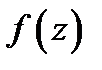 вдоль кривой (дуги)
вдоль кривой (дуги)  и обозначают
и обозначают 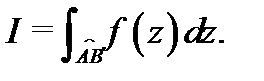 При этом функцию
При этом функцию 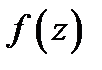 называется интегрируемой на кривой
называется интегрируемой на кривой 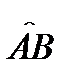 .
.
Сразу же отметим свойство ориентированности этого интеграла:
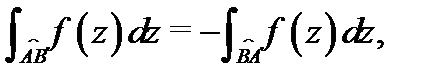
которое вытекает из того, что при ориентации кривой от 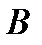 до
до 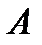 вектор
вектор 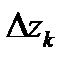 заменяется на вектор
заменяется на вектор 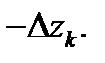 Кроме того, интеграл от комплексной функции, очевидно, обладает свойствами линейности и аддитивности, которые мы не выписываем. Следующее утверждение позволяет свести комплексный интеграл к двум действительным криволинейным интегралам.
Кроме того, интеграл от комплексной функции, очевидно, обладает свойствами линейности и аддитивности, которые мы не выписываем. Следующее утверждение позволяет свести комплексный интеграл к двум действительным криволинейным интегралам.
Теорема 3. Пусть ограниченная дуга 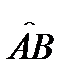 кусочно-гладка и лежит в области
кусочно-гладка и лежит в области 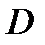 определения функии
определения функии 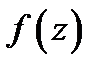 . Пусть, кроме того,
. Пусть, кроме того, 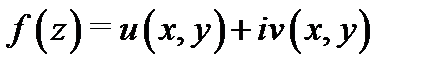 непрерывна на дуге
непрерывна на дуге 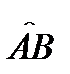 . Тогда имеет место равенство
. Тогда имеет место равенство
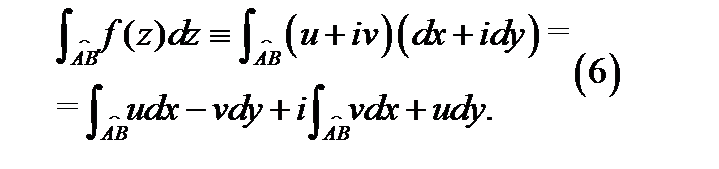
Доказательство. Преобразуем в интегральной сумме (5) слагаемое 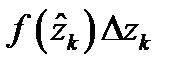 :
:
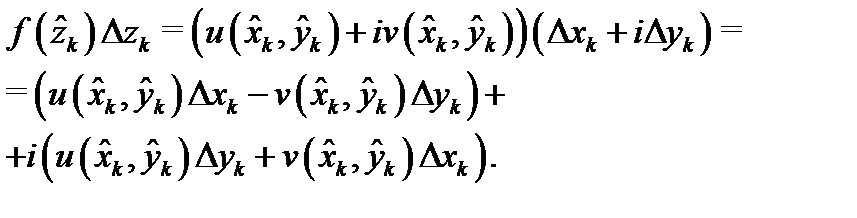
Тогда интегральная сумма в равенсте (5) примет вид
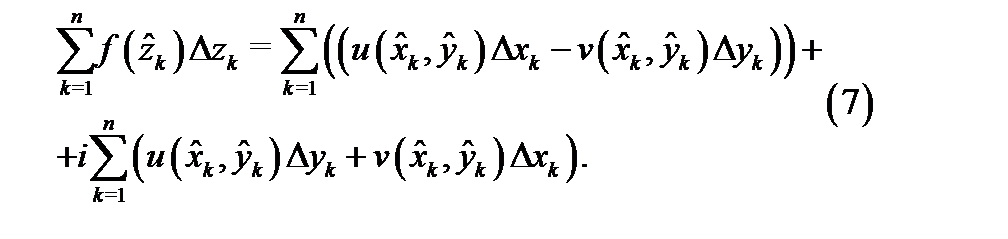
Здесь действительная часть является интегральной суммой для криволинейного интеграла 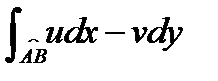 , а мнимая часть – интегральной суммой для криволинейного интеграла
, а мнимая часть – интегральной суммой для криволинейного интеграла 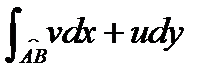 . Так как функция
. Так как функция  непрерывна на дуге
непрерывна на дуге  то на этой дуге непрерывны ее действительная часть
то на этой дуге непрерывны ее действительная часть 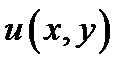 и мнимая часть
и мнимая часть 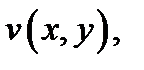 поэтому указанные криволинейные действительные интегралы существуют. Переходя к пределу в равенстве (7) при
поэтому указанные криволинейные действительные интегралы существуют. Переходя к пределу в равенстве (7) при 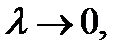 получаем равенство (6). Теорема доказана.
получаем равенство (6). Теорема доказана.
Из этой теоремы вытекают свойства линейности, аддитивности и другие свойства комплексного интеграла. В частности, справедлива теорема об оценке интеграла.
Теорема 4.Если функция 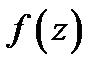 непрерывна на кусочно-гладкой ограниченной кривой
непрерывна на кусочно-гладкой ограниченной кривой 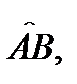 то имеет место неравенство
то имеет место неравенство
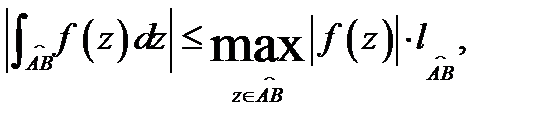
где 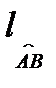 – длина дуги.
– длина дуги.
Из теоремы 3 вытекает также следующее утверждение.
Теорема 5.Пусть дуга 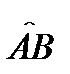 задана параметрически уравнением
задана параметрически уравнением
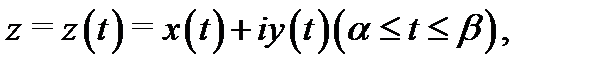
причем функция 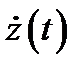 непрерывна на отрезке
непрерывна на отрезке 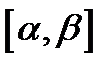 и дуга
и дуга 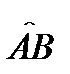 ориентирована по возрастанию параметра
ориентирована по возрастанию параметра 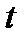 (т.е.
(т.е. 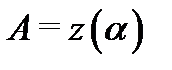 – начало,
– начало, 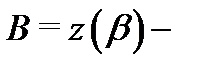 конец дуги
конец дуги  ). Пусть, кроме того, функция
). Пусть, кроме того, функция 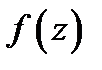 непрерывна на дуге
непрерывна на дуге 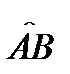 .Тогда имеет место равенство
.Тогда имеет место равенство
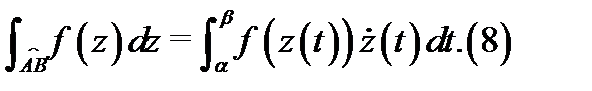
В качестве примера вычислим имеющий широкое применение в дальнейшей теории интеграл 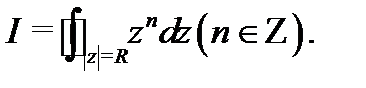 Покажем, что
Покажем, что
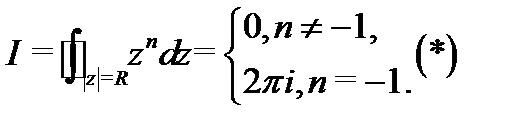
Имеем 
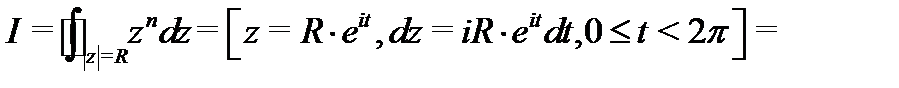
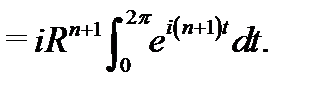
Если 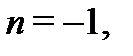 то
то 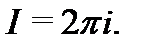 Если
Если 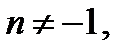 то
то
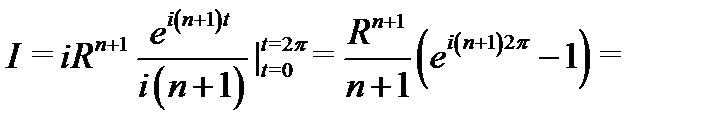
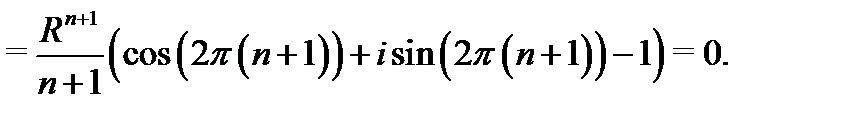
Равенство 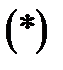 доказано.
доказано.
2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
Напомним, что множество
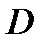 называется односвязным, если любой замкнутый контур, лежащий в
называется односвязным, если любой замкнутый контур, лежащий в 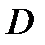 можно стянуть в точку, не выходя из
можно стянуть в точку, не выходя из 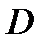 . Множество
. Множество 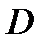 называется
называется 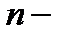 связным, если его граница
связным, если его граница 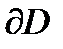 состоит из
состоит из 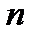 попарно не пересекающихся между собой замкнутых контуров.
попарно не пересекающихся между собой замкнутых контуров.
Например, на рисунке A изображена односвязная область, на рисунке B – 4-связная область (одна внешняя граница и три внутренних границ). При этом будем говорить, что направление на границе 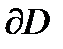 является положительным (
является положительным ( 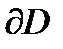 – положительно ориентирована), если при её обходе область
– положительно ориентирована), если при её обходе область 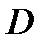 остаётся слева. Например, на рисунке C граница двухсвязной области положительно ориентирована. Ориентация, противоположная положительной, называется отрицательной.
остаётся слева. Например, на рисунке C граница двухсвязной области положительно ориентирована. Ориентация, противоположная положительной, называется отрицательной.
Теорема Коши для односвязной области.Пусть область 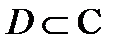 односвязная и функция
односвязная и функция 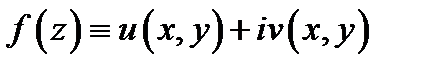 аналитична в
аналитична в  Тогда каков бы ни был кусочно-гладкий замкнутый контур
Тогда каков бы ни был кусочно-гладкий замкнутый контур  лежащий внутри
лежащий внутри  интеграл от
интеграл от 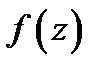 по
по 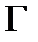 равен нулю.
равен нулю.
Доказательство.Вычислим интеграл
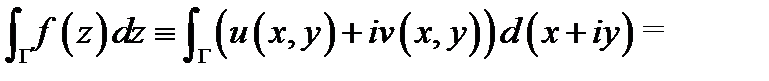
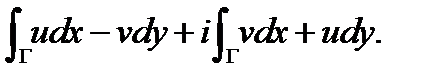
Воспользуемся формулой Грина:
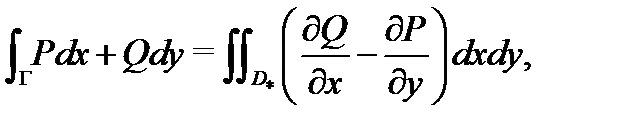
где  область, охватываемая контуром
область, охватываемая контуром  Будем иметь
Будем иметь
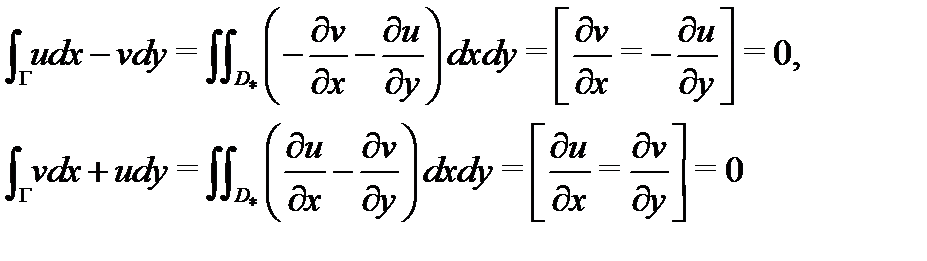
(здесь в квадратных скобках выписаны условия Коши-Римана, которые выполняются, так как функция 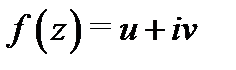 аналитична в области
аналитична в области 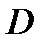 ). Теорема доказана.
). Теорема доказана.
Теорема Коши для многосвязной области.Пусть область 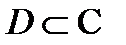
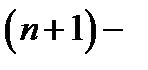 связна,причем
связна,причем 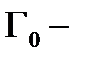 её внешняя граница, а
её внешняя граница, а 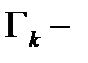 её внутренние границы, обходимые все против часовой стрелки. Пусть функция
её внутренние границы, обходимые все против часовой стрелки. Пусть функция 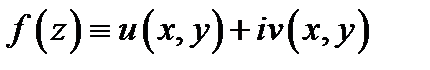 аналитична в
аналитична в  Тогда имеет место равенство
Тогда имеет место равенство

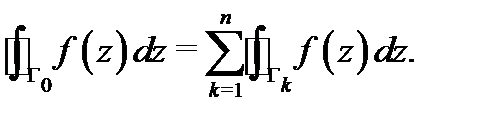
Доказательствопроведём для двухсвязной области 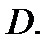 Сделаем разрез
Сделаем разрез 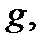 соединяющий внутреннюю и внешнюю границы
соединяющий внутреннюю и внешнюю границы 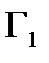 и
и 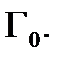 Тогда область
Тогда область 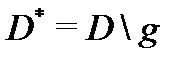 будет односвязной, а замкнутый контур
будет односвязной, а замкнутый контур 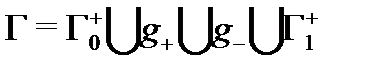 лежит в
лежит в 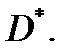 Значит, для этого контура справедлива предыдущая теорема:
Значит, для этого контура справедлива предыдущая теорема: 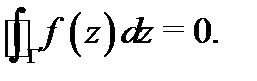 Применяя свойство аддитивности интеграла, будем иметь
Применяя свойство аддитивности интеграла, будем иметь
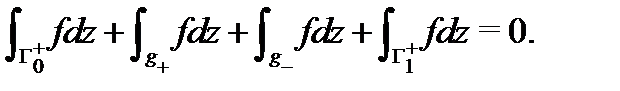
Рис. 10 Учитывая, что 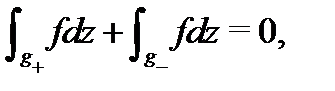 приходим к равенству
приходим к равенству
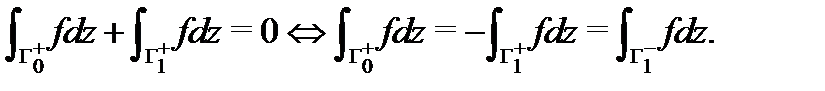
Остаётся учесть что здесь контуры 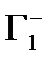 и
и 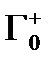 обходятся против часовой стрелки. Теорема доказана.
обходятся против часовой стрелки. Теорема доказана.
И, наконец, сформулируем без доказательство следующее важное утверждение.
Интегральная теорема Коши. Пусть функция 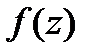 аналитична в односвязной области
аналитична в односвязной области 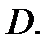 Тогда какова бы ни была точка
Тогда какова бы ни была точка 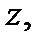 лежащая внутри области
лежащая внутри области 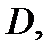 и замкнутый кусочно-гладкий контур
и замкнутый кусочно-гладкий контур 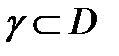 , охватывающий точку
, охватывающий точку 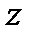 и обходимый против часовой стрелки, справедлива интегральная формула Коши
и обходимый против часовой стрелки, справедлива интегральная формула Коши
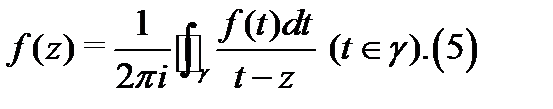
При этом функция 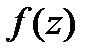 имеет всюду в
имеет всюду в 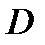 производные любого порядка, для которых справедлива формула
производные любого порядка, для которых справедлива формула
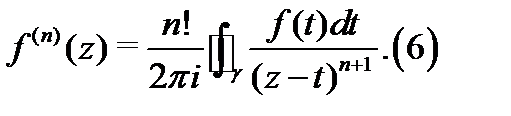
Замечание. Если функция аналитична в замкнутой ограниченной области 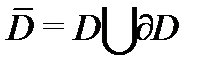 с кусочно гладкой границей
с кусочно гладкой границей 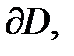 то в качестве контура
то в качестве контура 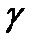 в (6) можно взять границу
в (6) можно взять границу 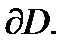 Тогда из (5) вытекает, что аналитическая в
Тогда из (5) вытекает, что аналитическая в 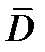 функция
функция 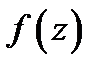 полностью определяется своими значениями на границе
полностью определяется своими значениями на границе 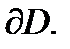 Таким свойством действительные функции не обладают.
Таким свойством действительные функции не обладают.
Интегральная формула Коши имеет многочисленные применения, о которых будет сказано в дальнейшим. Рассмотрим несколько примеров[i].
Пример 1.Вычислить 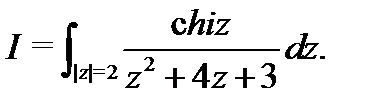
Решение. Внутри окружности 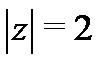 знаменатель дроби обращается в нуль в точке
знаменатель дроби обращается в нуль в точке 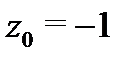 . Для удобства применения формулы (5) перепишем интеграл в виде
. Для удобства применения формулы (5) перепишем интеграл в виде
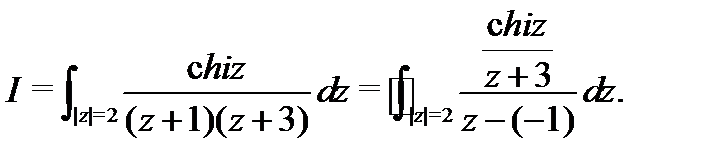
Здесь 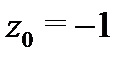 и
и 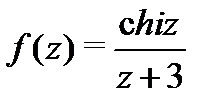 аналитична в круге
аналитична в круге 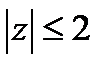 . Тогда
. Тогда 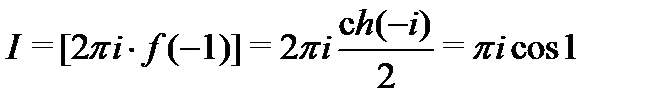 .
.
Пример 2.Вычислить 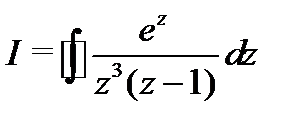 : по
: по
а) контуру 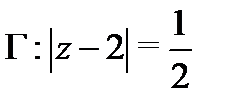 ; б)
; б) 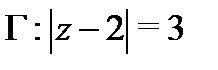 .
.
Решение.а) В круге 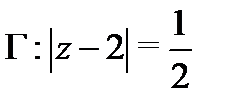 функция
функция 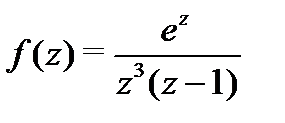 аналитична. Следовательно, по теореме Коши для односвязной области получаем, что
аналитична. Следовательно, по теореме Коши для односвязной области получаем, что 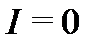 .
.
Рис. 11
б) Так как внутри контура интегрирования знаменатель подынтегральной функции обращается в нуль в точках 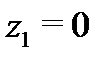 и
и 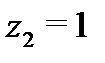 , то для того, чтобы стало возможным применить формулу (5), рассмотрим многосвязную область
, то для того, чтобы стало возможным применить формулу (5), рассмотрим многосвязную область 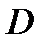 (рис. 11), ограниченную окружностью
(рис. 11), ограниченную окружностью 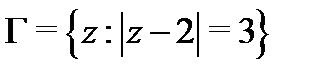 и внутренними контурами
и внутренними контурами 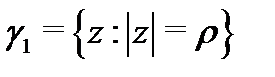 и
и 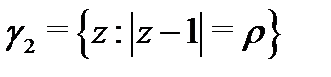
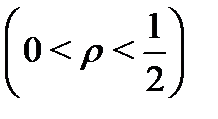 .
.
Тогда в области 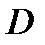 функция
функция 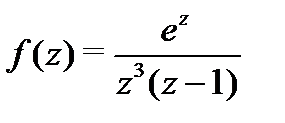 является аналитической, и по теореме Коши для многосвязной области можно записать:
является аналитической, и по теореме Коши для многосвязной области можно записать:
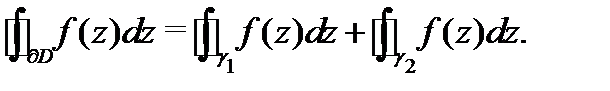
Для вычисления интегралов справа применим формулу (5):
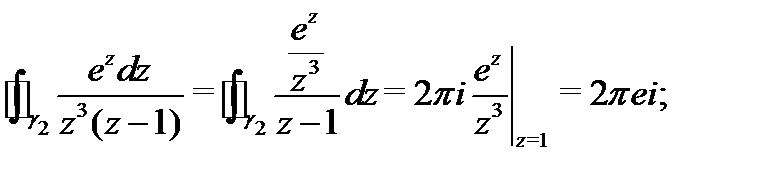
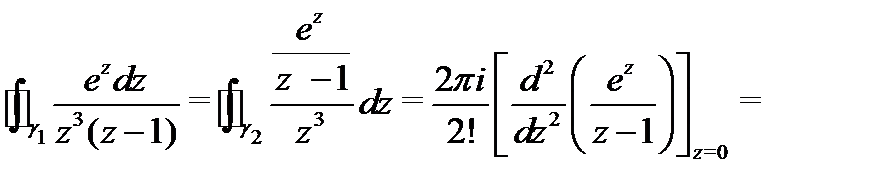
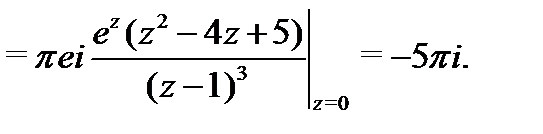
Таким образом, 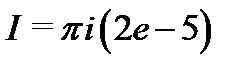 .
.
3. Первообразная функции комплексных переменных
Функция 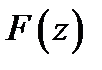 называется первообразной функции
называется первообразной функции 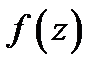 в области в области
в области в области 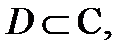 если
если 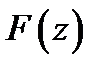 дифференцируема в
дифференцируема в 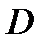 и
и 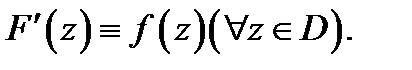
Из теоремы Коши для односвязной области следует, что интеграл 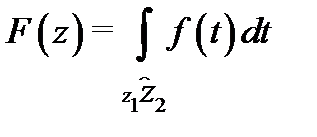 не зависит от формы пути
не зависит от формы пути 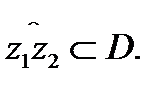 Поэтому можно сформулировать следующее утверждение.
Поэтому можно сформулировать следующее утверждение.
Теорема 1.Если однозначная функция 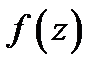 дифференцируема в односвязной области
дифференцируема в односвязной области 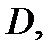 то она имеет первообразную в этой области. Одной из первообразных является интеграл
то она имеет первообразную в этой области. Одной из первообразных является интеграл 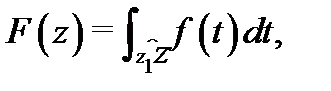 где
где 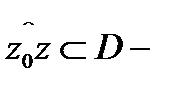 любой кусочно-гладкий путь, соединяющий фиксированную точку
любой кусочно-гладкий путь, соединяющий фиксированную точку 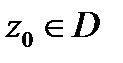 с текущей точкой
с текущей точкой 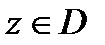 . Все остальные первообразные имеют вид
. Все остальные первообразные имеют вид 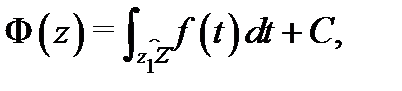 где
где 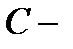 произвольная комплексная постоянная.
произвольная комплексная постоянная.
Доказательство этой теоремы проводится так же, как и в действительном анализе. Используя эту теорему, нетрудно доказать следующие утверждения.
1. Если функция 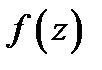 аналитична в односвязной области
аналитична в односвязной области 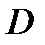 и
и 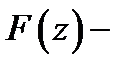 её первообразная в
её первообразная в 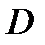 , то справедлива формула Ньютона-Лейбница
, то справедлива формула Ньютона-Лейбница
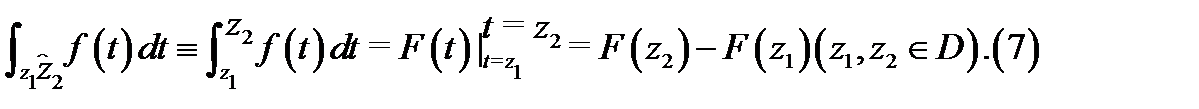
2. Если функция 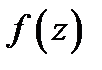 аналитична в односвязной области
аналитична в односвязной области 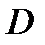 и
и 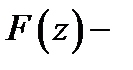 её первообразная в
её первообразная в 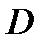 , то справедлива формула интегрирования по частям
, то справедлива формула интегрирования по частям
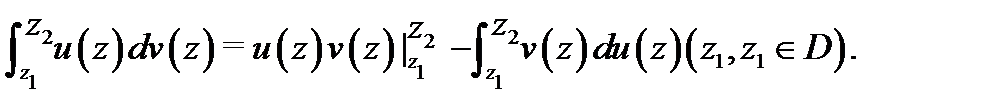
Замена переменных в интегралах от функции комплексного переменного аналогична случаю функции действительного переменного. Пусть аналитическая функция 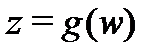 отображает взаимно однозначно кусочно-гладкий контур
отображает взаимно однозначно кусочно-гладкий контур 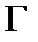 в плоскости
в плоскости 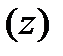 на контур
на контур 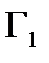 в плоскости
в плоскости 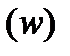 . Тогда
. Тогда
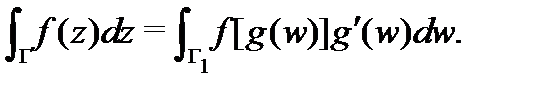
Замечание 2.Интегралы от элементарных однозначных функций в односвязных областях вычисляются по тем же формулам, что и в действительном анализе. Если же область  неодносвязна, то это правило может нарушаться. Для вычисления интеграла от многозначной функции указывается, какая именно однозначная ветвь ее берется (см. ниже пример 7). Это достигается заданием значения многозначной функции в некоторой точке контура интегрирования. Если контур интегрирования
неодносвязна, то это правило может нарушаться. Для вычисления интеграла от многозначной функции указывается, какая именно однозначная ветвь ее берется (см. ниже пример 7). Это достигается заданием значения многозначной функции в некоторой точке контура интегрирования. Если контур интегрирования  замкнут, то начальной точкой
замкнут, то начальной точкой 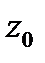 пути интегрирования считается та, в которой задано значение подынтегральной функции. Рассмотрим примеры.
пути интегрирования считается та, в которой задано значение подынтегральной функции. Рассмотрим примеры.
Пример 3.Вычислить 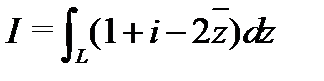 по кривой
по кривой 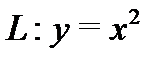 , соединяющей точки
, соединяющей точки 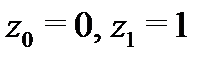 .
.
Решение. Для параболы 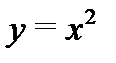 имеем
имеем 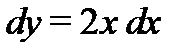 ,
, 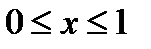 . По теореме 1 предыдущей лекции имеем
. По теореме 1 предыдущей лекции имеем
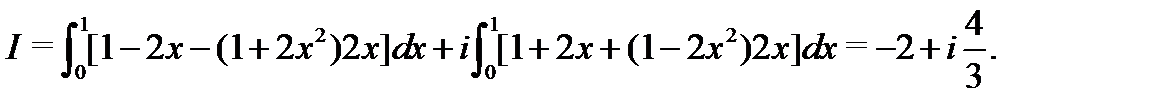
Пример 4.Вычислить 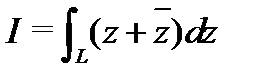 , где
, где 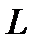 – дуга окружности
– дуга окружности 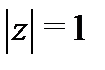 ,
, 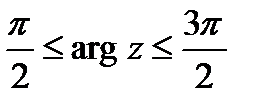 .
.
Решение. Положим 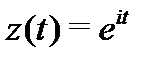 ,
, 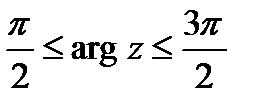 . Тогда
. Тогда 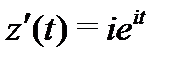 , и по формуле (49) находим:
, и по формуле (49) находим:
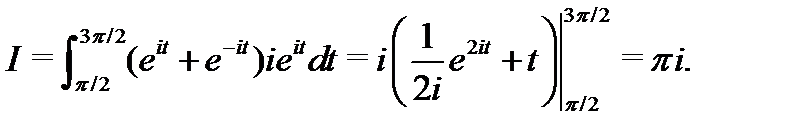
Пример 5.Вычислить 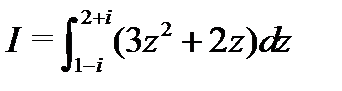 .
.
Решение. Так как подынтегральная функция 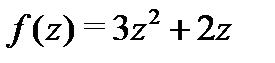 аналитична всюду, то по формуле (7) вычисляем:
аналитична всюду, то по формуле (7) вычисляем: 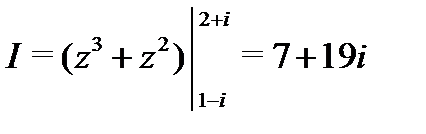 .
.
Пример 6. Вычислить 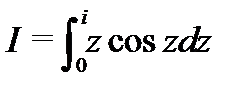 .
.
Решение. Функции 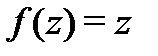 и
и 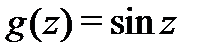 аналитичны всюду. По теореме 3 предыдущей лекции получаем, что
аналитичны всюду. По теореме 3 предыдущей лекции получаем, что
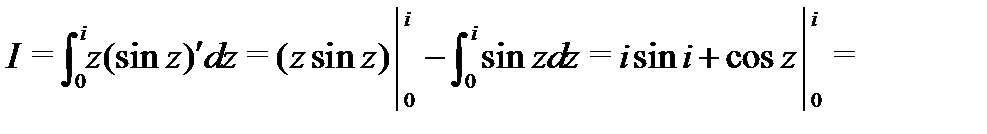
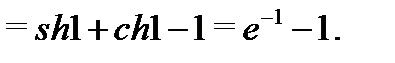
Пример 7. Вычислить 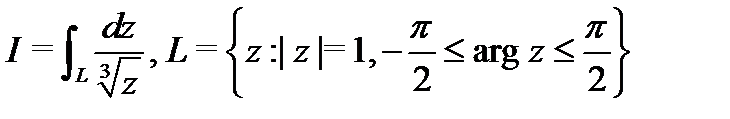 ,
, 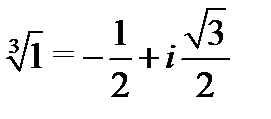 .
.
Решение. Функция 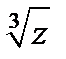 является многозначной:
является многозначной: 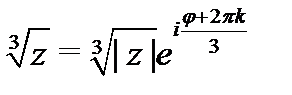 ,
, 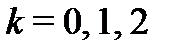 ;
;











