Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце

Сначала введём следующее понятие.

Определение 1. Ряд вида

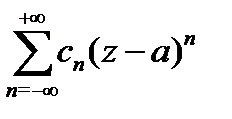
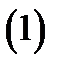
называетсядвухсторонним степенным рядом или рядом Лорана.

Ряд вида (1) сходится в области, в которой сходятся одновременно ряды

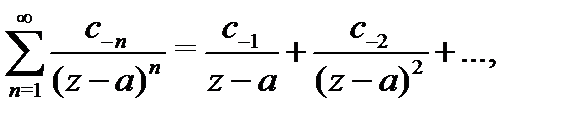
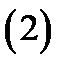
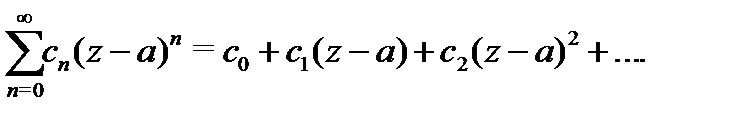
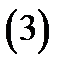
Ряд (2) сходится в области 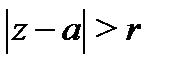, т.е. вне замкнутого круга с центром в точке 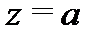и радиуса 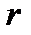, а ряд (3) – в круге 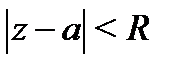. Поэтому: если 1) 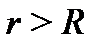, то ряд (1) расходится всюду; 2) если 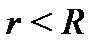, то ряд (1) сходится в кольце .

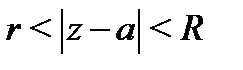Пример 1.Определить область сходимости ряда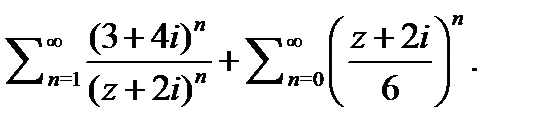

Решение. Для первого из рядов имеем 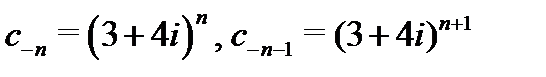, Следовательно, 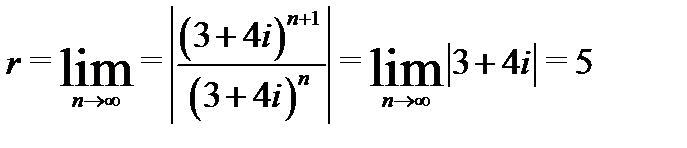. Значит, первый ряд сходится в области 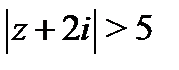. Для второго ряда имеем 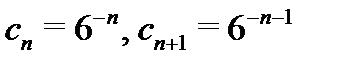. Радиус его сходимости 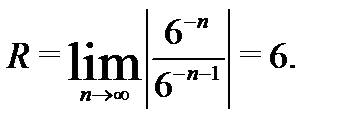Значит, второй ряд сходится в области 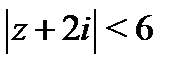. Таким образом, исходный двухсторонний ряд ряд сходится в кольце .

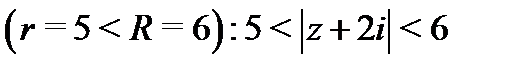На предыдущей лекции была доказана теорема 2, из которой следует, что если функция 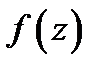аналитична в 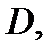то в окрестности любой точки 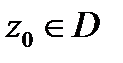она не может быть представлена в виде двухстороннего степенного ряда (1). Какие же функции представляются такими рядами? Ясно, что такие функции должны терять аналитичность в точке 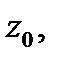т.е. эта точка должна быть особой для 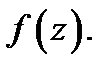Дадим более точное понятие особой точки.

Определение 2.Говорят, что точка 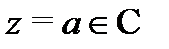является изолированной особой точкой для функции 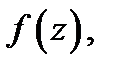если сушествует проколотая окрестность 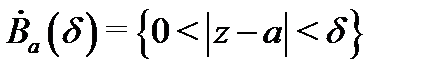этой точки такая, что функция 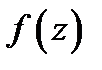аналитична в 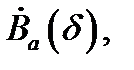но в самой точке 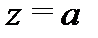она либо не определена, либо на аналитична.

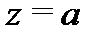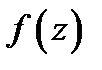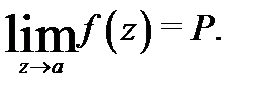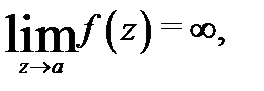Определение 3.Изолированная особая точка функции называется устранимой особой точкой, если существует конечный предел Если то точка 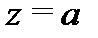называется полюсом. Полюс 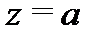называется полюсом 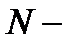го порядка, если существует конечный предел 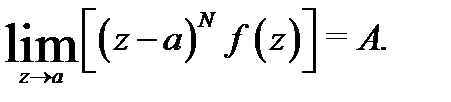И, наконец, точка 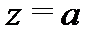называется существенно особой точкой для 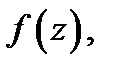если не существует ни конечный, ни бесконечный предел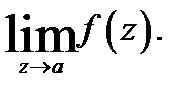

Нетрудно видеть, что если функция 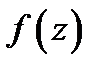аналитична в точке 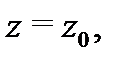то она разлагается в степенной ряд 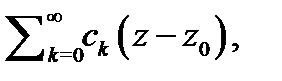абсолютно сходящийся в круге с центром в точке 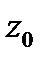и с радиусом, равным расстоянию от 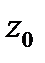до ближайшей особой точки 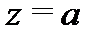функции .

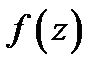1. Разложение функции в ряд Лорана

Следующее утверждение устанавливает условия разложимости функции в двусторонние степенные ряды.

Теорема Лорана.Если функция 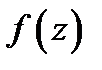аналитична в кольце

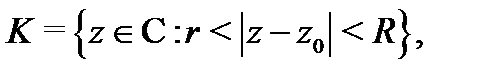
то в любой точке 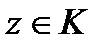этого кольца она разлагается в двухсторонний степенной ряд

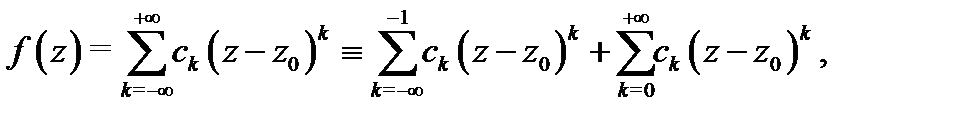
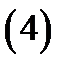
абсолютно сходящийся к 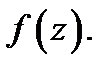При этом коэффициенты ряда (4) вычисляются по формулам

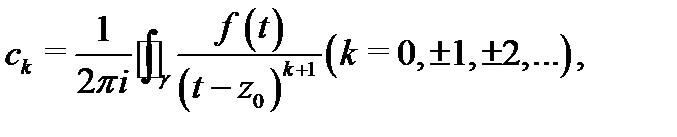
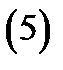
где 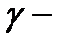любой кусочно-гладкий замкнутый контур, лежащий в кольце 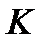, охватывающий точку 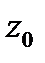и обходимый против часовой стрелки.

Доказательства этого утверждения основано на применении интегральной формулы Коши и проводится по аналогии с доказательством теоремы Тейлора.

Заметим, что ряд (4) называется рядом Лорана для функции 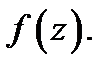При этом его часть 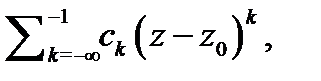состоящая из отрицательных степеней двучлена 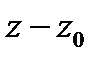называется главной частью, а часть 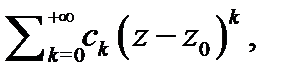состоящая из неотрицательных степеней двучлена 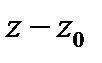– правильной частью ряда Лорана (4) . Чуть позже будет установлена связь типа изолированной особой точки функции 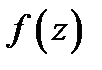c разложением в окрестности этой точки в ряд Лорана функции .

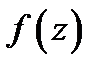Рассмотрим примеры[4].

Пример 2.Разложить функцию 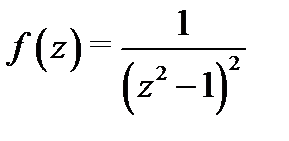в ряд Лорана в кольце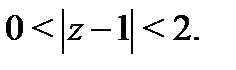

Решение.Надо представить функцию в виде ряда 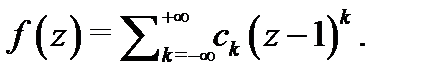Преобразуем данную функцию:

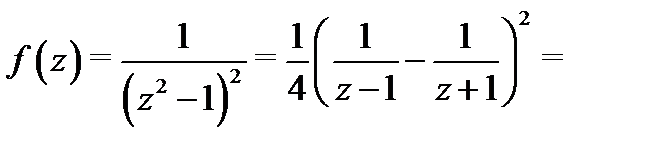
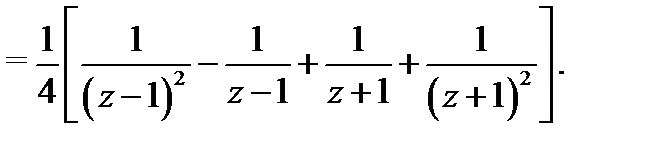
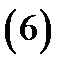
Первые два слагаемых в правой части (6) имеют нужный вид, так как представляют собой степени разности 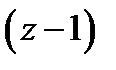. Последние два слагаемых запишем в виде:

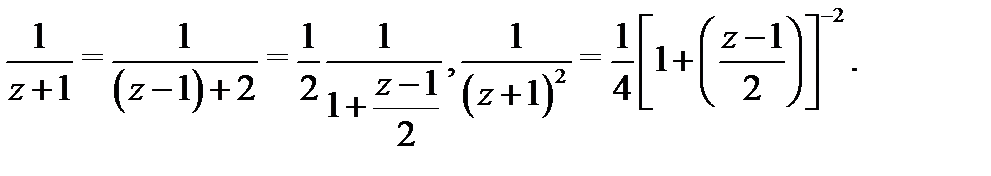
Применив формулу 1 таблицы 1, будем иметь

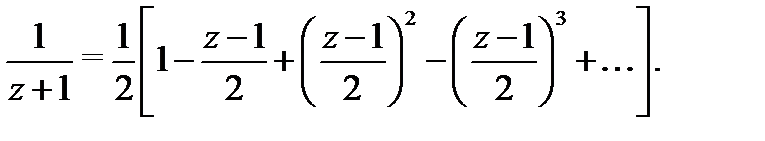
Дифференцированием по 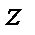находим, что

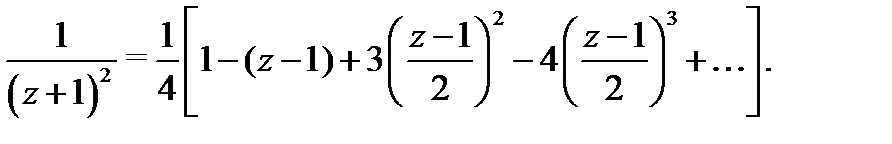
Подставляя найденные разложения в формулу (6), получаем представление функции 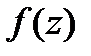в кольце 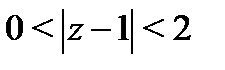в виде ряда Лорана:

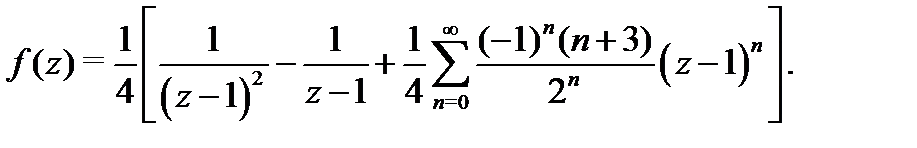
Пример 3.Разложить в ряд Лорана функцию 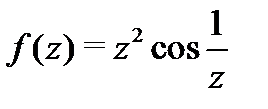в окрестности точки .

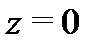Решение.Используем разложение (см. таблицу 1) 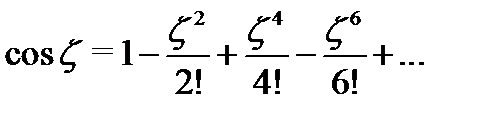. Полагая здесь 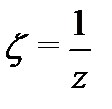, будем иметь

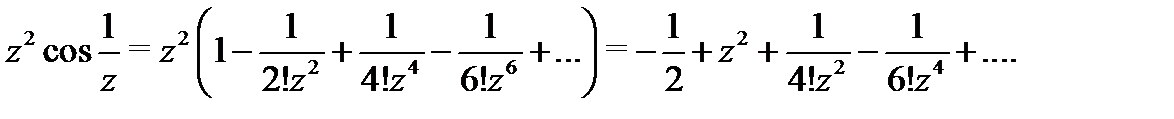
Это разложение справедливо для любой точки 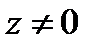. В данном случае кольцо представляет собой всю комплексную плоскость с одной выброшенной точкой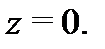

Пример 4.Разложить функцию

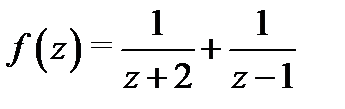
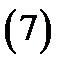
по степеням 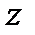в ряды Лорана с учетом ее особых точек.

Решение.Функция 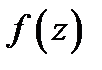имеет две особые точк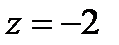и: и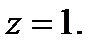

а) Разложение в круге 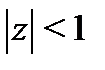. Преобразуем (7) следующим образом:

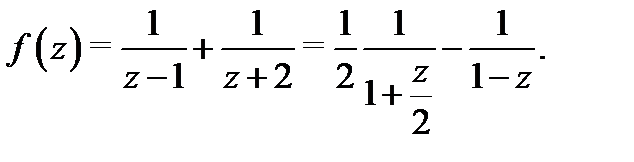
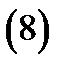
Используя формулу 1 из таблицы 1, получаем, что

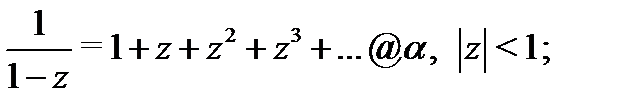
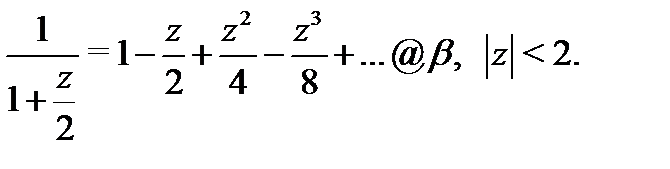
Подставляя эти разложения в (8), будем иметь

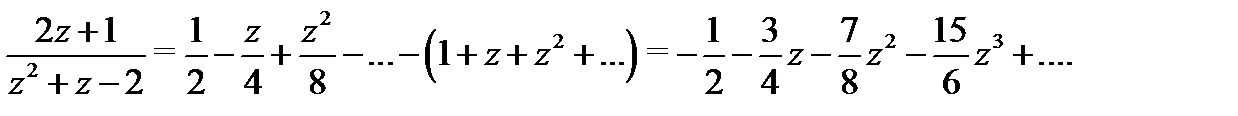
Это есть разложение в ряд Тейлора функции .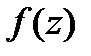

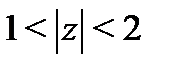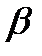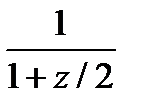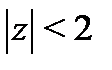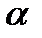б) Разложение в кольце . Ряд для функции остается сходящимся в этом кольце, так как . Ряд для функции 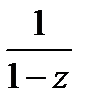расходится для 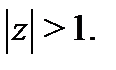Поэтому преобразуем 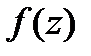следующим образом:

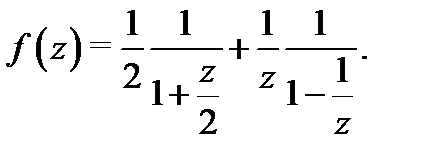
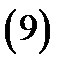
Применяя формулу 1 таблицы 1, будем иметь

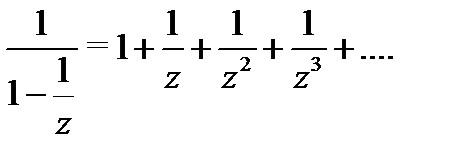
Этот ряд сходится, если 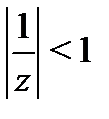, т.е. при 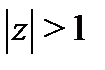. Подставляя это разложение и разложение 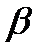в (9), найдем, что

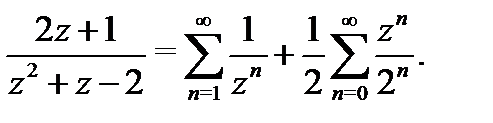
в) Разложение для 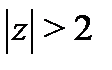. Функцию 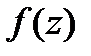представим в виде

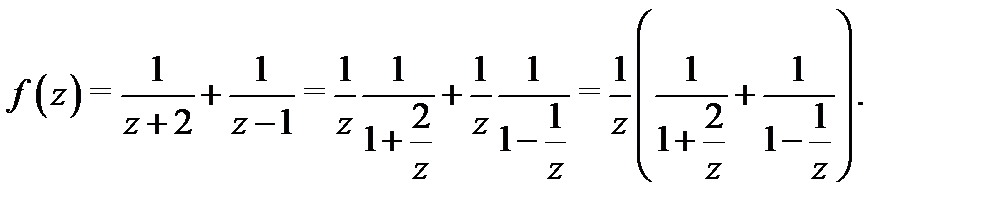
Тогда 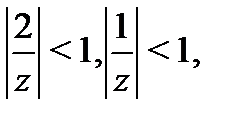так как 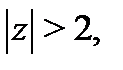поэтому можно применить формулу 1 таблицы 1 и получить, что

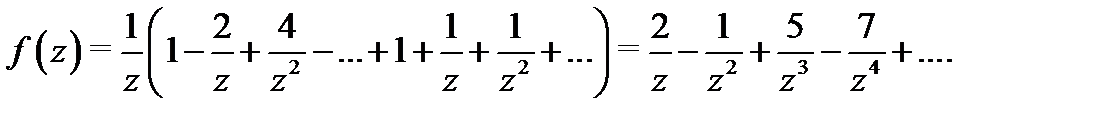
Пример 5.Разложить в ряд Лорана функцию 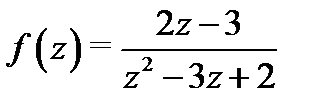в окрестности ее особых точек.

Решение. Особые точки функции : .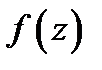

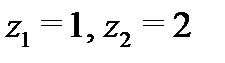а) Чтобы записать разложение функции 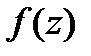в окрестности точки 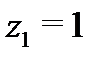, т.е. в кольце 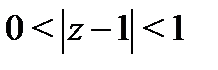, представим функцию 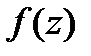в виде суммы простейших дробей:

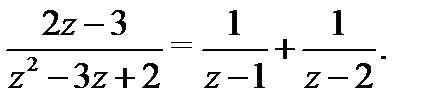
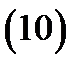
Правую часть (10) преобразуем следующим образом:

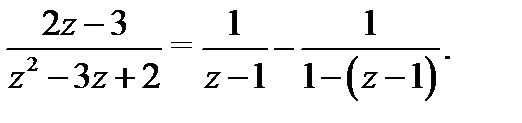
Применяя формулу 1 таблицы 1 (в которой 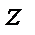заменим на 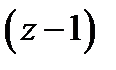), получим

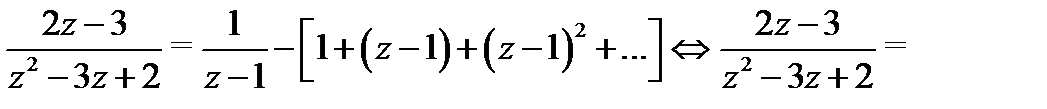
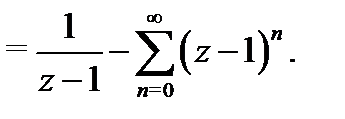
б) Разложение функции 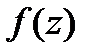в окрестности точки 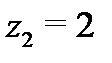, т.е. в кольце 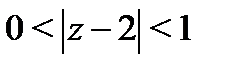, получим следующим образом:

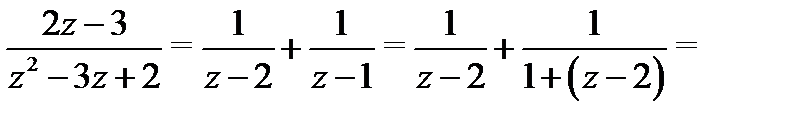
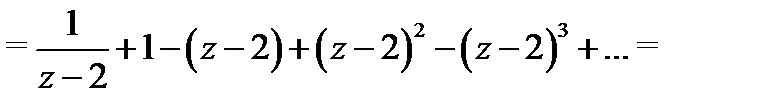
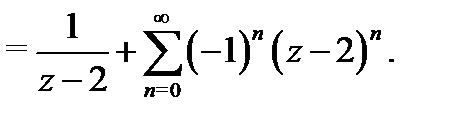
Установим теперь связь типа особой точки 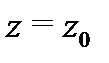функции 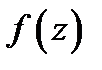с разложением этой функции в ряд Лорана в окрестности точки .

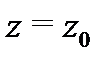Теорема 1. а) Точка 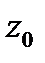является устранимой особой точкой функции 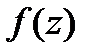тогда и только тогда, когда разложение этой функции в ряд Лорана в окрестности точки 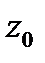не содержит главной части.

б) Точка 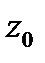является полюсом порядка 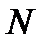функции 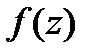тогда и только тогда, когда в разложении функции 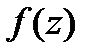в ряд Лорана в окрестности точки 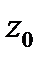главная часть разложения содержит конечное число членов, причем младшим отличным от нуля коэффициентом является .

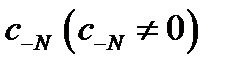в) Точка 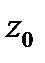является существенно особой точкой функции 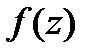тогда и только тогда, когда главная часть разложения функции в ряд Лорана в окрестности точки 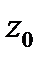содержит бесконечное число членов.

Доказательство проведем для утверждений а) и б). Разложим функцию 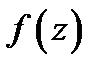в ряд Лорана в окрестности точки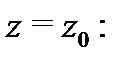

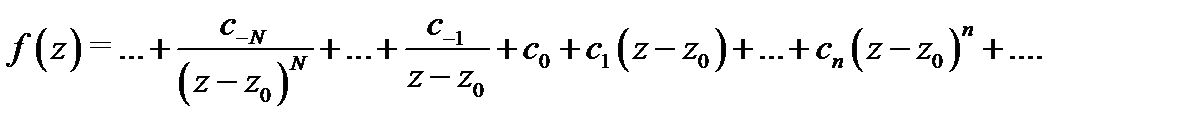
Устремляя здесь 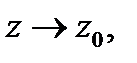видим, что конечный предел 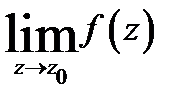существует тогда и только тогда, когда все 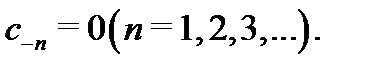При этом 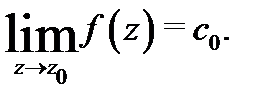Значит, точка 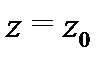будет устранимой особой точкой функции 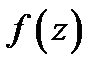тогда и только тогда, когда ряд Лорана (11) не содержит главной части. Утверждение а) доказано.

Умножим теперь обе части равенства (11) на 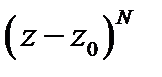. Получим разложение

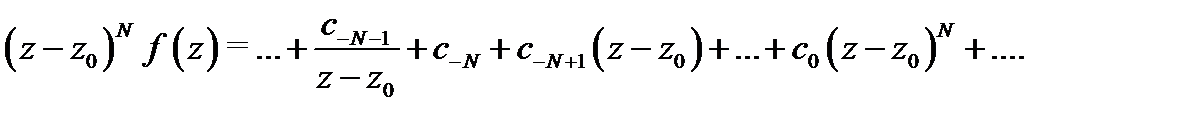
Отсюда видно, что конечный предел 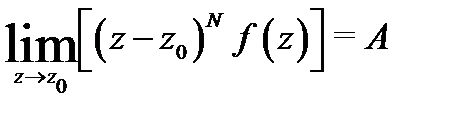существует тогда и только тогда, когда 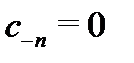для всех 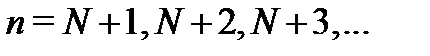. Это означает, что точка 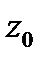является полюсом порядка 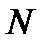функции 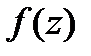тогда и только тогда, когда в разложении функции 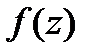в ряд Лорана в окрестности точки 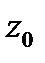главная часть разложения содержит конечное число членов, причем младшим отличным от нуля коэффициентом является 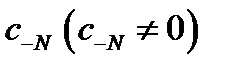, т.е. верно утверждение б). Теорема доказана.

2. Нули аналитической функции и их связь с полюсами

Определение 1. Точка 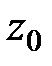называется нулём аналитической функции 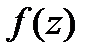порядка (или кратности) 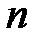, если

.

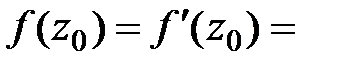
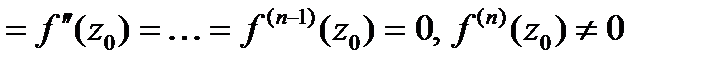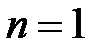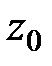В случае точка называется простым нулём.

Имеет место следующее почти очевидное утверждение.

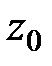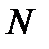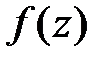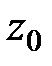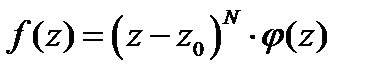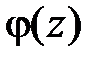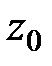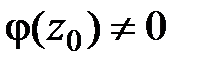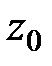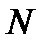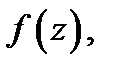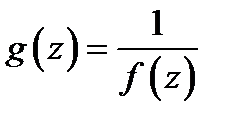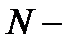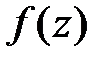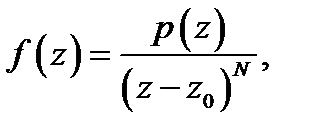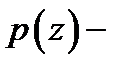Теорема 2. Для того, чтобы точка была нулем - гo порядка функции , аналитической в точке , необходимо и достаточно, чтобы в некоторой окрестности этой точки имело место равенство , где аналитична в точке и . Для того, чтобы точка была полюсом порядка функции необходимо и достаточно, чтобы функция имела в этой точке нуль го порядка. В этом случае представляется в виде где аналитическая в точке 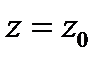функция, причем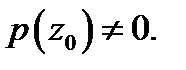

Пример 1. Найти нули функции 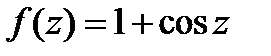и определить их порядки.

Решение. Из уравнения 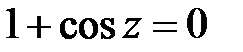находим точки 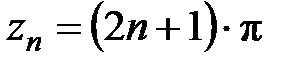, 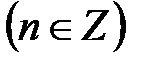– нули данной функции. Имеем: 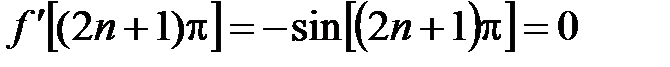, , 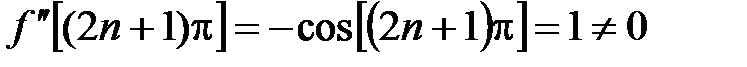т.е. точки 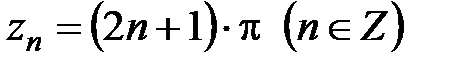– нули второго порядка данной функции.

Пример 2. Найти нули функции 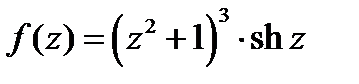и определить их порядки.

Решение.Полагая 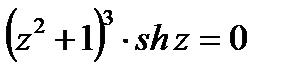, получаем, что 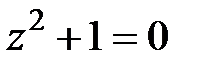или 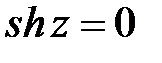. Решая эти уравнения, находим нули функции 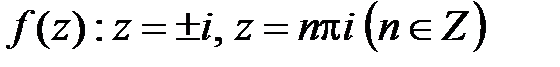. Пусть 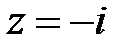; тогда 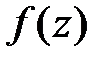можно представить в виде 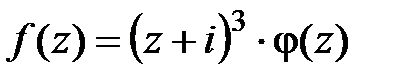, где функция 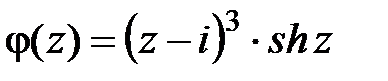является аналитическойв точке 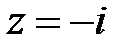, причем 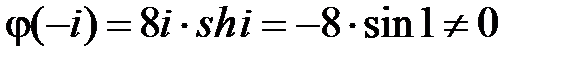. Это означает, что точка 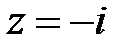есть нуль третьего порядка.Аналогично доказывается, что и точка 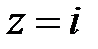является нулем третьего порядка. Исследуем нули 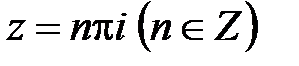. Производная 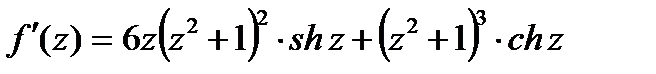в точках 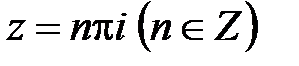отлична от нуля. Следовательно, 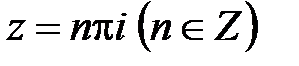– простые нули функции .

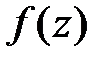Мы знаем структуру разложения функции 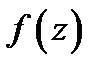в окрестности устранимой особой точки, в окрестности полюса и в окрестности существенно особой точки (см. теорему 1). Каким будет поведение функции 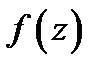при стремлении 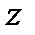к существенно особой точке 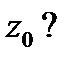Может ли она стремиться к какому-нибудь пределу, 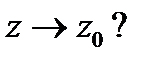Оказывается нет. Доказано следующее утверждение.

Теорема Сохоцкого.Если 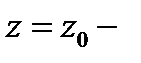существенно особая точка функции 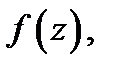то каково бы ни было наперёд заданное число 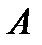( 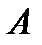может быть равным 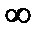), существует последовательность 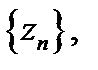стремящаяся к 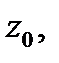такая, что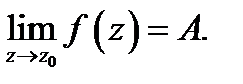

3. Вычеты. Теорема Коши о вычетах

Как ни странно, но именно особые точки интересны в приложениях. С помощью них удается решить многие задачи, например задачу о вычислении сложных несобственных интегралов (см. ниже). В основе этих вычислений лежит теория вычетов, к изучению которой мы переходим.

Определение 3. Пусть 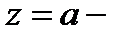изолированная особая точка функции 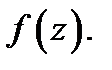Число

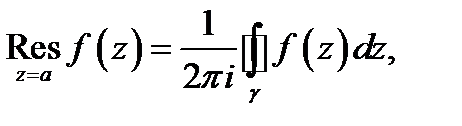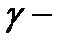где любой кусочно-гладкий замкнутый контур, лежащий в окрестности 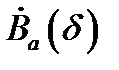аналитичности функции 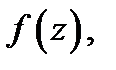обходимый против часовой стрелки и охватывающий точку 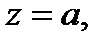называется вычетом функции 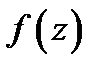в точке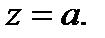

Вспоминая теорему Лорана, видим, что 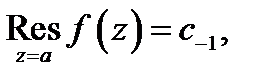т.е. равен коэффициенту при 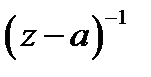в разложении функции 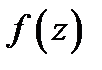в окрестности особой точки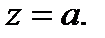

Теорема Коши о вычетах. Пусть функция 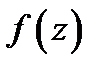аналитична в односвязной области 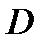и на её кусочно-гладкой замкнутой границе 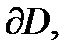за исключением конечного числа особых точек

Рис.13 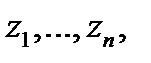лежащих внутри области 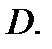Тогда

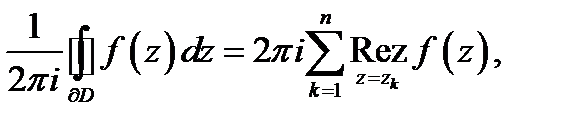
где граница 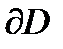обходится против часовой стрелки.

Доказательство.Окружим особые точки 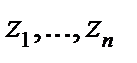попарно не пересекающимисязамкнутыми кусочно-гладкими контурами 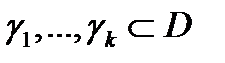(это всегда можно сделать, так как все особые точки изолированные). Обозначим через 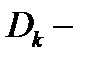область, охватываемую контуром 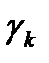(см. рис. 13). Тогда область 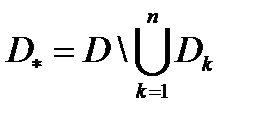будет 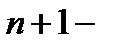связной. По теореме Коши для многосвязной области имеем 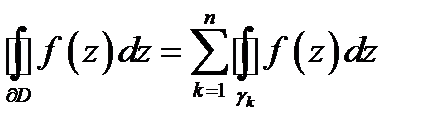(здесь все контуры обходятся против часовой стрелки). Так как 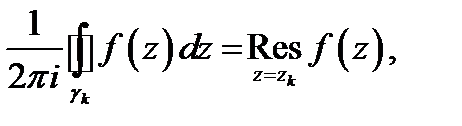тоимеет место равенство 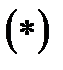. Теорема доказана.

На следующей лекции будут даны формулы вычисления вычетов и их их приложения.