Лекция 14. Системы линейных дифференциальных уравнений

Если в дифференциальной системе 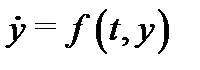правая часть 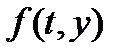линейна по 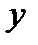, то эта система называется линейной системой дифференциальных уравнений. Такая система имеет вид

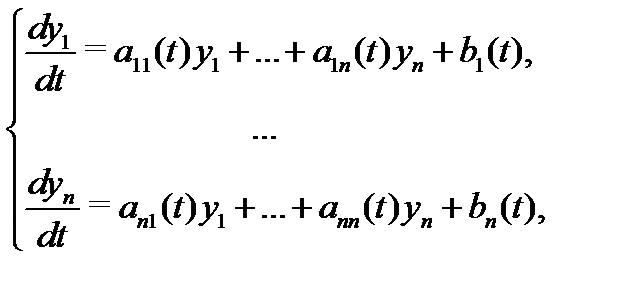
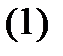
где 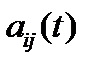и – и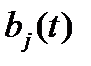звестные функции, 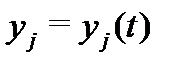– неизвестные функции ( 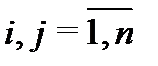). Пользуясь векторно-матричными обозначениями, систему (1) можно записать в следующей компактной форме:

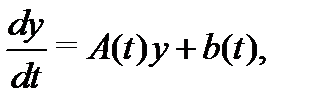
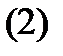
где

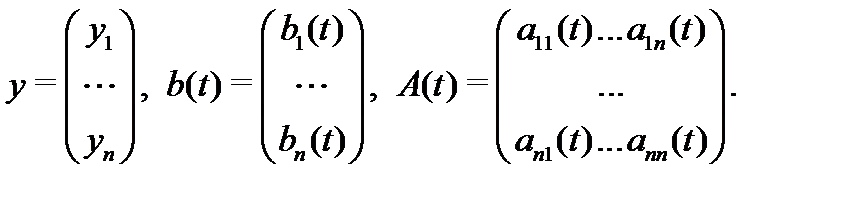
Мы будем пользоваться преимущественно записью (2). При этом число компонент неизвестной вектор-функции 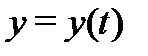(или размерность матрицы 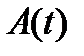) называется порядком системы (2). Таким образом, (2) – дифференциальная система 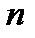-го порядка.

Вектор-функция 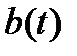называется неоднородностью системы (2). Если 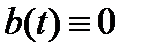(т.е. если все компоненты 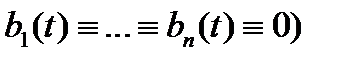, то система (2) называется однородной; в противном случае (т.е. если 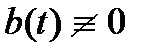) система (2) называется неоднородной системой. Если в (2) отбросить неоднородность, то получим соответствующую ей однородную систему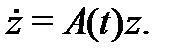

Оператор 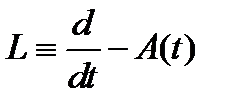позволяет записать систему (2) кратко так: 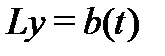. Изучим свойства этого оператора. Будем обозначать через 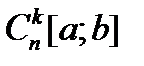пространство 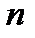-мерных вектор-функций 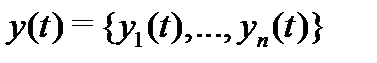, непрерывных на отрезке 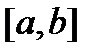вместе с производными 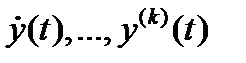до 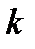-го порядка включительно (часто индекс 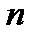в 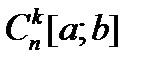опускают, если из контекста ясно, о каких вектор-функциях идет речь). Имеют место следующие утверждения.

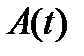Если матрица непрерывна на отрезке 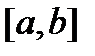(т.е. если все ее элементы 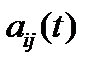непрерывны на 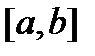), то оператор 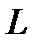действует из пространства 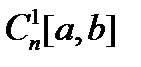в пространство 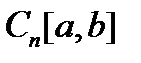непрерывных на отрезке 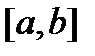вектор-функций:

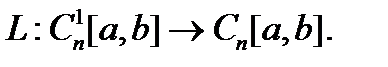
Оператор 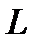линеен, т.е.

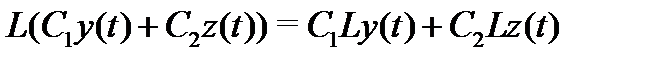
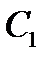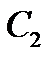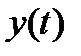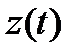для произвольных чисел и и произвольных элементов и пространства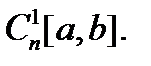

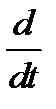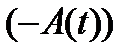Первое свойство вытекает из того, что при дифференцировании гладкость функции понижается на единицу, а второе свойство вытекает из того, что операторы и являются линейными операторами, а значит линейным оператором является и их сумма .

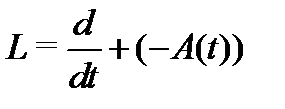Если через 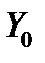обозначить пространство решений однородной системы уравнений 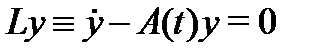c непрерывной матрицей 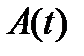, то из свойств и сразу же вытекает, что 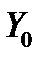– линейное пространство. Как и в случае скалярных дифференциальных уравнений, нас будет интересовать, какова размерность пространства 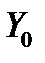и какие системы функций образуют в нем базис. Мы ответим на эти вопросы, если научимся выделять в 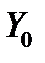максимальную линейно независимую систему элементов.

1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений

Пусть 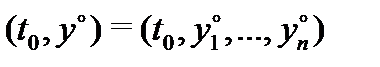– фиксированный постоянный вектор в 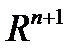. Рассмот-

рим начальную задачу

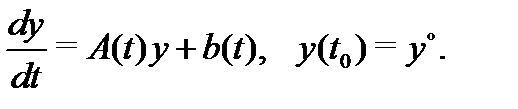
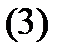
Имеет место следующее утверждение.

Теорема 1. Если в системе (2) матрица 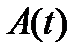и вектор-функция 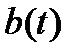непрерывны на отрезке 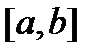, то какова бы ни была начальная точка 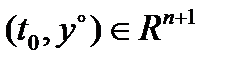, задача Коши (3) имеет решение 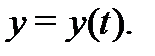Это решение единственно и определено на отрезке .

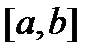Таким образом, в случае линейной системы дифференциальных уравнений разрешимость начальной задачи глобальная: решение существует там, где непрерывна правая часть дифференциальной системы. В случае нелинейных систем это не так.

Пример 1. Показать, что задача Коши

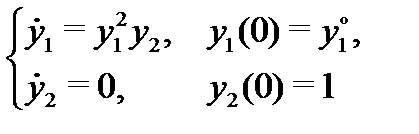
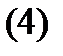
с непрерывными (при всех 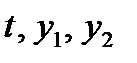) правыми частями не имеет решение, определенное при всех 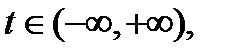если .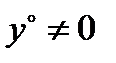

Решение. Из второго уравнения (4) находим, что 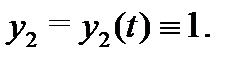Поэтому первое уравнение приобретает вид

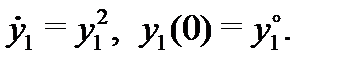
Разделяя здесь переменные, будем иметь

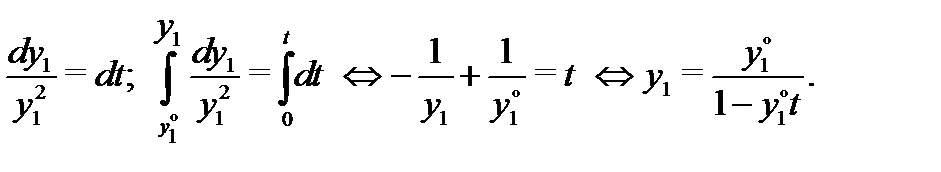
Итак, задача Коши (4) имеет следующее решение:

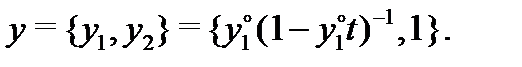
Это решение единственно, так как выполнены все условия теоремы Коши. Первая компонента решения разрывна при ( 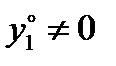), поэтому каково бы ни было начальное значение 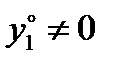, решение (5) не может существовать на всей оси 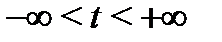, так как оно всегда разрывно в точке .

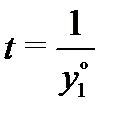2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений

Эти понятия встречались при изучении скалярных дифференциальных уравнений. На вектор-функции они обобщаются следующим образом.

Определение 3. Система вектор-функций

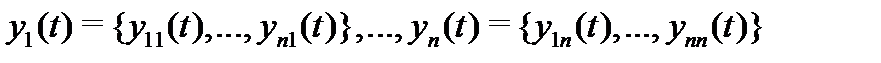
называется линейно зависимой на отрезке 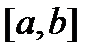, если существуют числа 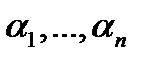, не равные нулю одновременно, такие, что для всех 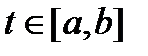имеет место тождество

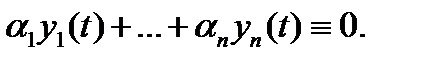
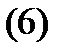
Если же тождество (6), где 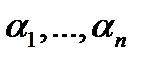– числа, имеет место тогда и только тогда, когда все 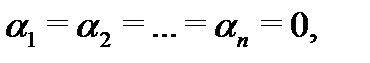то система вектор-функций 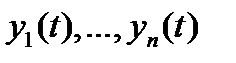называется линейно независимой на отрезке .

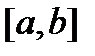Заметим, что векторное тождество (6) эквивалентно 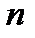скалярным тождествам

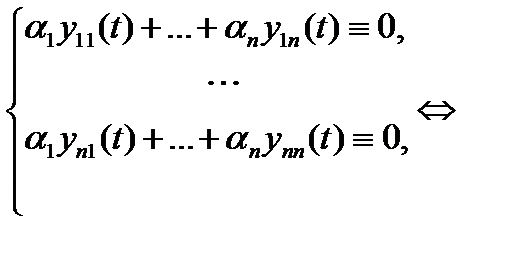
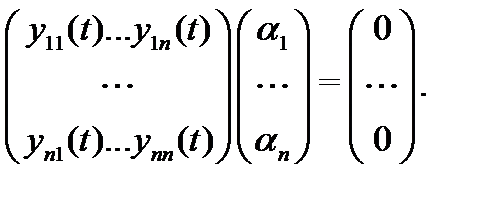
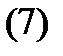
Определение 4. Определитель

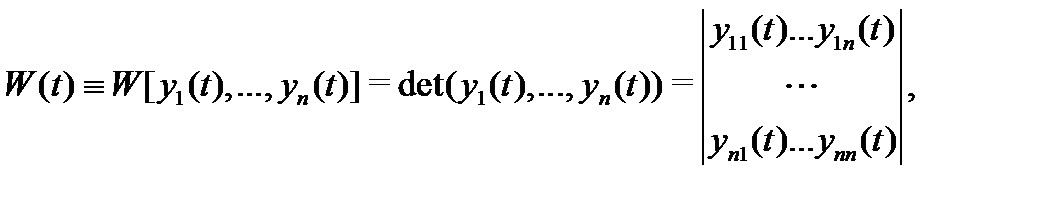
столбцами которого являются вектор-функции 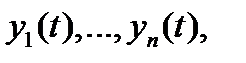называется определителем Вронского (или вронскианом) системы вектор-функций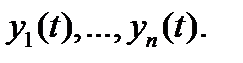

Теорема 2 (необходимое условие линейной зависимости). Если система вектор-функций 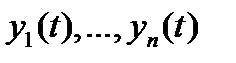линейно зависима на отрезке 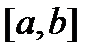, то их вронскиан 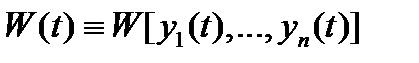тождественно обращается в нуль на этом отрезке, т.е. .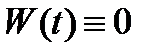

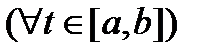Доказательство. Так как вектор-функции 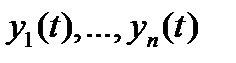линейно зависимы на отрезке 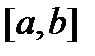, то существуют числа 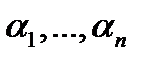, не равные нулю одновременно, такие, что имеет место тождество (6). Но это означает, что эквивалентная им линейная система (7) алгебраических уравнений имеет при всех 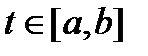нетривиальное решение 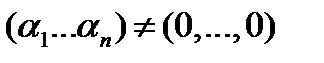. Это возможно лишь в том случае, когда определитель системы (7) обращается в нуль при всех 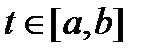. Остается заметить, что указанный определитель совпадает с вронскианом системы функций 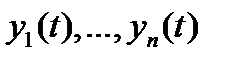. Теорема доказана.

Следствие 1. Если вронскиан 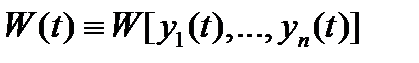не обращается в нуль хотя бы в одной точке 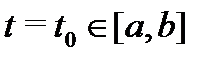, то система вектор-функций 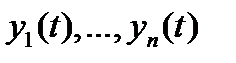линейно независима на отрезке 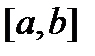(если, конечно, она имеет смысл на этом отрезке).

Как и в скалярном случае, из тождества 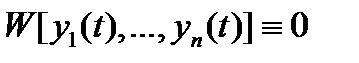еще не следует, что система вектор-функций 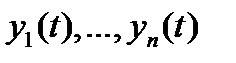линейно зависима на отрезке 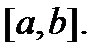Например, вектор-функции

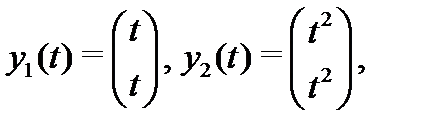
линейно независимы на любом отрезке (докажите это!), а их вронскиан

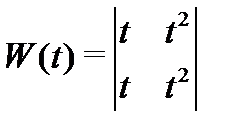
тождественно равен нулю на отрезке . Однако для системы решений однородной системы

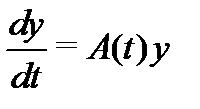
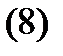
с непрерывной на отрезке 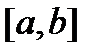матрицей теорему 2 можно обратить.

Теорема 3. Пусть 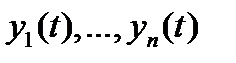– система решений однородной дифференциальной системы (8) с непрерывной на отрезке 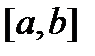матрицей 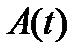. Тогда имеют место следующие утверждения:

1) решения 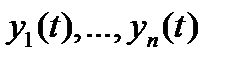линейно независимы на отрезке 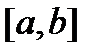тогда и только тогда, когда их вронскиан 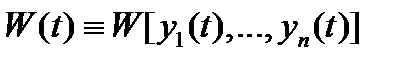нe обращается в нуль ни в одной точке отрезка ;

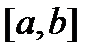2) решения 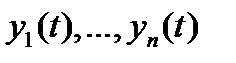линейно зависимы на отрезке 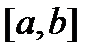тогда и только тогда, когда их вронскиан 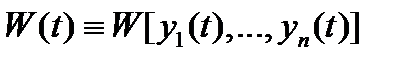тождественно равен нулю на отрезке .

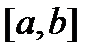Докажем, например, утверждение 1). Достаточность его очевидна, так как если 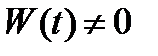хотя бы в одной точке 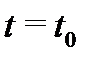отрезка 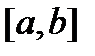, то из следствия 1 вытекает, что функции 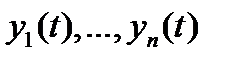линейно независимы на отрезке 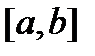. Докажем необходимость.

Пусть решения 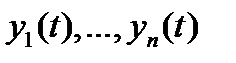системы (8) линейно независимы на отрезке 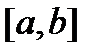. Предположим, что существует точка 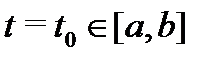такая, что 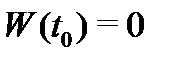. Отсюда следует, что столбцы 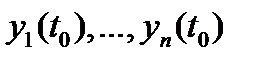определителя 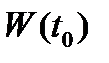линейно зависимы, т.е. существуют числа 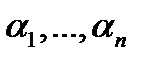, не равные нулю одновременно, такие что

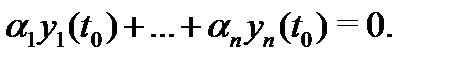
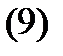
Рассмотрим вектор-функцию 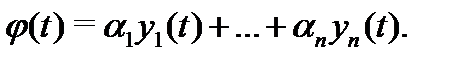В силу линейности пространства 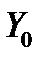решений однородной системы (8) эта функция является решением указанной дифференциальной системы. Из (9) следует, что она удовлетворяет начальному условию 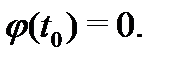Но такому же начальному условию удовлетворяет и тривиальное решение 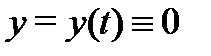системы (8). В силу единственности решения вектор-функци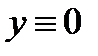и и 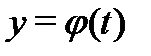совпадают на отрезке 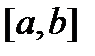, т.е.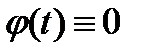 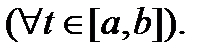Следовательно,

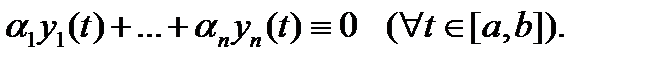
Поскольку здесь числа 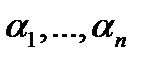не равны нулю одновременно, то это означает, что решения 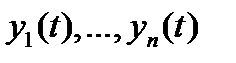линейно зависимы на отрезке 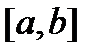, чего не может быть. Значит, равенство 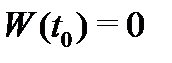ложно, поэтому 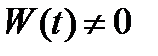при всех 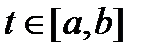. Теорема доказана.

Из этой теоремы вытекают следующие свойства вронскиана 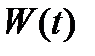системы решений 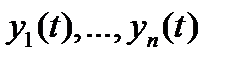однородной диффернциальной системы (8) с непрерывной на отрезке 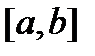матрицей :

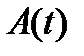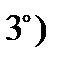если вронскиан 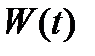обращается в нуль хотя бы в одной точке 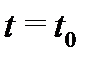отрезка 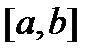, то ;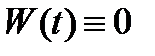

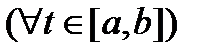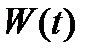если вронскиан не равен нулю хотя бы в одной точке 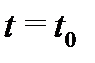отрезка 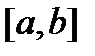, то он не равен нулю на всем отрезке .

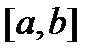Эти свойства становятся очевидными, если воспользоваться формулой Лиувилля

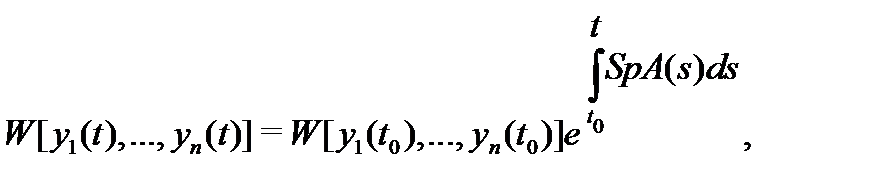
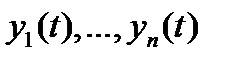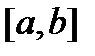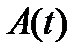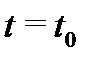где – решения однородной системы (8) с непрерывной на отрезке матрицей , а – произвольная фиксированная точка этого отрезка. Через 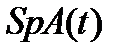обозначен след матрицы 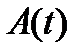, т.е. сумма всех ее элементов 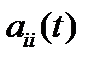, стоящих на главной диагонали: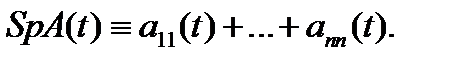

3. Фундаментальная матрица решений и структура общего решения однородной системы

Рассмотрим однородную систему (8). Пусть она имеет порядок 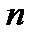. Введем следующее важное понятие.

Определение 5. Матрица

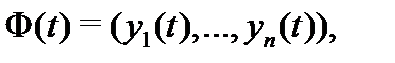
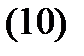
столбцами которой являются 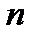линейно независимых на отрезке 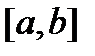решений 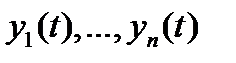системы (8), называется фундаментальной матрицей решений системы (8) (на отрезке ).

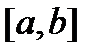Заметим, что поскольку каждый столбец 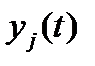матрицы 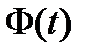удовлетворяет системе (8), то фундаментальная матрица решений удовлетворяет матричному дифференциальному уравнению

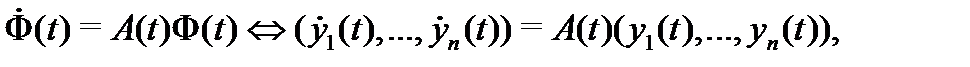
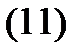
которое эквивалентно 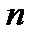векторным уравнениям

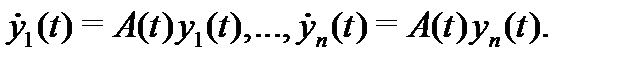
С помощью фундаментальной матрицы решений можно записать общее решение однородной системы (8). Сначала докажем следующее утверждение.

Теорема 4. Для любой однородной системы (8) с непрерывной на отрезке 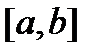матрицей 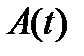существуют (и даже бесчисленное множество) фундаментальные матрицы решений .

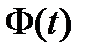Доказательство. Пусть 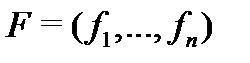– произвольная постоянная матрица с 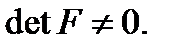Возьмем в качестве начальных векторов столбцы 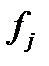этой матрицы и рассмотрим 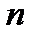задач Коши:

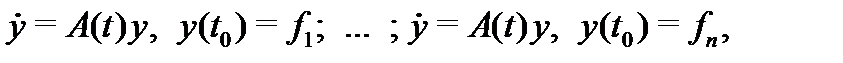
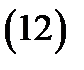
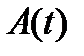где – произвольная фиксированная точка отрезка . Так как матрица непрерывна на отрезке 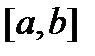, то задачи (12) имеют решения 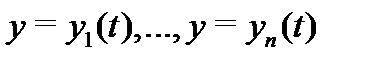на отрезке 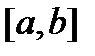и эти решения единственны (см. теорему 1). Составим из этих решений матрицу (10). Она является фундаментальной матрицей решений (на отрезке 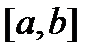) однородной дифференциальной системы (8). Действительно, каждый ее столбец является решением системы (8) (по построению задач Коши (12)) и 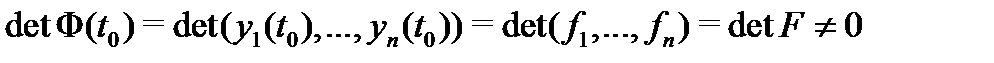(в силу выбора матрицы 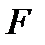). Значит, столбцы матрицы 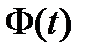линейно независимы на отрезке 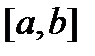(см. следствие 1). Теорема доказана.

Теорема 5. Пусть в однородной дифференциальной системе (8) матрица 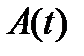непрерывна на отрезке 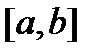. Тогда ее общее решение имеет вид

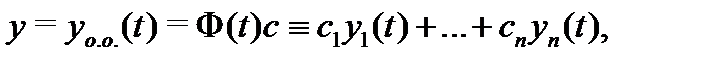
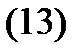
где 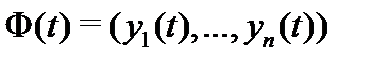– фундаментальная (на отрезке 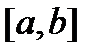) матрица решений системы (8), а 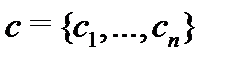– произвольный постоянный вектор.

Доказательство. Дифференцируя (13) по 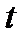и, учитывая, что матрица 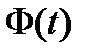удовлетворяет уравнению 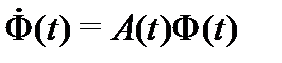, будем иметь

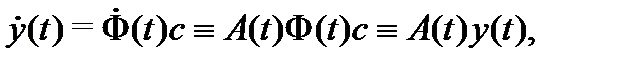
т.е. вектор-функция (13), является решением системы (8) при любом постоянном векторе 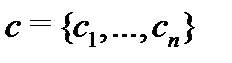. Если теперь 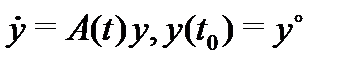– произвольная задача Коши для системы (8) ( 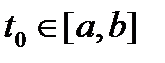, 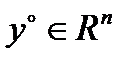), то подчиняя функцию (13) начальному условию 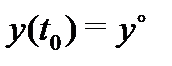найдем, что

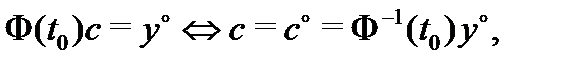
а значит, вектор-функция (13), где 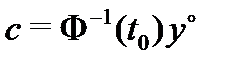удовлетворяет указанной задаче Коши. Следовательно, (13) – общее решение системы (8). Теорема доказана.

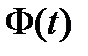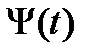Пусть и – две фундаментальные матрицы решений дифференциальной системы (8). Как связаны они между собой? Связь эта очень проста и описывается следующим утверждением.

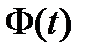Если и 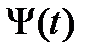– две фундаментальные (на отрезке 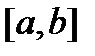) матрицы решений однородной системы (8) с непрерывной на отрезке 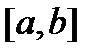матрицей 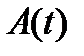, то существует постоянная матрица 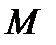такая, что 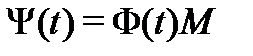. При этом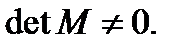

Действительно, в силу теоремы 5 каждый столбец 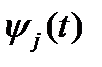матрицы 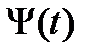, являясь решением системы (8), имеет вид 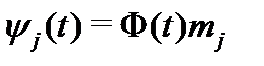, где 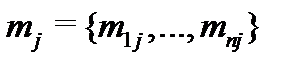– некоторый постоянный вектор. Поэтому матрица 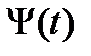может быть записана в форме 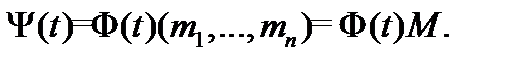Матрица 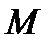не вырождена, так как если бы 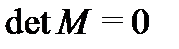, то 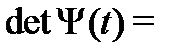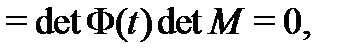чего не может быть в силу фундаментальности матрицы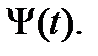

4. Структура общего решения неоднородной системы дифференциальных уравнений

Рассмотрим теперь неоднородную дифференциальную систему

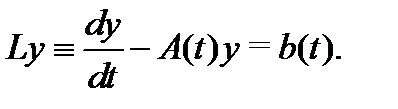
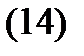
Теорема 6. Пусть в системе (14) матрица 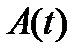и вектор-функция 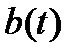непрерывны на отрезке 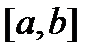и пусть 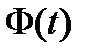– фундаментальная матрица решений соответствующей однородной системы 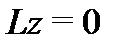. Тогда общее решение неоднородной дифференциальной системы (14) имеет вид

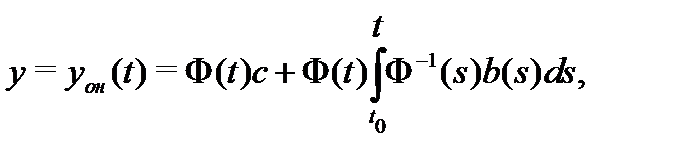
где 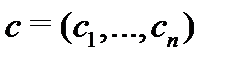– произвольный постоянный вектор, – произвольная (фиксированная) точка отрезка .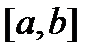

Доказательство. Применяя к (15) оператор 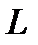, учитывая его линейность и тот факт, что 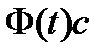– общее решение соответствующей однородной системы 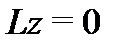, будем иметь

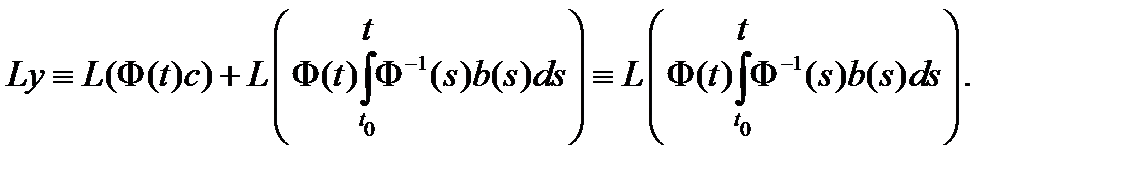
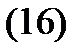
Вычислим теперь

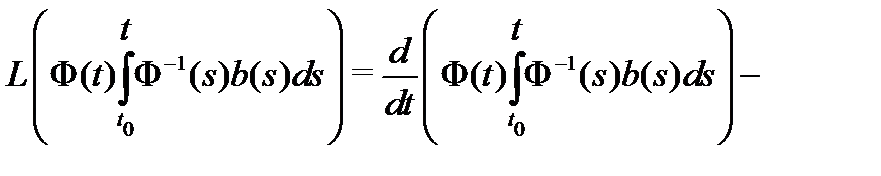
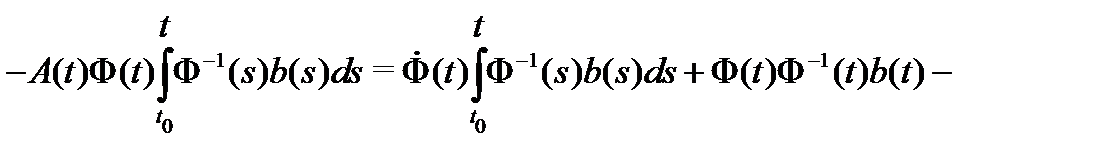
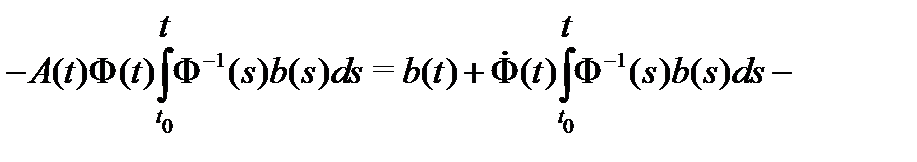
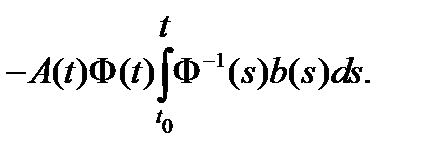
Учитывая, что 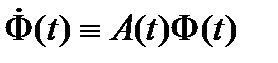, получаем из (16) тождество

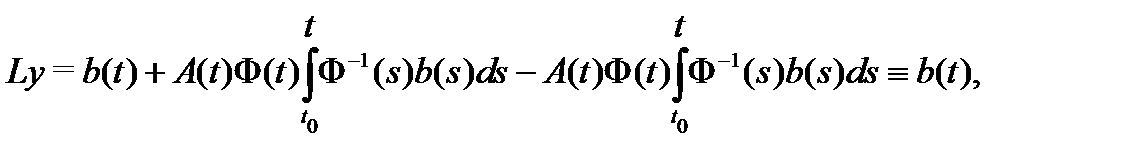
которое показывает, что вектор-функция (15) является решением неоднородной системы (14) при любом постоянном векторе .

Если теперь 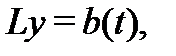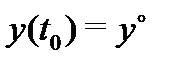– произвольная задача Коши для системы (14), то подчиняя функцию (15) начальному значению 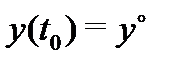, получаем 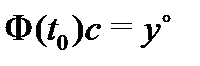, откуда найдем 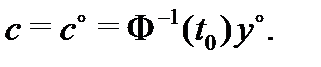Следовательно, вектор-функция (15), где 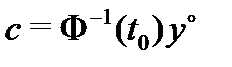, является решением указанной задачи Коши. Это означает, что (15) – общее решение дифференциальной системы (14). Теорема доказана.

Следствие 2. Решением задачи Коши

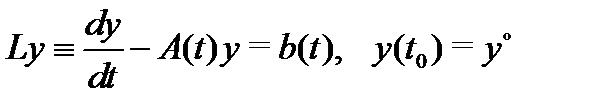
(с непрерывными на отрезке 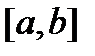матрицей 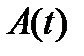и неоднородностью 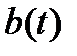) является вектор-функция

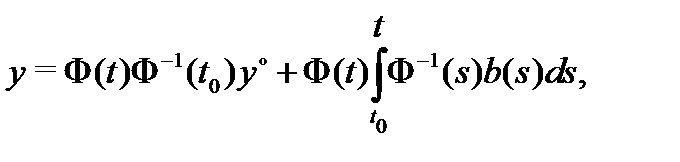
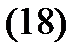
где 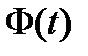– фундаментальная матрица решений соответствующей однородной системы , .

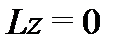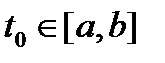Это вытекает из заключительной части доказательства теоремы 6. Заметим, что формулу (18) называют формулой Коши решения начальной задачи (17) для неоднородной дифференциальной системы (14).

Пример 5. Найти общее решение системы

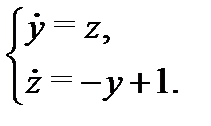
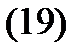
Решение. Построим сначала фундаментальную матрицу решений соответствующей однородной системы 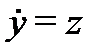, 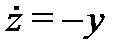. Применяя метод исключения (см. разд. 2), приведем эту систему (дифференцированием по 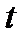первого уравнения) к скалярному уравнению второго порядка:

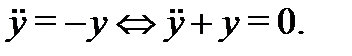
Общее решение этого уравнения (см. пример 3) имеет вид

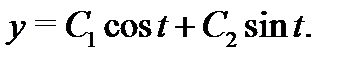
Учитывая, что 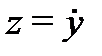, получаем общее решение однородной системы , :

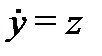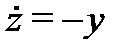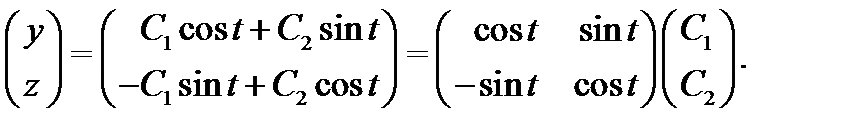
Стоящая здесь матрица

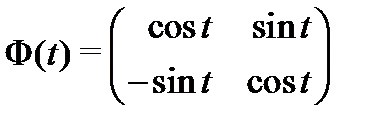
является фундаментальной матрицей решений для однородной системы 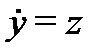, 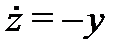(проверьте это, используя определение 5). По формуле Коши (18) вычисляем общее решение системы (19):

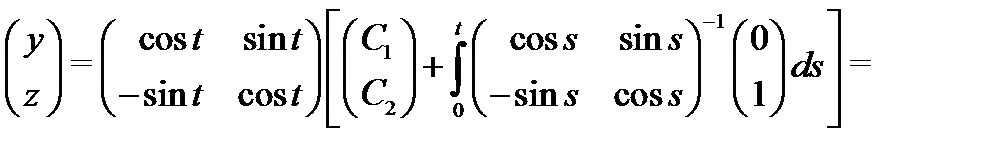
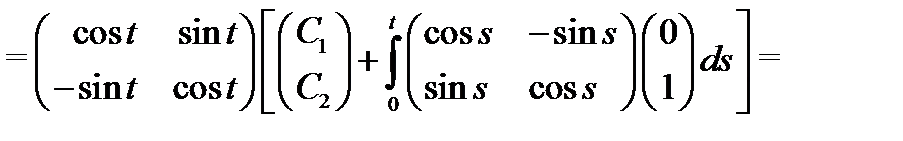
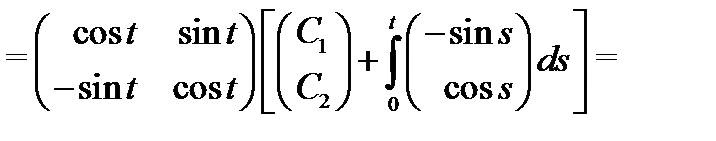
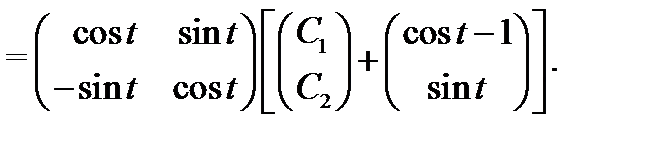
Теперь, когда изучена структура общего решения линейной дифференциальной системы, можно вычислить размерность пространства 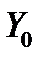решений однородной системы (8) и выделить в нем базис.

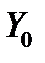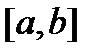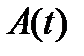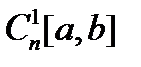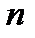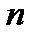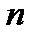Следствие 3. Пространство решений однородной системы (8) с непрерывной на отрезке матрицей является подпространством пространства размерности (где – размерность (порядок) системы (8)). В качестве базиса пространства можно взять любые линейно независимых решений системы (8) (или 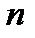столбцов любой ее фундаментальной матрицы решений ).

Заметим, что пространство решений неоднородной системы 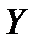не является линейным пространством, если 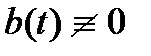. Оно получается из пространства 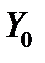решений однородной системы (8) сдвигом на вектор 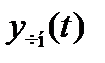, являющийся частным решением неоднородной системы (14), т.е. 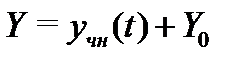, так как 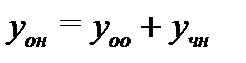(см. (15)).