Лекция 13. Системы дифференциальных уравнений. Общие понятия
Совокупность двух или более дифференциальных уравнений называется системой дифференциальных уравнений. Примеры таких систем приводились в лекции 1. Заметим, что в случае систем обычно обозначают независимую переменную буквой 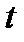 , рассматривая ее как время. Например, уравнения
, рассматривая ее как время. Например, уравнения
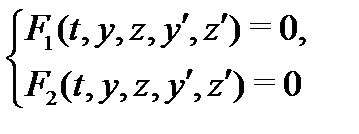
образуют систему двух уравнений с двумя неизвестными функциями 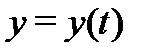 и
и 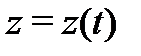 . Если система записана в виде уравнений
. Если система записана в виде уравнений
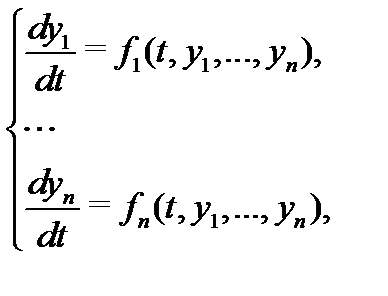
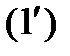
то ее называют системой, разрешенной относительно всех производных, или системой уравнений в нормальной форме. Вводя в рассмотрение векторы  и
и 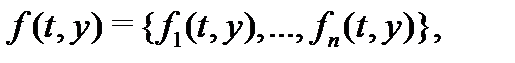 то систему
то систему 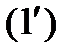 можно записать кратко так:
можно записать кратко так:
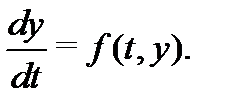
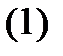
Такая форма записи системы уравнений 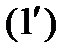 называется ее векторной формой. Ею мы и будем пользоваться в дальнейшем.
называется ее векторной формой. Ею мы и будем пользоваться в дальнейшем.
1. Понятия общего и частного решений. Задача Коши и ее разрешимость
Областью определения системы (1) называется область определения ее правой части 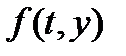 , т.е. множество
, т.е. множество

Например, областью определения системы
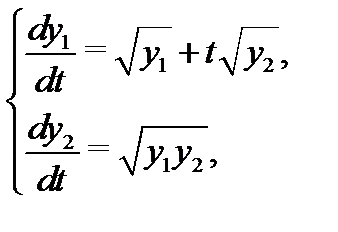
является множество
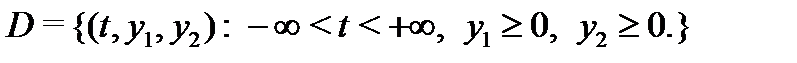
В левой части системы (1) стоит производная вектор-функции 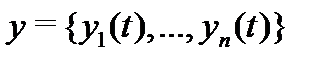 скалярного аргумента
скалярного аргумента  . В дальнейшем будут встречаться и интегралы от вектор-функции. Поэтому с самого начала разъясним соответствующие понятия.
. В дальнейшем будут встречаться и интегралы от вектор-функции. Поэтому с самого начала разъясним соответствующие понятия.
Производная (любого порядка) вектор-функции скалярного аргумента определяется равенствами:
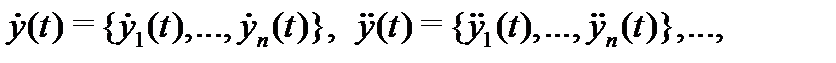
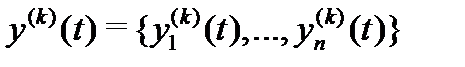
(здесь 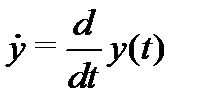 ), а интеграл – равенством
), а интеграл – равенством
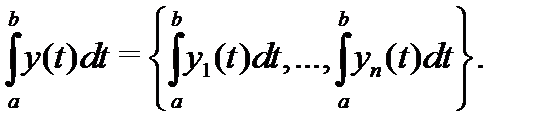
Таким образом, чтобы продифференцировать или проинтегрировать вектор-функцию скалярного аргумента, надо продифференцировать или проинтегрировать каждую компоненту этой функции. Вектор-функция называется непрерывной в точке 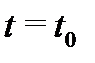 (или на множестве
(или на множестве  ), если непрерывна в этой точке (или на множестве
), если непрерывна в этой точке (или на множестве  ) каждая компонента этой функции. Для вектор-функций скалярного аргумента сохраняются обычные правила дифференцирования:
) каждая компонента этой функции. Для вектор-функций скалярного аргумента сохраняются обычные правила дифференцирования:
а) 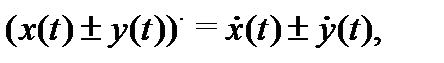
б) 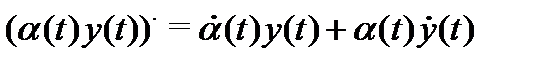 (
( 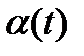 – скалярная функция),
– скалярная функция),
в) 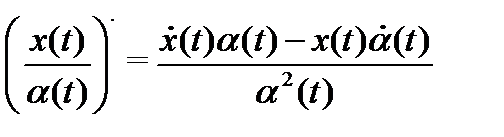 (
( 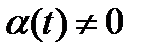 – скалярная функция),
– скалярная функция),
г) 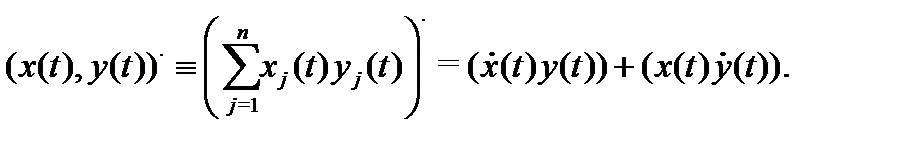
Интеграл от вектор-функции обладает свойствами линейности, аддитивности, дифференцируемости по верхнему и нижнему пределам. Например,
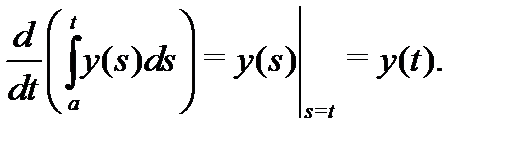
Имеет место оценка
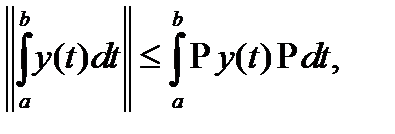
где 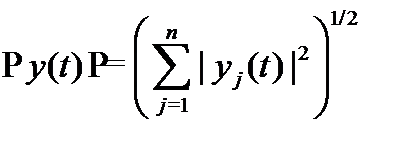 или
или 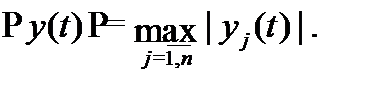
Если производную от матрицы 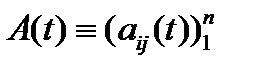 определить равенством
определить равенством  то, как нетрудно видеть, будут иметь место формулы
то, как нетрудно видеть, будут иметь место формулы
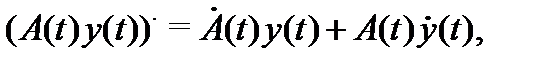

Перейдем к понятию решения системы (1). Пусть 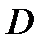 – область определения системы (1).
– область определения системы (1).
Определение 1. Решением системы дифференциальных уравнений (1) на отрезке 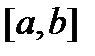 называется вектор-функция
называется вектор-функция 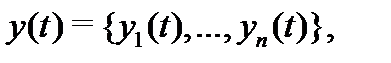 обладающая свойствами:
обладающая свойствами:
1) 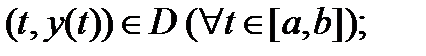
2) вектор-функция 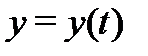 дифференцируема на отрезке
дифференцируема на отрезке 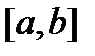 ;
;
3) при всех 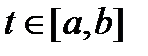 выполняется тождество
выполняется тождество
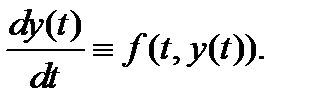
Аналогично определяются решения на промежутках 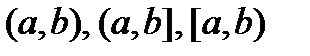 и
и 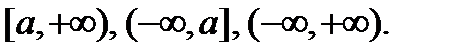 Если
Если 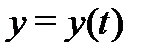 – решение системы (1) на отрезке
– решение системы (1) на отрезке 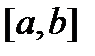 , то множество точек
, то множество точек 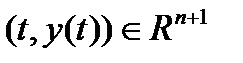 , когда
, когда 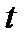 пробегает отрезок
пробегает отрезок 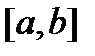 , образует в
, образует в 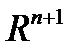 некоторую
некоторую 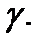 Эту кривую называют интегральной кривой системы (1). Пространство
Эту кривую называют интегральной кривой системы (1). Пространство 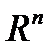 переменных
переменных 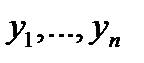 называют фазовым пространством. Проекция интегральной кривой
называют фазовым пространством. Проекция интегральной кривой 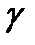 в фазовое пространство называется траекторией системы уравнений (1). Ясно, что по интегральной кривой
в фазовое пространство называется траекторией системы уравнений (1). Ясно, что по интегральной кривой 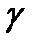 траектория определяется однозначно, но не наоборот. Впредь решение
траектория определяется однозначно, но не наоборот. Впредь решение 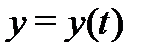 также будем называть интегральной кривой системы (1).
также будем называть интегральной кривой системы (1).
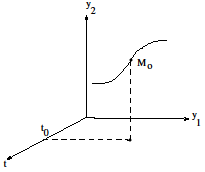 Мы знаем, что решение дифференциальных уравнений определяется неоднозначно. Чтобы выделить вполне конкретное решение, надо задать дополнительные условия. Пусть
Мы знаем, что решение дифференциальных уравнений определяется неоднозначно. Чтобы выделить вполне конкретное решение, надо задать дополнительные условия. Пусть 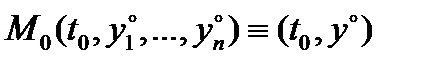 – фиксированная точка в области
– фиксированная точка в области 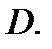 Задача, состоящая в нахождении решения
Задача, состоящая в нахождении решения 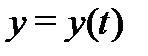 системы (1), удовлетворяющего начальному условию
системы (1), удовлетворяющего начальному условию 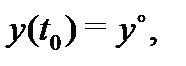 называется задачей Коши или начальной задачей для системы (1). Ее кратко Рис. 11 записывают так:
называется задачей Коши или начальной задачей для системы (1). Ее кратко Рис. 11 записывают так:
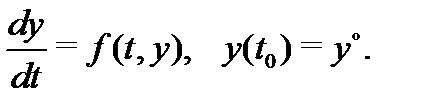
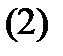
Ее геометрический смысл состоит в том, чтобы среди всех интегральных кривых системы (1) найти ту, которая проходит через заданную начальную точку 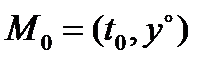 (см. рис. 11).
(см. рис. 11).
В каком случае задача Коши (2) имеет решение? Как и в случае скалярных дифференциальных уравнений это зависит от свойств правой части
Теорема Коши. Пусть все компоненты  правой части
правой части 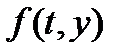 и их частные производные
и их частные производные 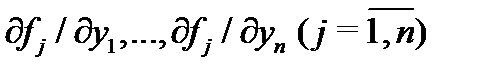 непрерывны в области
непрерывны в области 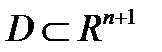 . Тогда какова бы ни была начальная точка
. Тогда какова бы ни была начальная точка 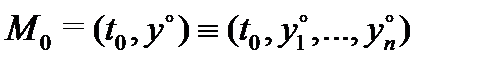 , лежащая внутри области
, лежащая внутри области 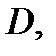 существует отрезок
существует отрезок 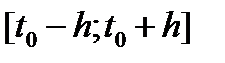 такой, что задача Коши (2) имеет решение на этом отрезке, причем это решение единственно.
такой, что задача Коши (2) имеет решение на этом отрезке, причем это решение единственно.
Отметим, что эта теорема носит локальный характер: существование решения 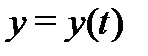 гарантируется лишь в достаточно малой окрестности точки
гарантируется лишь в достаточно малой окрестности точки 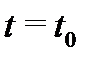 (
( 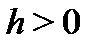 – достаточно мало). Кроме того, условия этой теоремы носят достаточный характер. При нарушении этих условий задача (2) может иметь или может не иметь решения. При этом, если решение существует, оно может быть не единственным. Например, задача Коши
– достаточно мало). Кроме того, условия этой теоремы носят достаточный характер. При нарушении этих условий задача (2) может иметь или может не иметь решения. При этом, если решение существует, оно может быть не единственным. Например, задача Коши
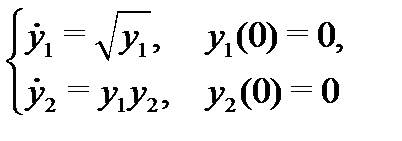
имеет два решения: 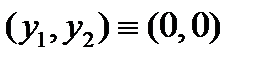 и
и 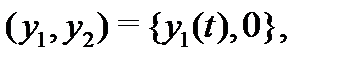 где
где  – функция вида
– функция вида
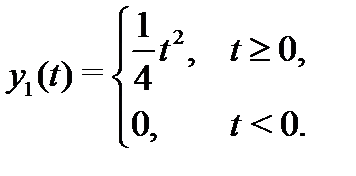
Нарушение единственности решения объясняется тем, что условия теоремы Коши здесь не выполнены (именно: частная производная 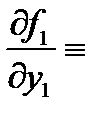
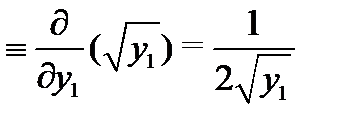 разрывна в начальной точке
разрывна в начальной точке 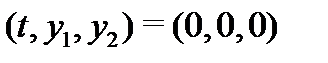 ).
).
Как и в случае скалярных уравнений, здесь также вводятся понятия частного и общего решений, частного и общего интегралов. Частным решением системы (1) называется решение 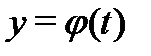 какой-нибудь ее задачи Коши (2) (именно: задачи Коши с начальным условием
какой-нибудь ее задачи Коши (2) (именно: задачи Коши с начальным условием 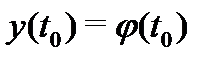 ).
).
Определение 2. Вектор-функция
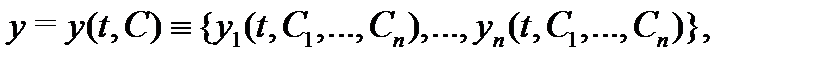
зависящая от 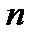 произвольных постоянных
произвольных постоянных 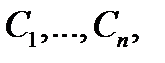 называется общим решением системы (1), если она удовлетворяет следующим требованиям:
называется общим решением системы (1), если она удовлетворяет следующим требованиям:
1) при любых допустимых значениях постоянных 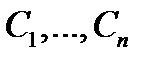 функция
функция 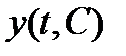 является решением системы (1) на каком-нибудь отрезке
является решением системы (1) на каком-нибудь отрезке 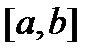 ;
;
2) какова бы ни была начальная точка 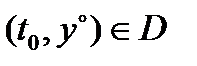 (
(  – область определения системы (1)), существуют значения
– область определения системы (1)), существуют значения 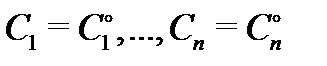 постоянных
постоянных  такие, что функция
такие, что функция 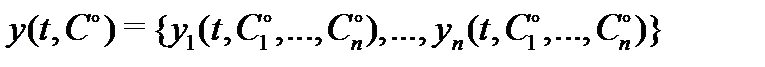 является решением задачи Коши (2) с начальной точкой
является решением задачи Коши (2) с начальной точкой 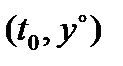 .
.
Условие 2) означает, что алгебраическая система уравнений
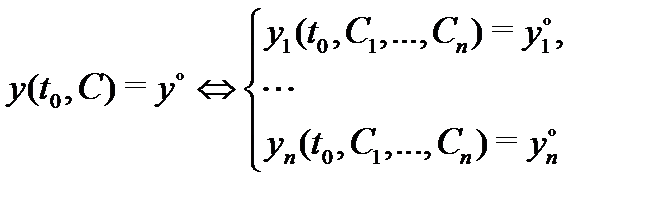
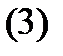
(относительно неизвестных 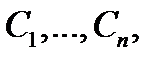 ) имеет хотя бы одно решение. Заметим, что в определении общего решения иногда требуют, чтобы указанная алгебраическая система уравнений имела единственное решение
) имеет хотя бы одно решение. Заметим, что в определении общего решения иногда требуют, чтобы указанная алгебраическая система уравнений имела единственное решение 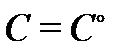 . Это требование будет, очевидно, всегда выполненным, если в области
. Это требование будет, очевидно, всегда выполненным, если в области 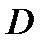 реализуются все условия теоремы Коши.
реализуются все условия теоремы Коши.
Пример 1. Показать, что вектор-функция
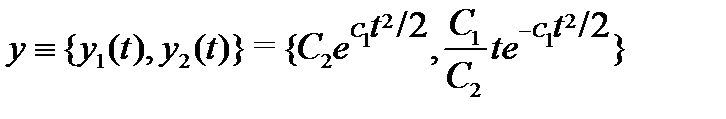
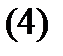
является общим решением системы
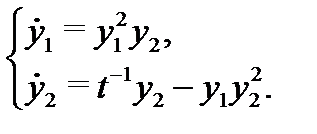
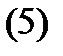
Решение. Вычислим производные от компонент вектор-функции (4):
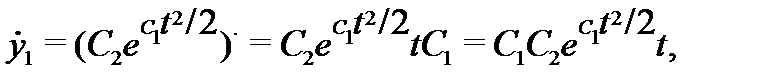
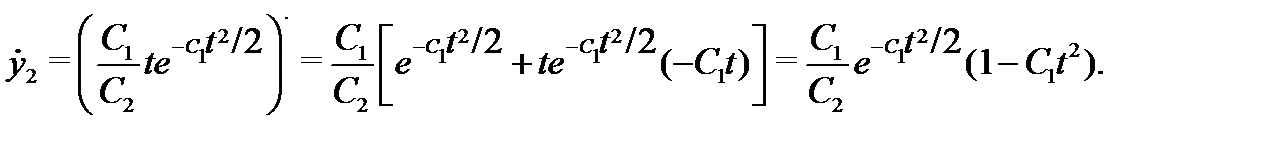
Вычислим правые части системы (5):
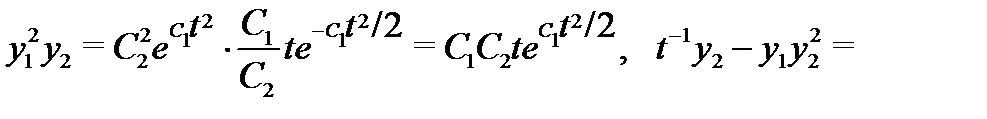
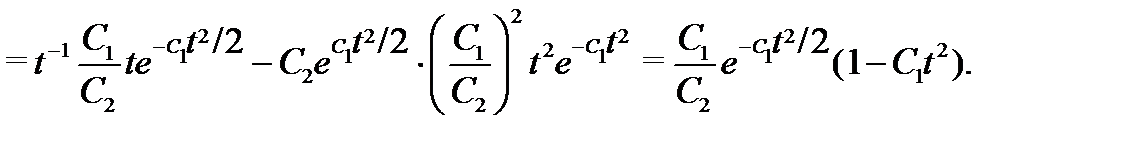
Сравнивая найденные значения производных с вычисленными правыми частями, видим, что при подстановке вектор-функции (4) в систему (5) получаются тождества. Это означает, что вектор-функция (4) является решением системы (5) на любом отрезке  не содержащим точку
не содержащим точку 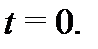
Рассмотрим теперь произвольную точку 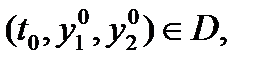 взятую из области
взятую из области 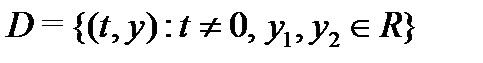 определения системы (5). Покажем, что алгебраическая система уравнений (3) имеет решение, В нашем случае (3) приобретает вид
определения системы (5). Покажем, что алгебраическая система уравнений (3) имеет решение, В нашем случае (3) приобретает вид
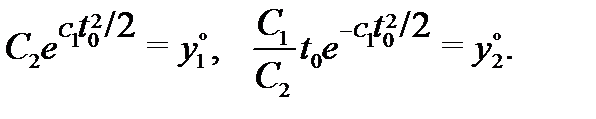
Умножая уравнения друг на друга, найдем, что
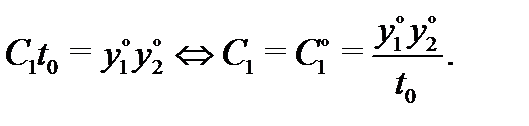
Подставляя это в первое уравнение, будем иметь
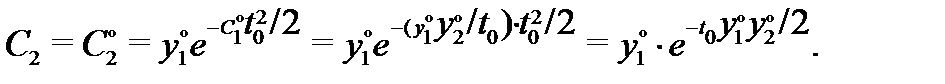
Таким образом, вектор-функция 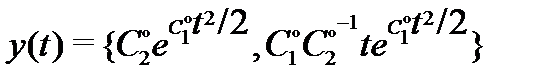 является решением системы (5) с начальным условием
является решением системы (5) с начальным условием 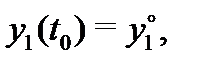
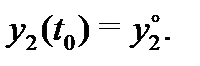 Это означает, что вектор-функция (24.4) является общим решением системы (5).
Это означает, что вектор-функция (24.4) является общим решением системы (5).
Общий и частный интегралы системы (1) определяются так же, как и в скалярном случае: это есть общее и частное решения системы (1), заданные соотношениями 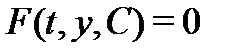 и
и 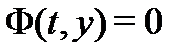 соответственно, из которых общее и частное решения определяются как функции, заданные неявно.
соответственно, из которых общее и частное решения определяются как функции, заданные неявно.
2. Методы интегрирования систем дифференциальных уравнений
Одним из методов решения систем дифференциальных уравнений является метод исключения, суть которого заключается в том, чтобы путем дифференцирования уравнений свести данную систему к одному дифференциальному уравнению высшего порядка. Рассмотрим этот метод на примерах.
Пример 2. Решить систему уравнений
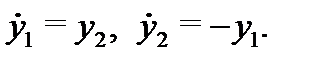
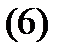
Решение. Дифференцируя первое уравнение системы (6) по 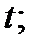 получаем уравнение
получаем уравнение 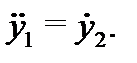 Производную
Производную 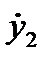 заменяем на
заменяем на 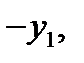 используя второе уравнение (6). В результате имеем уравнение
используя второе уравнение (6). В результате имеем уравнение
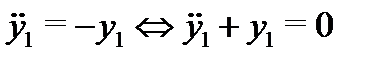
второго порядка относительно одной функции 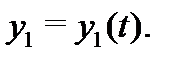 Его характеристическое уравнение
Его характеристическое уравнение 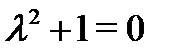 имеет два различных чисто мнимых корня
имеет два различных чисто мнимых корня 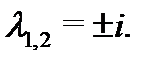 Значит, общее решение имеет вид
Значит, общее решение имеет вид 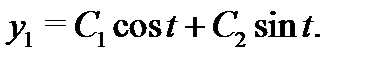 Поскольку
Поскольку 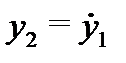 (см. первое уравнение (6)), то вторая компонента решения системы (24.6) вычисляется по формуле
(см. первое уравнение (6)), то вторая компонента решения системы (24.6) вычисляется по формуле 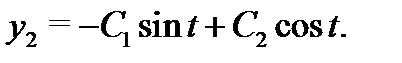 Таким образом,
Таким образом,
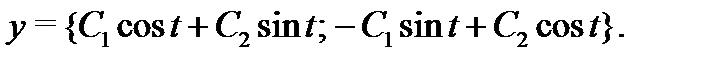
Пример 3. Решить систему уравнений
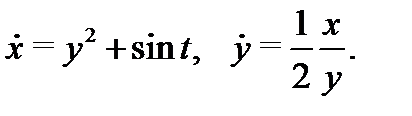
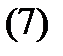
Решение. Дифференцируя первое уравнение системы (7), будем иметь 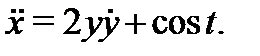 Из второго уравнения (7) находим
Из второго уравнения (7) находим 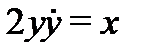 и подставляем в последнее уравнение. В результате будем иметь
и подставляем в последнее уравнение. В результате будем иметь
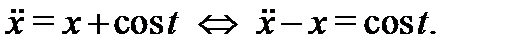
Это линейное уравнение второго порядка. Его общее решение вычисляем, например, методом подбора. Оно будет иметь вид
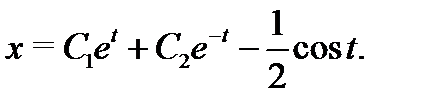
Из первого уравнения системы (7) находим
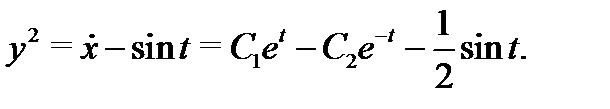
Следовательно,
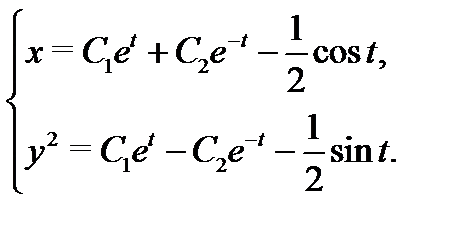
Заметим, что в последнем примере решение записано в виде интеграла.
Вторым способом решения систем уравнений является метод интегрируемых комбинаций. Суть этого метода состоит в том, чтобы подходящими преобразованиями привести исходную систему к одному дифференциальному уравнению относительно некоторой функции компонент данной системы. Если это уравнение легко интегрируется, то говорят, что оно является интегрируемой комбинацией данной системы. Получив достаточное число интегрируемых комбинаций, а затем рассмотрев их совместно, можно найти решение данной системы.
Пример 4. Решить систему уравнений
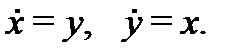
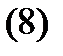
Решение. Эту систему можно было бы решить методом исключения. Однако попробуем найти ее решение методом интегрируемых комбинаций. Складывая почленно оба уравнения (8), получаем интегрируемую комбинацию
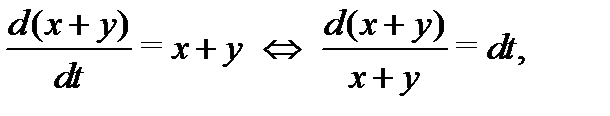
откуда вычисляем 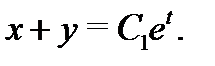 Вычитая из первого уравнения системы (8) ее второе уравнение, получаем еще одну интегрируемую комбинацию
Вычитая из первого уравнения системы (8) ее второе уравнение, получаем еще одну интегрируемую комбинацию
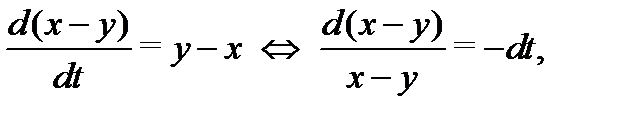
из которой находим 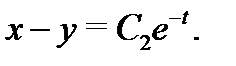 Итак, получено два алгебраических уравнения
Итак, получено два алгебраических уравнения
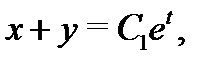
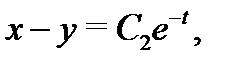
из которых легко находим решение системы (8):
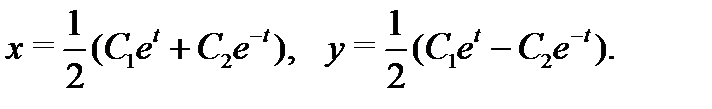
Соотношение 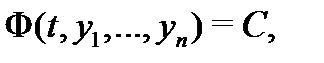 где
где 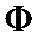 – скалярная функция,
– скалярная функция, 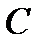 – постоянная, называется первым интегралом системы (1), если при подстановке в него решения
– постоянная, называется первым интегралом системы (1), если при подстановке в него решения  оно обращается в тождество. Часто первым интегралом системы (1) называют скалярную функцию
оно обращается в тождество. Часто первым интегралом системы (1) называют скалярную функцию  , сохраняющую постоянное значение на решениях
, сохраняющую постоянное значение на решениях  системы (1).
системы (1).
Ясно, что одна интегрируемая комбинация системы (1) позволяет выписать один первый интеграл этой системы. Если найдено 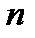 интегрируемых комбинаций, то получим
интегрируемых комбинаций, то получим 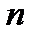 первых интегралов
первых интегралов
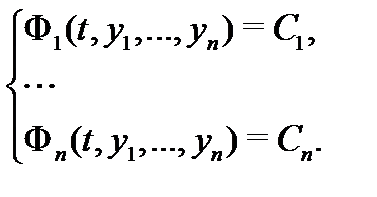
Если при этом определитель
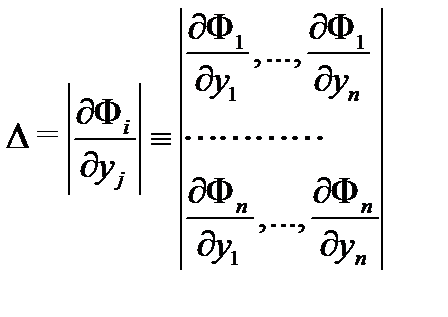
не равен нулю в области 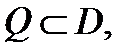 то (9) задают общий интеграл (в
то (9) задают общий интеграл (в 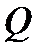 ) системы (1). Это означает, что система алгебраических уравнений (9) задает общее решение дифференциальной системы (1) в неявной форме. Заметим, что определитель
) системы (1). Это означает, что система алгебраических уравнений (9) задает общее решение дифференциальной системы (1) в неявной форме. Заметим, что определитель  называется якобианом системы функций
называется якобианом системы функций 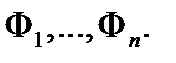 Если якобиан
Если якобиан 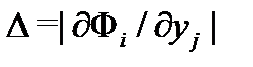 не равен нулю в области
не равен нулю в области 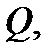 то система функций
то система функций 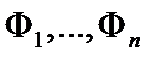 будет функционально независимой в
будет функционально независимой в 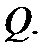 В этом случае система уравнений (9) может быть разрешена относительно
В этом случае система уравнений (9) может быть разрешена относительно 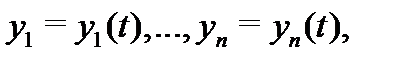 причем однозначно.
причем однозначно.
Дата добавления: 2016-06-05; просмотров: 2933;











