Свободные незатухающие колебания.
Отклонение x колебательной системы от положения равновесия при малых колебаниях удовлетворяет уравнению свободных гармонических колебаний
 ,
,
решением которого является гармоническая функция
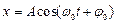 ,
,
где А – амплитуда колебаний;
φ0 – начальная фаза;
ω0 - циклическая частота колебаний.
Период колебаний Т – промежуток времени, в течение которого колебательная система совершает одно полное колебание, т.е. приходит в начальное состояние:
 ,
,
где N –полное число колебаний за промежуток времени Δt, ν – линейная частота.
Скорость v и ускорение a материальной точки, совершающей гармонические колебания (гармонического осциллятора):
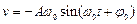 ,
,
Пружинный маятник – идеальная колебательная система, состоящая из тела, рассматриваемого в виде материальной точки, закрепленного на одном конце легкой пружины, другой конец которой неподвижен в некоторой инерциальной системе отсчета.
 .
.
Период колебаний пружинного маятника массы m с жёсткостью k, равен
 .
.
Математический маятник – идеальная колебательная система, состоящая из легкой нерастяжимой нити длины l, один конец которой фиксирован (точка подвеса), а на другом ее конце закреплено тело, рассматриваемое в виде материальной точки.
Период колебаний математического маятника равен
 .
.
Физический маятник – идеальная колебательная система в виде абсолютно твердого тела, насаженного на горизонтальную неподвижную ось, не проходящей через центр тяжести этого тела. (Рис. 2). Сила трения в оси подвеса (Oz,) тела отсутствует.
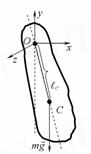
Рис.2.
Период колебаний физического маятника равен
 ,
,
где I – момент инерции маятника относительно оси, проходящей через точку подвеса маятника и перпендикулярной плоскости колебаний;
l – расстояние OC  от точки подвеса до центра масс маятника.
от точки подвеса до центра масс маятника.
Приведённая длина физического маятника:  . Используя приведенную длину, формуле периода колебаний физического маятника можно придать вид, аналогичный периоду математического маятника:
. Используя приведенную длину, формуле периода колебаний физического маятника можно придать вид, аналогичный периоду математического маятника:
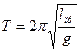 .
.
Кинетическая энергия гармонического осциллятора:
 .
.
Потенциальная энергия гармонического осциллятора:
 .
.
Полная энергия гармонического осциллятора:
 .
.
Средние значения кинетической и потенциальной энергий гармонического осциллятора:
 .
.
Результатом сложения гармонических колебаний, происходящих с одинаковой частотой в одном направлении, является также гармоническое колебание с амплитудой

и начальной фазой
 ,
,
где A1, A2, φ1, φ 2 – амплитуды и начальные фазы складывающихся колебаний.
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях
 ,
, 
имеет вид:
а) прямой  , если разность фаз
, если разность фаз  ;
;
б) прямой 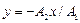 , если разность фаз
, если разность фаз  ;
;
в) эллипса  , если разность фаз
, если разность фаз  ;
;
г) окружности 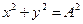 , если разность фаз
, если разность фаз  и амплитуды равны:
и амплитуды равны: 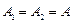 ;
;
Дата добавления: 2022-02-05; просмотров: 458;











