Основы термодинамики.
Число степеней свободы – это количество независимых переменных (координат), с помощью которых можно однозначно задать положение механической системы в пространстве. Число степеней свободы также равно числу независимых движений, которые может совершать механическая система. Для одноатомной молекулы газа число степеней свободы i=3, для двухатомной молекулы с жёсткой связью i=5, для многоатомного газа i=6.
Внутренняя энергия многоатомного газа U представляет собой суммарную кинетической энергии теплового движения всех ее молекул и их потенциальной энергии взаимодействия.
Средняя энергия теплового движения молекул

Внутренняя энергия многоатомного идеального газа равна
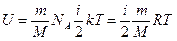
Внутренняя энергия макросистемы зависит только от термодинамического состояния этой системы. Внутренняя энергия является однозначной функцией состояния термодинамической системы и не зависит от способа перехода этой системы в данное состояние.
Количество теплоты Q (теплота)– энергия, переданная макросистеме путем теплообмена, т.е. в результате процесса передачи энергии от одного тела другому без совершения работы. Единица количества теплоты – джоуль (Дж).
Теплоёмкостью С системы называется величина, равная отношению сообщённого системе количества тепла δQ к изменению температуры системы dT
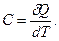
Удельная теплоёмкость с – теплоёмкость единицы массы вещества
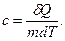
Молярная теплоёмкость С – теплоёмкость одного моля.
С=Мс
Зная удельную или молярную теплоёмкость системы, можно определить количество теплоты, полученной системой.
Элементарная работа δА сил давления газа при малом изменении dV его объема равна
δА=рdV
где p – давление газа.
Полную работу А, совершаемую газом при изменении его объёма от V1 до V2 , найдём с помощью интегрирования
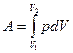
Графически работа определяется по площади заштрихованной фигуры (рис. 8)

Рис. 8.
Работа зависит от процессов, протекающих в газе.
- При изохорном процессе (V= const) А=0.
- При изобарном расширении (p= const) A = p(V2-V1).
- При изотермическом расширении (T= const)
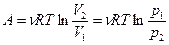 .
.
В основу термодинамики положены законы, являющиеся обобщением опытных фактов. Их называют начала термодинамики.
Первое начало термодинамики – закон сохранения энергии применительно к тепловым процессам. Количество теплоты Q, переданное макросистеме, идет на изменение ее внутренней энергии dU и на совершение работы A над внешними телами.
Математическое выражение I начала термодинамики в дифференциальной форме (для элементарного термодинамического процесса) имеет вид:
δQ= dU + δA.
Применение первого начала к изопроцессам.
- Изохорный процесс. Количество теплоты, переданное газу идёт только на приращение его внутренней энергии Q=ΔU= CvdT, где Cv - молярная теплоёмкость газа при постоянном объёме.
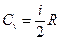 .
. - Изобарный процесс. Количество теплоты Q, переданное газу при изобарном процессе, идет на приращение внутренней энергии ΔU газа и на совершение работы A его силами давления:

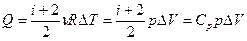 , где Сp – теплоёмкость при постоянном давлении.
, где Сp – теплоёмкость при постоянном давлении.  . Разность Сp-Cv=R называют уравнением Майера.
. Разность Сp-Cv=R называют уравнением Майера. - Изотермический процесс. Количество теплоты Q, переданное газу при изотермическом процессе, идет только на совершение работы A силами давления этого газа: A= Q .
- Адиабатический (адиабатный) процесс. Это - процесс, протекающий без обмена с окружающей средой. Уравнение адиабатного процесса (уравнение Пуассона):
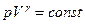
где 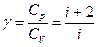 -адиабатическая постоянная или коэффициент Пуассона.
-адиабатическая постоянная или коэффициент Пуассона.
Адиабата (рис.9, кривая 2) на координатной плоскости pV идет круче изотермы ( кривая 1).
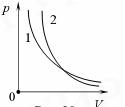
Рис. 9.
Первое начало термодинамики имеет вид: А = - ΔU, т.е. работа системы совершается за счёт уменьшения внутренней энергии.
Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние. На рV -диаграмме цикл (рис.10) изображается замкнутой кривой, где участок 1→2 соответствует расширению, а 2→1– сжатию газа.
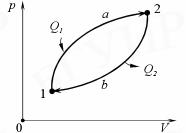
Рис. 10.
Тепловой двигатель (машина) – периодически действующее устройство, преобразующее теплоту в механическую работу. Любой тепловой двигатель
работает по круговому процессу (циклу).
Карно показал, что наиболее экономичным является двигатель, работающий по обратимому круговому циклу, состоящему из двух изотерм и двух адиабат (рис.11).
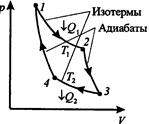
Рис. 11.
1→2 – газ изотермически (T1 =const ) расширяется, получая от нагревателя с температурой T1 количество тепла Q1,
2→3 – газ адиабатически расширяется, охлаждаясь до температуры Т2,
3→4 – газ изотермически (T2 =const) сжимается, отдавая холодильнику количество во теплоты Q2 ;
4→1 - газ адиабатически сжимается, при этом его температура увеличивается до Т2.
Теоремы Карно.
1.КПД цикла Карно с идеальным газом η зависит только от температуры нагревателя и температуры холодильника.
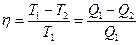
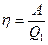
2.КПД любого теплового двигателя η1 не может превышать КПД теплового двигателя, работающего по циклу Карно в том же интервале температур:
η1 ≤η
КПД любого теплового двигателя можно также определить, как величину, равную отношению работы А, совершённой системой, к количеству тепла, полученному от нагревателя.

II начало термодинамики определяет направление процессов, происходящих в природе и связанных с превращением энергии
II начало термодинамики (формулировка Р. Клаузиуса, 1850 г.): невозможен процесс, единственным конечным результатом которого был бы переход теплоты от менее нагретого тела к телу более нагретому.
II начало термодинамики (формулировка У.Томсона (Кельвина), 1851 г.):
невозможны круговые процессы, единственным и конечным результатом кото-
рых было бы превращение всего полученного тепла целиком в работу.
Энтропия системы S. Это величина, которая является функцией состояния системы. Энтропия характеризует направление протекания самопроизвольных процессов в замкнутой термодинамической системе. Дифференциал этой величины 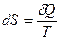 .
.
При переходе системы из состояния 1 в состояние 2
 .
.
В замкнутой системе для обратимых процессов  =0, для необратимых -
=0, для необратимых -  ›0.
›0.
Изменение энтропии в процессах идеального газа:
· Изохорный (V=const)  ;
;
· Изобарный (р=const) 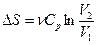 ;
;
· Изотермический (Т= const)  ;
;
· Адиабатический ΔS = 0.
Статистическое толкование энтропии. Число способов, которыми может быть реализовано данное термодинамическое состояние называется термодинамической вероятностью W. Как показал Больцман, энтропия пропорциональна натуральному логарифму W:
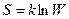 ,
,
где k- постоянная Больцмана.
Принцип возрастания энтропии. Любой необратимый процесс в замкнутой системе протекает так, что энтропия системы возрастает.
Третье начало термодинамики. Энтропия всех систем в состоянии равновесия стремится к нулю при приближении температуры системы к абсолютному нулю.

Это утверждение носит название теоремы Нернста-Планка.
Электростатика
Закон Кулона
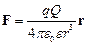
определяет силу F взаимодействия точечных зарядов q и Q;
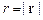 – расстояние между зарядами;
– расстояние между зарядами;
r – радиус-вектор, проведённый от заряда-источника Q к пробному заряду q, на который действует кулоновская сила;
ε0 – электрическая постоянная;
ε – относительная диэлектрическая проницаемость среды, в которой заряды взаимодействуют.
Напряжённость электрического поля, создаваемого точечным зарядом Q:
 .
.
Напряжённость и потенциал электрического поля, создаваемого системой N зарядов удовлетворяют принципу суперпозиции полей:
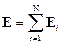 ,
, 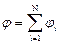 ,
,
где Ei, φi – напряжённость и потенциал электрического поля, создаваемого i-м зарядом в данной точке пространства.
Напряжённость и потенциал электрического поля, создаваемого заряженной до заряда Q проводящей сферой радиуса R на расстоянии r от центра шара:
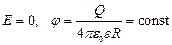 , при r < R;
, при r < R;
 , при r R.
, при r R.
Суммарный заряд, распределённый в объёме V, на поверхности S или на линии L:
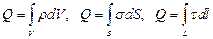 ,
,
где 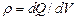 – объёмная плотность заряда;
– объёмная плотность заряда;
 – поверхностная плотность заряда;
– поверхностная плотность заряда;
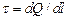 – линейная плотность заряда.
– линейная плотность заряда.
Связь потенциала с напряжённостью электрического поля:
а) 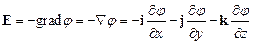 – в общем случае;
– в общем случае;
б) 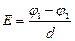 – в случае однородного поля;
– в случае однородного поля;
в) 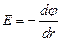 – в случае поля, обладающего центральной или осевой симметрией,
– в случае поля, обладающего центральной или осевой симметрией,
где  – векторный дифференциальный оператор “набла”;
– векторный дифференциальный оператор “набла”;
i, j, k – единичные векторы (орты) выбранной системы координат;
d – расстояние между двумя точками однородного поля с потенциалами φ1 и φ2, соответственно.
Разность потенциалов между двумя точками:
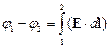
Напряжённость поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром радиуса R в точке, отстоящей от линии или оси цилиндра на расстояние r:
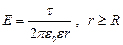 .
.
Напряжённость поля, создаваемого бесконечной равномерно заряженной плоскостью:
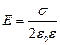 .
.
Электрический дипольный момент электрического диполя:
 ,
,
где l – плечо диполя (радиус-вектор, направленный от отрицательного заряда к положительному).
Потенциал и напряжённость поля диполя на больших расстояниях:
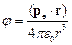 ,
, 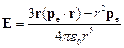 ,
,
где r – радиус-вектор, проведённый из точки наблюдения в середину диполя, 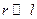 .
.
Работа кулоновских сил по перемещению заряда из точки с потенциалом φ1 в точку с потенциалом φ2:
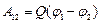 .
.
Потенциальная энергия взаимодействия системы N зарядов:
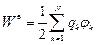 ,
,
где φ – потенциал поля в месте нахождения k-го заряда, созаваемого остальными зарядами.
Механический (вращательный) момент, действующий на электрический диполь, помещённый во внешнее поле E:
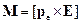 , или
, или 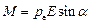 ,
,
где α – угол между векторами pe и E.
Потенциальная энергия электрического диполя во внешнем поле E:
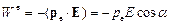 .
.
Индукция электрического поля, или электрическое смещение:
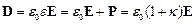 ,
,
где P – вектор поляризуемости среды;
κ– диэлектрическая восприимчивость среды.
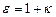 – относительная диэлектрическая проницаемость среды.
– относительная диэлектрическая проницаемость среды.
Условия на границе двух диэлектриков:
а) для тангенциальных составляющих напряжённости элек-трического поля:
 ;
;
б) для нормальных составляющих индукции электрического поля:
 ,
,
где σ– поверхностная плотность сторонних зарядов на границе раздела диэлектриков;
Электроёмкость уединённого заряженного проводника:
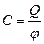 ,
,
где Q – заряд проводника;
φ – потенциал проводника.
Взаимная электроёмкость двух проводников:
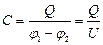 ,
,
где Q – заряд, который необходимо перенести с одного проводника на другой, чтобы изменить разность потенциалов между ними 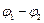 на 1 В.
на 1 В.
Электроёмкость уединённой проводящей сферы радиуса R:
 .
.
Электроёмкость плоского конденсатора:
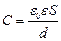 ,
,
где S – площадь одной пластины конденсатора;
d – расстояние между пластинами.
Напряжённость электрического поля внутри плоского конденсатора:
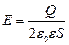 ,
,
где Q – заряд на обкладках конденсатора.
Энергия заряженного конденсатора:
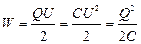 .
.
Дата добавления: 2022-02-05; просмотров: 570;











