Молекулярная физика.
Согласно основным положениям молекулярно-кинетической теории, все вещества состоят из атомов и молекул, находящихся в непрерывном хаотическом движении (тепловая форма движения материи), между которыми существуют силы взаимодействия (притяжения и отталкивания), зависящие от расстояния между ними.
Молекулярная физика и термодинамика – разделы физики, изучающие тепловую форму движения материи.
Макросистема – это система, состоящая из огромного числа частиц (молекул, атомов и др.). Совокупность огромного множества частиц, их движение и взаимодействие приводят к появлению у макросистем принципиально новых качеств и свойств, которыми не может обладать каждая частица в отдельности, характеризуемых такими физическими величинами, как температура, давление, удельный объем, коэффициент диффузии, теплопроводность, вязкость и др.
Микросостояние – это состояние макросистемы, которое задается указанием ее микропараметров – координат и импульсов (скоростей) каждой частицы этой системы.
Макросостояние – это состояние макросистемы, заданное значениями ее макропараметров (которые еще называют термодинамическими параметрами или параметрами состояния), которые в большинстве случаев можно непосредственно измерить приборами. К ним относятся температура, давление, объем, плотность, концентрация и др. Появление в огромной совокупности составляющих макросистему частиц качественно новых как свойств самой системы, так и закономерностей в поведении частиц обуславливает применение двух взаимно дополняющих методов
изучения макросистем – термодинамического и статистического.
Термодинамический метод – метод изучения макросистем на основе эмпирически полученных законов (начал), с помощью которого устанавливаются количественные соотношениях между макропараметрами этих систем без рассмотрения их внутреннего строения.
Статистический метод – метод изучения макросистем на основе их модельного представления как совокупности большого числа частиц и объяснения термодинамических закономерностей как результата их общего действия.
Термодинамический и статистический методы изучения макросистем дополняют друг друга. Термодинамический метод характеризуется своей общностью и позволяет изучать явления без модельных представлений об их внутренней структуре. Статистический же метод позволяет понять суть явлений, установить связь поведения и свойств макросистемы в целом с поведением и свойствами отдельных частиц. Их комбинированное применение способствует наиболее эффективному решению той или иной научной проблемы.
Термодинамическая система – совокупность рассматриваемых макросистем (макроскопических тел), которые могут обмениваться энергией и веществом как друг с другом, так и с внешней средой.
Термодинамические параметры (или параметры состояния) – физические величины, с помощью которых можно описать состояние макросистемы. Термодинамические параметры в большинстве случаев можно непосредственно измерить с помощью приборов. В качестве термодинамических параметров обычно выбирают температуру, давление и удельный объем.
Температура T – физическая величина, характеризующая состояние термодинамического равновесия макросистемы и являющаяся мерой интенсивности теплового движения молекул этой системы.
Термодинамическое равновесие (состояние равновесия) – состояние термодинамической системы, в которое она самопроизвольно переходит через некоторый промежуток времени, и которое характеризуется постоянством во времени термодинамических параметров. Температура – единственный термодинамический параметр, который одинаков для всех частей изолированной термодинамической системы, находящейся в состоянии термодинамического равновесия. Изменение значений термодинамических параметров макросистемы, находящейся в состоянии равновесия, возможно только при изменении внешних условий. Изолированной называется термодинамическая система, в которой отсутствует обмен энергией и веществом с внешней средой.
В СИ температура измеряется по абсолютной термодинамической шкале
(или шкале Кельвина), градуированной в кельвинах (К). Цена деления абсолютной шкалы и шкалы Цельсия одинакова. Температура T по шкале Кельвина и температура t по шкале Цельсия связаны равенством:
T =t + 273
В молекулярной физике принято характеризовать массу атомов и молекул не их абсолютным значением ( в килограммах), а относительной безразмерной величиной, называемой относительной атомной массой и относительной молекулярной массой. По международному соглашению в качестве единичной атомной массы принимается 1/12 массы изотопа углерода 12С : 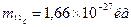
Относительная атомная масса A вещества – безразмерная физическая величина, равная отношению массы mа атома к единичной атомной массе.
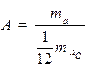
Относительные атомные массы химических элементов приведены в Периодической системе химических элементов Д. И. Менделеева.
Аналогично определяется относительная молекулярная масса M вещества
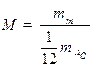
1 моль – это такое количество вещества, в котором содержится столько же частиц (атомов, молекул или других структурных единиц), сколько атомов содержится в 0,012 кг углерода. Моль любого вещества содержит одинаковое число атомов (молекул). Это число называется постоянной Авогадро Na= 6,02 ×1023 моль-1.
Если вещество содержит N атомов (молекул), то число молей 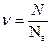 .
.
В молекулярной физике также пользуются понятием молярной массы М, которая определяется как масса 1 моль вещества М=mмолNa, где mмол – масса молекулы.
Идеальный газ – физическая модель, в которой:
1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда, в котором находится этот газ;
2) между молекулами газа отсутствует силовое взаимодействие на расстоянии;
3) столкновения молекул газа между собой и со стенками сосуда, в котором
они находятся, носят характер абсолютно упругих ударов.
Опыт показывает, что в состоянии термодинамического равновесия параметры состояния (объем V, давление p и температура T) макросистемы находятся в функциональной зависимости, которая называется уравнением состояния:
f (p, V, T)=0.
Для данного количества идеального газа ν, находящегося в состоянии термодинамического равновесия, уравнением состояния является уравнение Менделеева-Клапейрона, связывающее давление P газа, его объем V и температуру T:
PV = νRT,
где R= 8,31 Дж/(моль·К) – универсальная газовая постоянная.
Уравнение состояния идеального газа также можно записать в следую-
щем виде:
P=nkT
где n – концентрация молекул газа, T – абсолютная температура,
k – постоянная Больцмана. 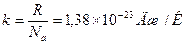 .
.
Всякое изменение состояния газа называется термодинамическим процессом.
Оытные законы идеального газа. Изотермический закон (закон Бойля-Мариотта):
для данного количества идеального газа при постоянной температуре произведение давления p газа на его объем V остается неизменным:
pV = const
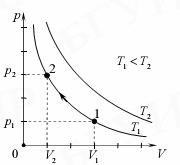
Рис. 4
Графически этот закон в координатах P,V изображается линией, называемой изотермой (рис. 4).
Изобарный закон (закон Гей-Люссака): для данного количества идеально-
го газа при постоянном давлении отношение объема V газа к его температуре T
остается неизменным:
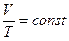
Графическая зависимость объёма от температуры изображается прямой линией –изобарой. (рис. 5 а). Зависимость в координатах P,V изображена на рис 5 б.
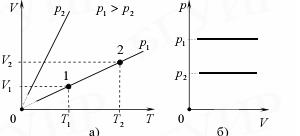

Рис. 3
Изохорный закон (закон Шарля): для данного количества идеального газа при постоянном объеме отношение давления p газа к его температуре T остается неизменным:
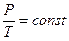
Графические зависимости представлены на рис 6.
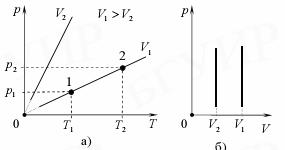
Рис. 6
Основное уравнение молекулярно-кинетической теории идеальных газов определяет давление газа через концентрации молекул n, массу отдельных молекул mо и среднюю квадратичную скорость их движения 
P= 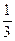 n mо< Vкв>2.
n mо< Vкв>2.
Можно получить другие выражения основного уравнения:
PV= 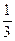 N mо< Vкв>2;
N mо< Vкв>2;
PV= 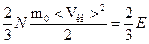 ,
,
где Е – суммарная кинетическая энергия всех молекул газа, N- общее число молекул, 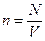 .
.
Скорости молекул газа имеют различные значения и направления, причем как величина, так и направление скорости каждой отдельной молекулы изменяются в результате соударений, поэтому нельзя определить число молекул, обладающих точно заданной скоростью в данный момент времени, но можно подсчитать число молекул, скорости которых лежат в интервале от v1 до v2.
Такая теоретическая зависимость была установлена Максвеллом на основании теории вероятностей:
dN(v) = 4π 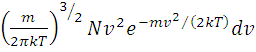
Функцию
f(v)= 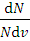 = 4π
= 4π 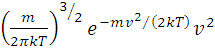
показывающую относительное число молекул, скорость которых лежит в интервале скоростей, называют функцией распределения молекул. В этой формуле: m - масса молекул, k – постоянная Больцмана, Т – абсолютная температура. Используя соотношение между постоянной Больцмана k и универсальной газовой постоянной R=kNA, формулу (2) можно переписать в виде:
f(v)= 4π 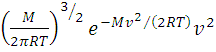
Графики функции распределения, соответствующие различным температурам, приведены на рис. 7.
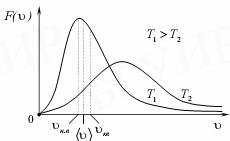
Рис 7.
Максимум кривой распределения соответствует наиболее вероятной скорости молекул vB, которую можно найти, исследовав на максимум функцию f(v).
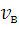 =
= 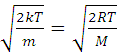 ,
,
Кроме наиболее вероятной скорости движение молекул газа характеризуют средняя арифметическая скорость 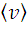 , определяемая формулой
, определяемая формулой 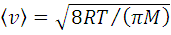 , и средняя квадратичная скорость
, и средняя квадратичная скорость
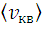 =
= 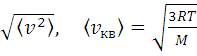 ,
,
равна корню квадратному из среднего арифметического значения квадратов скоростей. Если все молекулы одинаковы по массе, то vB< 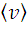 <
< 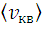 .
.
Дата добавления: 2022-02-05; просмотров: 768;











