Вынужденные колебания. Резонанс. Амплитуда и фаза вынужденных колебаний

Рассмотрим колебания, которые поддерживаются в системе внешней гармонической силой F = F₀Coswt. Такие колебания называются вынужденными.

Обратимся вновь к пружинному маятнику. Вспомним уравнения движения этого осциллятора:

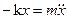— уравнение собственных незатухающих колебаний. В системе действует одна упругая сила F_упр = –kx;

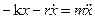— собственные затухающие колебания. В системе появилась сила вязкого сопротивления, пропорциональная скорости .

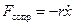В случае вынужденных колебаний кроме двух названных сил — упругой и силы сопротивления, на систему действует ещё одна сила: F = F₀Coswt.

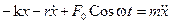— дифференциальное уравнение вынужденных колебаний пружинного маятника. Это уравнение движения принято записывать так:

.

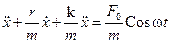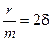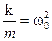Введя знакомые обозначения и , представим уравнение движения осциллятора окончательно в таком виде:

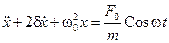. (13.14)

Опыт показывает, что под действием гармонического возмущающего усилия F = F₀Coswt осциллятор совершает гармонические колебания с частотой вынуждающей силы w:

х = ACos(wt + a). (13.15)

Если частота w известна, то задача сводится к определению амплитуды вынужденных колебаний А и начальной фазы a.

Продифференцировав функцию (13.15), подставим ее в уравнение (13.14):

.

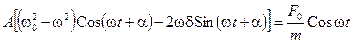Теперь воспользуемся известными тригонометрическими формулами для косинуса и синуса суммы двух углов:

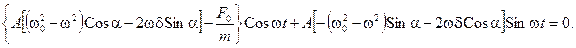
Это уравнение представляет собой сумму двух гармонических слагаемых

а Cos wt + b Sin wt = 0.

Последнее равенство возможно в единственном случае, если постоянные во времени a и b равны нулю: а = 0, b = 0. Это означает, что справедливы следующие уравнения:

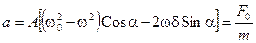, (13.16)

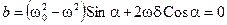. (13.17)

Эти два уравнения содержат только две неизвестные величины: амплитуду А и фазу a вынужденного колебания. Для отыскания амплитуды А можно домножить уравнение (13.16) на 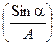, а уравнение (13.17) — на Cosa. Вычтя теперь из первого уравнения второе, получим Sina:

,

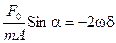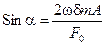. (13.18)

Воспользовавшись этим результатом в уравнении (13.17), найдем Cosa:

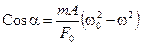. (13.19)

Возведем уравнения (13.18) и (13.19) в квадрат и сложим:

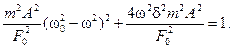
Последнее уравнение решим относительно искомой амплитуды колебаний А:

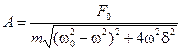. (13.20)

Фазовый сдвиг смещения x относительно возмущающего усилия F найдём непосредственно из уравнения (13.17):

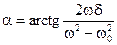. (13.21)

Обратимся к анализу полученных результатов.

1) Амплитуда вынужденных колебаний прямо пропорциональна амплитуде возмущающего усилия F₀.

2) Если w = 0 — случай приложения статической нагрузки F₀, смещение груза будет определяться жёсткостью пружины k:

.

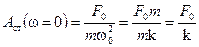3) При высоких частотах внешнего усилия (w→¥), амплитуда колебаний А→0.

4) Для отыскания частоты w_рез, при которой амплитуда достигает наибольшего значения А_рез, нужно найти минимум выражения, стоящего под корнем в знаменателе уравнения (13.20). Продифференцировав это выражение по w, и приравняв результат нулю, получим условие, определяющее w_рез:

.

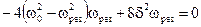Отсюда следует, что резонансная частота w_рез меньше частоты собственных незатухающих колебаний w₀:

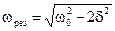. (13.22)

Используя это значение в (13.20), рассчитаем резонансную амплитуду:

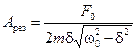. (13.23)

5) Если вязкое сопротивление отсутствует, коэффициент затухания d = 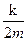= 0 и резонансная амплитуда устремляется в бесконечность. При этом условии резонансная частота, как следует из (13.22), равна частоте собственных незатухающих колебаний осциллятора w_рез = w₀.

6) С увеличением коэффициента затухания d, резонансная частота и амплитуда колебаний уменьшаются.

Все эти закономерности графически представлены на рис. 13.4.

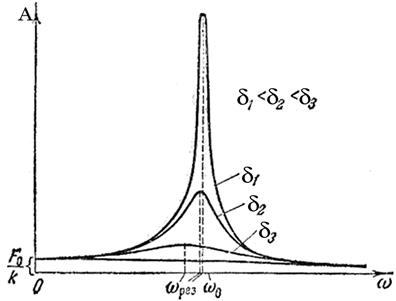
Рис. 13.4

7) При слабом затухании, когда 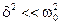, резонансная амплитуда равна

.

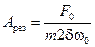Разделим это выражение на 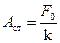— смещение под действием постоянной силы:

.

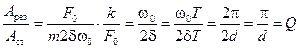Таким образом, добротность осциллятора численно равна отношению резонансной амплитуды к смещению под действием постоянной силы.

8) На рис. 13.5 представлена зависимость фазового сдвига вынужденных колебаний и вынуждающей силы — график функции (13.21). С увеличением частоты вынуждающего усилия a растет, меняясь от 0 до p. В резонансе фазовый сдвиг равен 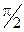. Эта зависимость a = a(w) меняется с изменением коэффициента затухания.

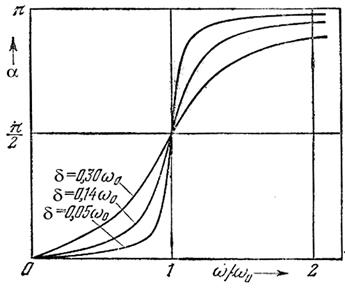
Рис. 13.5