Кинематика частицы и абсолютно твердого тела
Движение материальной точки по произвольной траектории на малом участке может рассматриваться как равномерное и прямолинейное. Мгновенная скорость v и мгновенное ускорение a материальной точки определяются как:
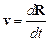 ,
, 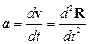 ,
,
где R – радиус-вектор материальной точки M в рассматриваемой системе координат.
Скорость v всегда направлена по касательной к траектории движения.
Величина средней скорости на малом участке:
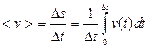 ,
,
где 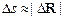 – путь, пройденный точкой за время Dt,
– путь, пройденный точкой за время Dt,
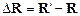 – перемещение радиус-вектора R за это же время.
– перемещение радиус-вектора R за это же время.
Величина среднего ускорения определяется аналогично:
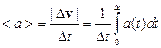 .
.
Если известна зависимость ускорения от времени, то скорость вычисляется по формуле
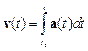 ,
,
а радиус-вектор материальной точки по аналогичной формуле
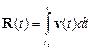 .
.
Полное ускорение при движении точки по произвольной траектории разлагается на сумму тангенциального ускорения at вдоль касательной к траектории в данной точке и нормального ускорения an, перпендикулярного этой касательной:
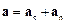 .
.
Движение материальной точки по окружности радиуса R характеризуется угловой скоростью w и угловым ускорением b:

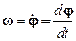 ,
, 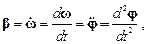
Если известна зависимость углового ускорения от времени, то угловая скорость вычисляется по формуле
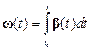 ,
,
а угол, на который повернётся материальная точка от начального положения, – по аналогичной формуле
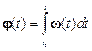 .
.
Угловая скорость указывает направление вращательного движения по окружности, соответствующее закручиванию правого винта. При движении по окружности связь между линейными и угловыми скоростями и ускорениями задаётся соотношениями
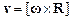 ;
; 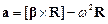 ,
,
где 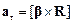 – тангенциальное ускорение,
– тангенциальное ускорение, 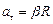 ;
;
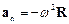 – нормальное ускорение,
– нормальное ускорение, 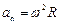 .
.
Величина полного ускорения:
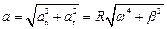 .
.
Углы jn между полным и нормальным ускорением и jt между полным и тангенциальным ускорением задаются соотношениями
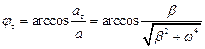 ;
;
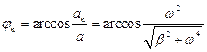 .
.
Движение абсолютно твёрдого тела представляется как сумма поступательного и вращательного движений. Поступательное движение может быть представлено движением любой точки тела. Чаще всего такой точкой является центр масс. При вращательном движении тела вокруг какой-либо оси все точки тела движутся по окружностям с одинаковыми угловыми скоростями и ускорениями. Основными формулами являются формулы, описывающие движение материальной точки.
Быстрота движения материальной точки по окружности или вращения тела вокруг оси характеризуется частотой вращения n – числом оборотов в единицу времени. Связь величины угловой скорости w с частотой вращения n задаётся соотношением
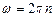
Период обращения:
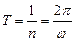 .
.
Динамика частицы.
Первый закон Ньютона (закон инерции): существует такая система отсчёта, относительно которой всякое тело, на которое не действуют другие тела, сохраняет состояние покоя или равномерного прямолинейного движения, пока действие со стороны других тел не изменит это состояние. Такая система называется инерциальной. Любая система отсчета, движущаяся равномерно и прямолинейно относительно заданной инерциальной системы отсчета, является инерциальной.
Принцип относительности Галилея: в любых инерциальных системах отсчёта все механические явления при одних и тех же условиях протекают одинаково, т.е. во всех инерциальных системах отсчета законы механики имеют одинаковую форму.
Из опыта известно, что в инерциальной системе отсчета изменение движения тела и (или) его деформация происходит в результате взаимодействия этого тела с другими телами.
Инертность тел. Свойство, присущее всем телам и заключающееся в том, что тела оказывают сопротивление изменению их скорости как по модулю, так и по направлению.
Масса тела. Масса m (инертная) – скалярная физическая величина, являющаяся количественной мерой инертности тела. В СИ [m] = 1 кг.
В ньютоновской механике считается, что:
- масса тела не зависит от состояния его движения (скорости);
- масса является аддитивной величиной, т. е. масса системы равна сумме масс всех тел, входящих в эту систему
Сила F – векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. В СИ [F]=1 Н.
Сила полностью определена, если заданы: ее модуль (величина), направление, а также точка приложения этой силы. Прямая, вдоль которой направлена сила, называется линией действия силы.
Второй закон Ньютона. Ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).
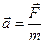 или
или 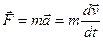 .
.
Импульс материальной точки. Векторная величина, численно равная произведению массы материальной точки на её скорость и имеющая направление скорости.
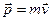 .
.
Используя понятие импульс, второй закон Ньютона можно сформулировать в более общем виде: изменение импульса материальной точки в единицу времени определяется результирующей силой, действующей на неё:
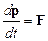 .
.
Если известна зависимость сил от времени, то изменение импульса за промежуток времени 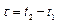 определяется по формуле
определяется по формуле
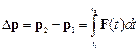 .
.
Система материальных точек движется как материальная точка с массой, в которой сосредоточена вся масса системы, положение которой определяет центр масс системы
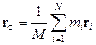 ,
,
где 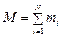 – масса системы.
– масса системы.
Импульс центра масс системы равен сумме импульсов всех материальных точек системы
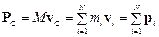 ,
,
Для замкнутой, или изолированной системы имеет место закон сохранения импульса
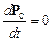 , или
, или 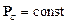 .
.
Силы, рассматриваемые в механике.
1) Силы тяготения ( гравитационного взаимодействия):
любые две частицы взаимодействуют вдоль соединяющей их прямой с силами притяжения, модуль каждой из которых прямо пропорционален произведению масс этих частиц и обратно пропорционален квадрату расстояния r между ними
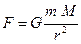
В векторном виде закон можно записать так:
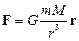 ,
,
где G – гравитационная постоянная
r – радиус-вектор, направленный от тела, на которое действует сила гравитации, к гравитирующему центру;
m и M – массы взаимодействующих тел.
На поверхности Земли сила гравитационного действия Земли на тело массы m определяет силу тяжести (без учёта вращения Земли)
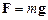
где g – ускорение свободного падения, определяемое по формуле
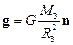 ,
,
где MЗ, RЗ – масса и радиус Земли
n – единичный вектор нормали к земной поверхности, направленный к центру Земли.
2) силы упругости, подчиняющиеся закону Гука
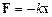 ,
,
где k – коэффициент упругости (в случае пружины – жёсткость);
x – абсолютная деформация одномерной упругой среды (удлинение или сжатие пружины или упругой нити).
Другая форма закона Гука
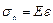
где 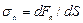 – нормальное напряжение при упругой продольной деформации тела;
– нормальное напряжение при упругой продольной деформации тела;
Fn – нормальная сила, действующая на поперечное сечение S тела;
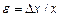 – относительное удлинение (сжатие) тела;
– относительное удлинение (сжатие) тела;
E – модуль Юнга.
3) силы трения, которые подразделяются на:
а) силы трения покоя: 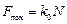 ,
,
где k0 – коэффициент трения покоя;
N – сила нормальной реакции;
б) силы трения скольжения: 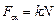 ,
,
где k – коэффициент трения скольжения;
N – сила нормальной реакции;
в) силы трения качения: 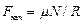 ,
,
где m – коэффициент трения качения;
N – сила нормальной реакции;
R – радиус качения;
г) вязкое, или жидкое трение – для малых относительных скоростей v слоёв жидкости или газа 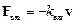 .
.
Работа и энергия
Энергия – скалярная физическая величина, являющаяся универсальной количественной мерой различных форм движения и взаимодействия материи. Механическая энергия W – энергия механического движения и взаимодействия. В системе СИ [W] = 1 Дж.
Изменение движения и (или) деформация тела в инерциальной системе отсчета происходит в результате силового взаимодействия этого тела с другими телами. При этом, как правило, происходит переход одного вида энергии в другой. Для характеристики процесса перехода энергии из одного вида в другой и его количественного описания вводится скалярная физическая величина – работа силы. Элементарная работа силы равна
dA = Fdr= F cosα ds =Fs ds ,
где α- угол между векторами F и dr, ds = |dr|- элементарный путь, Fs - проекция силы на вектор dr .
Работа силы по перемещению системы из положения 1 в положение 2 равна
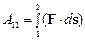 .
.
В поле консервативных сил эта работа равна
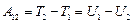 ,
,
где
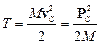
– кинетическая энергия;
U – потенциальная энергия системы, для которой справедливо соотношение
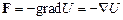 .
.
Для консервативных систем имеет место закон сохранения полной механической энергии
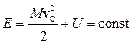 .
.
В поле неконсервативных сил эта работа равна
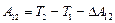 ,
,
где 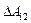 – работа, затраченная на преодоление внутренних сил сопротивления, равная работе сил сопротивления
– работа, затраченная на преодоление внутренних сил сопротивления, равная работе сил сопротивления 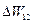 , взятой с обратным знаком:
, взятой с обратным знаком: 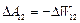 .
.
Работа сил сопротивления равна разности полных энергий в начальном и конечном состояниях
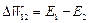 .
.
Дата добавления: 2022-02-05; просмотров: 447;











