Динамика твердого тела
Для характеристики внешнего действия на тело, приводящего к изменению его вращательного движения, вводится понятие момента силы.
Моментом силы относительно некоторой точки О называется векторная величина
M , равная векторному произведению радиуса-вектора r, проведенного из точки О в точку приложения силы F, и вектора этой силы:  . По модулю М=rFsinα. Вектор М всегда перпендикулярен плоскости, в которой лежат вектора r и F(Рис.1)
. По модулю М=rFsinα. Вектор М всегда перпендикулярен плоскости, в которой лежат вектора r и F(Рис.1)
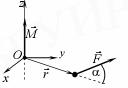
Рис.1
Моментом импульса частицы относительно некоторой точки О называется векторная величина L, равная векторному произведению радиуса-вектора r , проведенного из точки О в место нахождения этой частицы, и вектора ее импульсаp: L=[r×p].
Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки m на квадрат расстояния r от оси
J =mr2.
Момент инерции твердого тела относительно оси вращения равен сумме моментов инерции материальных точек, из которых состоит это тело. В общем случае, если тело сплошное и представляет собой совокупность точек с малыми массами dm момент инерции определяется интегрированием:
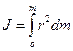 .
.
Основное уравнение динамики вращательного движения
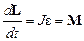 ,
,
где
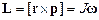
– момент импульса;
 – момент сил, действующих на тело, относительно начала координат;
– момент сил, действующих на тело, относительно начала координат;
r – радиус-вектор точки приложения силы;
w– угловая скорость вращения в плоскости векторов (r,p);
e– угловая скорость вращения в этой же плоскости;
J – момент инерции тела относительно оси вращения.
Собственные моменты инерции некоторых тел массы m:
1) тонкое кольцо, обруч, тонкостенный цилиндр радиуса R
а) относительно оси симметрии
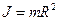 ;
;
б) относительно оси параллельной плоскости кольца, обруча
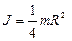 ;
;
2) тонкий диск, сплошной цилиндр радиуса R
а) относительно оси симметрии
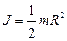 ;
;
б) относительно оси параллельной плоскости тонкого диска
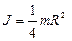 ;
;
3) сплошной шар радиуса R
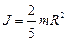 ;
;
4) тонкий стержень длины L относительно оси, проходящей через середину стержня перпендикулярно оси стержня
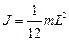 .
.
Закон сохранения момента импульса свободной системы тел, вращающихся вокруг неподвижной оси
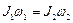 ,
,
где J1, J2 и w1, w2 – моменты инерции системы и угловые скорости вращения в моменты времени t1 и t2, соответственно.
Кинетическая энергия вращающегося тела
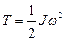 .
.
Дата добавления: 2022-02-05; просмотров: 424;











