Управление объектами с запаздыванием

4.7.1. Управление обычное и с прогнозом.Для возможности управления объект комплектуется приводом на входе и датчиком управляемой величины на выходе. Управляющий сигнал u(t) приводом и выходной сигнал датчика y(t) обычно рассматриваются как входной и выходной сигналы объекта управления. Промышленные объекты обладают значительной инерционностью, значительно большей, чем инерционность регулирующих и исполнительных устройств. Кроме того, в каналах передачи управляющих воздействий наблюдается явление транспортного (чистого) запаздывания. Поэтому в большинстве случаев динамика промышленных объектов может быть описана дробно–рациональной передаточной функцией с чистым запаздыванием.

Наличие запаздывания в контуре управления ведет к возрастанию фазового сдвига и тем самым сильно ограничивает полосу пропускания контура управления из-за опасности потери устойчивости. Большинству процедур синтеза управляющих устройств регулирования процессов с запаздыванием присуще использование прогнозирующего блока для компенсации запаздывания в контуре управления. В простейшем случае без использования прогнозирующих блоков задача может быть решена с помощью типовых регуляторов.

Ставится задача проектирования астатического контура управления с достаточно большим запасом устойчивости по фазе. Астатизм контура управления достигается за счет астатизма объекта управления или применением интегральных регуляторов для статических объектов. Запас устойчивости по фазе до 60 – 70 градусов достигается снижением коэффициента усиления и соответственно частоты среза разомкнутого контура. Чтобы при этом избежать потерь быстродействия, параметры регуляторов настраивают на максимальную компенсацию инерционности контура управления.

4.7.2. Регуляторы.Одноконтурная система управления обычно состоит из объекта управления и регулятора, образующих контур управления. Внешнее устройство задает желаемое y(t), от которого фактическое y(t) отличается на величину e(t) ошибки.

Регулятор предназначен для преобразования сигнала ошибки e(t) в управляющий объектом управления сигнал u(t) так, чтобы замкнутый контур работал бы максимально быстро, но с малым (< 5 %) перерегулированием. В зависимости от законов преобразования e(t) в u(t) регуляторы различают на две группы. К первой отнесем регуляторы, не содержащие интегральной составляющей: пропорциональные (П), пропорционально-дифференциальные (ПД). Ко второй отнесем регуляторы, содержащие интегральную составляющую: интегральные (И), пропорционально-интегральные (ПИ) и пропорционально-интегрально-дифференциальные (ПИД).

Корни полинома числителя передаточной функции называют нулями, корни полинома знаменателя передаточной функции называют полюсами. Полюсу соответствует излом вниз асимптотической ЛАХ на частоте равной модулю полюса. Нулю соответствует излом вверх асимптотической ЛАХ. Нулевое значение нуля соответствует операции идеального дифференцирования, нулевое значение полюса соответствует операции интегрирования.

Для регулирования без статической ошибки достаточно наличие нулевого полюса в передаточной функции разомкнутого контура управления. Принадлежит нулевой полюс объекту или регулятору не имеет значения. Поэтому для астатических объектов (с нулевым полюсом) применяют не астатические регуляторы ( П и ПД ). Для статических объектов применяют астатические регуляторы (И, ПИ и ПИД). Контура управления с астатизмом второго и более высокого порядка можно отнести к экзотике, хотя их реализация проблем не вызывает.

Регуляторы также разделяются по вносимым в контур управления нулям (изломами ЛАХ вверх). Число вносимых нулей на единицу меньше числа составляющих регулятора. Регуляторы ( П и И ) нулей не имеют, регуляторы ( ПД и ПИ ) имеют по одному нулю, ПИД-регулятор имеет два нуля.

4.7.3. Расчет параметров регуляторов обеспечивающий уменьшение суммарной инерционности контура управления.При настройке регуляторов их нули (изломы ЛАХ вверх) совмещают с полюсами (изломами ЛАХ вниз) объекта управления для компенсации последних. Чем больше полюсов объекта будет компенсировано, тем быстрее и эффективнее будет управление.

Теоретически можно компенсировать и положительные (неустойчивые) полюсы, практически – нельзя, так как при малейших изменениях параметров объекта или регулятора компенсация может нарушиться, и контур управления станет неустойчивым.

Не следует пытаться нулями регулятора компенсировать чистое запаздывание объекта управления. Фактически такие попытки всегда приводят к ускорению начала переходного процесса и затягиванию его окончания с увеличением его общей длительности.

Физическая реализация дифференциальных составляющих всегда сопровождается введением малой баластной инерционности Tb (большого по модулю полюса) в ПД и ПИД-регуляторы. Баластная инерционность Tb ограничивающей подъем усиления дифференциальной составляющей относительно пропорциональной составляющей величиной h.

Качество управления астатического контура достигается изменением общего коэффициента усиления и равной ему частоты среза wc до значения, обеспечивающего необходимый запас устойчивости по фазе. Чтобы вычислить желаемую wc, суммируем все инерционности Tsum контура: некомпенсируемые постоянные времени объекта, его чистое запаздывание, баластную инерционность, вносимую физической реализацией дифференциальной составляющей ПД или ПИД-регулятора.

В зависимости от величины желаемого перерегулирования:

[0 1 5 10 20] % выбираем число ke [0.35 0.4 0.5 0.6 0.75]. ke – эквивалентный, относительно суммарной инерционности, коэффициент усиления разомкнутого астатического контура. При ke < 1 наклон ЛАХ разомкнутого астатического контура на частоте среза равен –1 и желаемая частота среза wc этого контура вычисляется просто

wc = ke / Tsum.

Расчетная ЛАХ астатического контура управления с запаздыванием изображена на рис. 4.12. Остается изменить общий коэффициент регулятора для достижения желаемой wc.

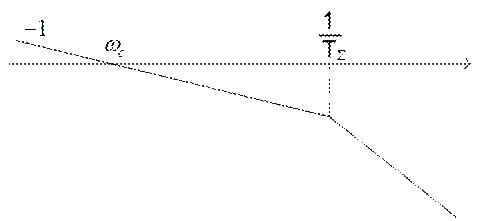
Рис. 4.12

Для получения микропроцессорного дискретного регулятора задаем допустимое ухудшение качества регулирования по сравнению с непрерывным регулированием в виде дополнительного перерегулирования и выбираем период дискретизации Ts относительно wc.

Если для преобразования непрерывного регулятора в дискретный, использовать билинейное преобразование Тастина, то выбору периода дискретизации Ts

Ts = kt / wc,

где kt = [0.1 0.15 0.25 0 .5 0.75 1], будет соответствовать дополнительное перерегулирование [2 3 5 10 15 20] %, к уже имеющемуся перерегулированию непрерывного контура.

Затем используем Матлаб для преобразование непрерывного регулятора (с именем reg) в дискретный (с именем regd)

regd = c2d (reg, Ts, ‘tustin’)

Дискретную передаточную функцию regd можно перевести в разностные уравнения regd2 в присоединенной канонической форме

regd2 = canon( ss(regd), ‘com’)

Эта команда выводит матрицы коэффициентов разностных уравнений дискретного регулятора. Вычисления по формулам

x(k) = a*x(k-1) + b*u(k),

y(k) = c*x(k) + d*u(k)

удобны для программирования.

4.7.4. ПИД-регулятор. ПИД-регулятор обычно используется для объектов статических, имеющих нулевой наклон ЛАХ на низких частотах на уровне Ko и изломы вниз на частотах [w1, w2, w3, w4,…]. Передаточная функция Wpid(p) ПИД-регулятора имеет вид

Wpid(s) = Kp + Ki / p + Kd*p / (Tb*p +1),

где Kp, Ki, Kd – коэффициенты закона управления для пропорциональной, интегральной и дифференциальной составляющим, Tb – баластная инерционность вычисления дифференциальной составляющей закона управления.

С помощью ПИД-регулятора можно трансформировать два полюса разомкнутого контура управления. Обычно трансформируют доминирующие полюсы, соответствующие изломам ЛАХ на низких частотах. Один полюс делают нулевым, т.е. излом ЛАХ на частоте w1 смещают влево на нулевую частоту, выбирая

Ki/Kp = w1.

Другой полюс увеличивают по модулю в несколько раз, т.е. смещая излом ЛАХ на частоте w2 вправо в h раз на частоту 1/Tb= w2*h выбором

Kp/Kd = w2.

Величина смещения h определяется возможностями реализации дифференциальной составляющей ПИД-регулятора, и не следует h увеличивать чрезмерно. С целью увеличения быстродействия управления частоту
1/Tb= w2*h желательно разместить сразу за частотой w3, так как дальнейшее смещение частоты не эффективно. Таким образом, ЛАХ разомкнутого контура с ПИД-регулятором имеет на низких частотах наклон – 1 с последующими несколькими изломами вниз [w3, 1/Td, w4,…].

Частота среза wc разомкнутого контура будет определяться интегральной составляющей регулятора и коэффициентом усиления объекта

wc = Ki*Ko.

Расчет сводится к следующему. Вычисляем суммарную некомпенсируемую инерционность

Tsum = 1/ (w2*h) + 1/w3 + 1/w4 + …

По выбранному ke вычисляем желаемую wc

wc = ke / Tsum.

После вычисления желаемой частоты среза wc последовательно вычисляем коэффициенты Ki интегральной, Kp пропорциональной и Kd дифференциальной составляющих ПИД-регулятора

Ki = wc / Ko;

Если частоты w1 и w2, компенсируемых изломов ЛАХ объекта далеко разнесены, можно воспользоваться приближенными формулами для вычисления пропорциональной и дифференциальной составляющих закона управления

Kp = Ki / w1; Kd = Kp / w2;

Точный расчет использует передаточнню функцию ПИД-регулятора, компенсирующая изломы ЛАХ объекта на частотах w1 и w2, имеющую вид

Wpid(p) = Ki*h/w1* (p + w1)*(p + w2) / (p*(p + w2*h)).

Именно в такой форме его и целесообразно реализовывать на микросхеме или микроконтроллере. В промышленных регуляторах часто выходной сигнал составляют из трех с раздельной регулировкой каждой составляющей. Если из Wpid(p) вычесть интеральную составляющую Ki/p, то получим передаточную функцию Wpd(p)

Wpd(p) = Wpid(p) – Ki/p

ПД-регулятора, коэффициент усиления которого равен Kp.

Если из Wpd(p) вычесть пропорциональную составляющую Kp, то получим передаточную функцию Wd(p)

Wd(p) = Wpd(p) – Kp

дифференциальной составляющих закона управления

Wd(s) = Kd*p / (Tb*p +1).

Записываем модель непрерывного регулятора, суммирую все составляющие

reg = Kp + tf(Ki, [1 0]) + tf([Kd 0],[Tb 1]).

4.7.5. Реализация ПИД-регулятора на операционном усилителе.Используется свойство операционного усилителя за счет большого коэффициента усиления и соответственно очень малого дифференциального напряжения входов, развязывать объединенные инвертирующим входом цепи, входную цепь и цепь обратной связи. Передаточная функция записывается как отношение операторных (комплексных) сопротивлений цепей, обратной связи и входной.

Операционные усилители обязательно балансируются по постоянному току включенным между неинвертирующим входом и землей резистором, проводимость которого равна суммарной проводимости всех цепей, соединенных с инвертирующим входом.

Схема c инвертированием сигнала ошибки достаточно проста и изображена на рис.4.13 .

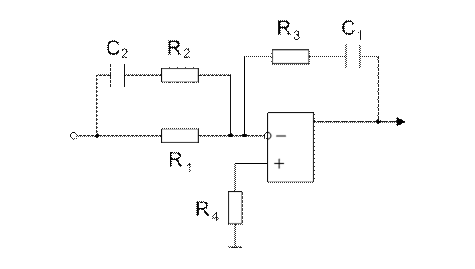
Рис.4.13 .

Сигнал ошибки подается на инвертирующий вход через резистор R1 и пераллельно ему включенной последовательной RC-цепи из резистора R2 и конденсатора C2. В обратной связи, между выходом и инвертирующим входом усилителя, последовательная RC-цепь из резистора R3 и конденсатора C1. Неинвертирующий вход усилителя соединен с землей резистором R4 = R1 для балансирования усилителя.

Интегральная составляющая Ki = 1/(R1*C1), пропорциональная Kp = R3/R1, дифференциальная Kd = ( R1+R2)*C2, баластная постоянная времени Tb = R2*C2. Изломы ЛАХ ПИД-регулятора вверх на частотах 1/(R3*C1) и 1/((R1+R2)*C2), излом вниз – на частоте 1/(R2*C2).

Схема совмещения на одном операционном усилителе сравнивающего устройства и ПИД-регулятора реализуется чуть сложнее и изображена на рис. 4.14.

Организуется второй вход схемы через резистор R4 = R1 на неинвертирующий вход усилителя. На этот вход подаем внешний сигнал управления, а на инвертирующий – сигнал от датчика обратной связи. Получаем Модифицированный ПИД-регулятор, у которого дифференциальная составляющая регулятора убрана из прямой цепи в цепь обратной связи. При этом передаточная функция разомкнутого контура сохраняется неизменной. Цель такой модификации – сделать управление более плавным, с меньшим ускорением и перерегулированием и, естественно, более медленным.

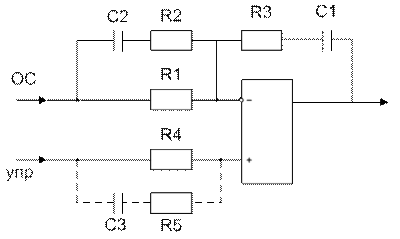
Рис. 4.14.

Для устранения вышеупомянутой модификации ПИД-регулятора параллельно R4 подключаем последовательную RC-цепочку R5 = R2 и C3 = C2. Получаем схему сравнивающего устройства и ПИД-регулятора на одном операционном усилителе.

Описанная схема трансформируется в ПИ-регулятор устранением RC-цепей R2-C2 и R5-C3. Для дальнейшей трансформации в И-регулятор необходимо еще и закорачивание резистора R3.

При расчете конденсаторов и резисторов следует учитывать, что если емкости конденсаторов задавать в микрофарадах, а сопротивления резисторов – в мегомах, параметры постоянных времени будут в секундах. Так как электролитические конденсаторы использовать невозможно из-за переменности знаков напряжений, используют керамические. Емкость монтируемого на печатной плате керамического конденсатора обычно не превышает 1 мкф. Резисторы не должны перегружать операционные усилители, и выбираются от 2 К до 10 М.

4.7.6. Микроконтроллерная реализация ПИД-регулятора.Для перехода к дискретному регулятору задаемся допустимым ухудшением качества управления (дополнительным перерегулированием), выбираем соответствующее kt и вычисляем Ts период дискретизации

Ts = kt / wc,

Затем используем преобразование непрерывного регулятора reg в дискретный regd

regd = c2d (reg, Ts, ‘tustin’)

Дискретную передаточную функцию regd можно перевести в разностные уравнения regd2 в присоединенной канонической форме

.

regd = canon( ss(regd), ‘com’)

Для наиболее сложного из регуляторов - ПИД-регулятора разностные уравнения имеют 2-й порядок, и для вычисления из сигнала ошибки e(k) управляющего сигнала u(k) требуют произвести на каждом такте управления 5 умножений и 4 сложения. Используя вычисленные командой canon матрицы ( a, b, c, d ) составляем алгоритм ПИД-регулятора, т.е. вычисления y(k) по u(k) и x(k-1) на k-м такте

x1(k) = a12*x2(k-1) + u(k), x2(k) = x1(k-1) + a22*x2(k-1),

y(k) = c11*x1(k) + c12*x2(k) + d11*u(k)

Здесь входной сигнал u(k) ПИД-регулятора – сигнал ошибки e(k), выходной сигнал y(k) – сигнал управления объектом.

4.7.7. И и ПИ-регуляторы.ПИ-регулятор имеет один нуль и может компенсировать лишь один полюс. Интегральный регулятор нулей не имеет и полюса компенсировать не может. Поэтому для одного и того же объекта управления суммарная некомпенсируемая инерционность Tsum для ПИ-регулятора будет больше, чем для ПИД-регулятора. И еще больше Tsum будет для И-регулятора. Соответственно будет уменьшаться желаемая частота среза wc контура управления и его быстродействие. Расчетные формулы коэффициентов регуляторов остаются прежними, только число коэффициентов и число составляющих закона регулирования уменьшается. Таким образом, регуляторы могут обеспечить приблизительно одинаковое качество управления, но при разном быстродействии. Чем больше составляющих в законе управления, тем выше быстродействие контура управления.

4.7.8. П и ПД-регуляторы.П иПД-регуляторы естественно применять для управления астатическими объектами. Пд-регулятор имеет один нуль и может компенсировать лишь один полюс. Пропорциональный регулятор нулей не имеет и полюса компенсировать не может. Поэтому для одного и того же объекта управления суммарная некомпенсируемая инерционность Tsum для П-регулятора будет больше, чем для ПД-регулятора. Вычисление желаемой частоты среза астатического контура производится по той же формуле, и для ПД-регулятора wc будет больше и быстродействии будет выше, чем для П-регулятора. В расчетных формулах коэффициентов регуляторов достаточно просто заменить имена

Kp = wc / Ko; Kd = Kp/ w1;

4.7.9. Управление с прогнозирующими блоками.Прогнозирующие блоки в принципе не могут устранить запаздывание из переходной характеристики объекта управления. Назначение их в устранении запаздывания из контура управления, чтобы сделать его переходные характеристики быстрыми с малым перерегулированием. Выходная величина объекта в системе с прогнозирующим блоком будет регулироваться с запаздыванием, но быстро и аккуратно.

Имеются различные способы прогноза для компенсации запаздываний по состояниям, выходам или управлениям. В основе всех их лежит одна и таже идея прогнозатора Смита, сочетания отрицательной обратной связи через модель объекта без запаздывания и положительной обратной связи через модель объекта c запаздыванием [1]. Схема системы управления объектом с запаздыванием с прогнозатором Смита изображена на рис. 4.15.

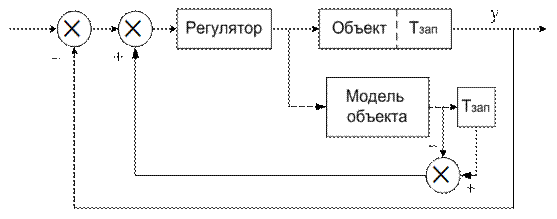
Рис. 4.15

Такие прогнозирующие блоки работают хорошо лишь при идеальном совпадении модели и объекта управления, когда положительная обратная связь модели точно компенсирует отрицательную обратную связь объекта. На практике этого достичь не удается, поэтому компенсация запаздывания в контуре управления не бывает полной. Учитывая это, при настройке регулятора контура управления с прогнозатором Смита соблюдают некоторую осторожность, не сильно форсируя процессы управления.

Очевидна необходимость решения задачи создания робастного прогнозирующего блока, пригодного для конструирования быстродействующих контуров управления в условиях неопределенности и изменяемости параметров объекта управления.

Очевидно, что совмещение столь противоречивых требований возможно лишь при выполнении некоторого количества постулатов:

1. Структура прогнозирующего блока не должна содержать положительных обратных связей.

2. Параметры прогнозирующего блока не должны увязываться с параметрами регулятора объекта.

3. Динамику процессов формирования прогнозирующего сигнала желательно развязать с динамикой процесса управления объектом.

4. Прогнозирующий блок должен иметь свой регулятор.

Вышеуказанным свойствам удовлетворяет структура полноразмерных наблюдателей. Чтобы создать прогнозирующий наблюдатель с вышеуказанными свойствами необходимо:

1. В модели наблюдаемого объекта все запаздывания трансформировать в запаздывания по выходу.

2. В качестве регулятора наблюдателя использовать интегральный регулятор. Это позволит получать высокую точность оценивания переменных вектора состояния модели объекта управления.

3. Параметры регулятора наблюдателя выбирать из условия сохранения устойчивости для наименее благоприятных значений изменяемых параметров объекта управления (коэффициента усиления, постоянных времени, величин запаздывания).

Таким образом, система управления состоит из контура управления объектом и контура управления наблюдателем. Схема системы управления с прогнгзирующим наблюдателем изображена на рис. 4.16.

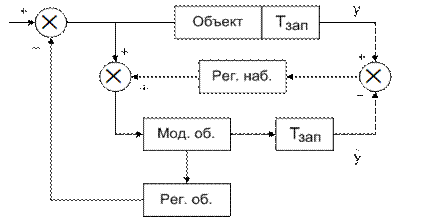
Рис. 4.16.

Модель объекта управления с запаздыванием является составной частью контура наблюдателя, быстродействие которого выбирается из условия устойчивости, т.е. ниже быстродействие основного контура управления. Регулятор основного контура рассчитывается для объекта без запаздывания, используя выходные сигналы наблюдателя, тем самым обеспечивает значительно большее быстродействие системы управления.

Отсутствие взаимозависимости динамики контура управления по управляющему воздействию и контура оценивания наблюдателя обеспечивается структурой наблюдателя.

4.7.10. Сравнение свойств прогнозирующего наблюдателя и прогнозатора Смита.Для исследования свойства робастности проводилось моделирование системы управления для трех вариантов модели объекта управления (номинальной, с завышенными и заниженными параметрами), которые отличались между собой дополнительными множителями (или делителями) для коэффициентов усиления, постоянных времени и величины запаздывания. Регулятор объекта для 3-х вариантов выбирался один и тот же, исходя из параметров модели номинального объекта без запаздывания. В частности регулятор обеспечивал переходные процессы без перерегулирования с длительностью в десятки раз меньше времени чистого запаздывания номинального объекта.

Выбор интегрального типа регулятора в контур наблюдателя обусловлен тем, что статический регулятор не устраняет полностью ошибку от параметрических возмущений объекта управления. В контуре регулятора наблюдателя присутствует запаздывание. Поэтому коэффициент усиления интегрального регулятора наблюдателя вычислялся для наименее благоприятного сочетания возможных изменений параметров объекта управления. Т.е. контур подстройки наблюдателя может быть чрезвычайно медлительным.

Моделирование показывает чрезвычайно высокую робастность прогнозирующего наблюдателя, не сравнимую с прогнозатором Смита. Прогнозирующий наблюдатель сохраняет устойчивость, форму и длительность переходных характеристик контура управления объектом при изменении параметров объекта в 10 и более раз. В то время как прогнозатор Смита работает при условии, что отличие объекта от его модели незначительное. Более того, система с прогнозирующим наблюдателем сохраняет работоспособность при таких изменениях объекта управления, при которых контур управления с объектом без запаздывания теряет устойчивость. Другими словами, прогнозирующий наблюдатель работает лучше адаптивного предсказателя Смита с идеальной самонастройкой.

Таким образом, переходный процесс управления с прогнозирующим наблюдателем состоит из трех частей: запаздывания, быстрого основного процесса управления, медленного процесса дотягивания из-за подстройки наблюдателя. Если параметры модели и объекта близки, процесс подстройки наблюдателя отсутствует.

4.8. Системы управления на базе модели объекта
в пространстве состояний

Совершенные системы управления проектируются с использованием модели объекта в пространстве состояний. Модальный или линейно-квадратичный регуляторы представляют собой набор безинерционных обратных связей по всем переменным вектора состояния модели объекта. Такой набор обратных связей по переменным вектора состояния позволяет полностью изменить характеристический полином объекта на любой желаемый. При расчете модального регулятора задаются все корни нового характеристического полинома. При расчете линейно-квадратичного регулятора задаются весовые коэффициенты минимизируемого интегрального критерия качества от квадратов переменных вектора состояния и управляющих переменных. Структурно регуляторы тождественны, но методики расчета совершенно разные. Обратные связи по виртуальным переменным модели естественно реализовать путем встраивания модели в закон управления в виде микроконтроллерной программы.