Точная и полная модель объекта управления. Микроконтроллерная система управления может и должна базироваться на достаточно точной и полной модели объекта управления.

Имеется объект управления с приводом, дополненный пропорциональным P регулятором, обеспечивающим желаемую динамику управления (частоту wo среза контура управления с жесткой ОС) без учета устойчивости и качества управления. Для простоты изложения пусть объект управления будет одномерным (Siso – один вход, один выход) и обозначим его как Ou.

4.8.2. Упрощенная модель объекта в пространстве состояний.Создается упрощенная (Ou_up) модель (порядка n) объекта в пространстве состояний, не содержащая изломов ЛАХ на частотах больше wo, если таковые имеются. Упрощения удобно производить в форме zpk, где видны частоты всех изломов. При отбрасывании излома вниз (вверх) коэффициент K формы zpk делится (умножается) на частоту излома.

4.8.3. Модальный регулятор объекта.Для упрощенной модели (с матрицами A, B, C, D)

[A, B, C, D]=ssdata(Ou_up)

вычисляется модальный регулятор объекта

u(t)=K*x(t),

где К – строка коэффициентов ОС по переменным x(t) вектора состояния.

Для этого необходимо выбрать эталон (содержащийся в функции pol) качества (‘a’, ‘b’, ‘k’, ‘l’, но не ‘o’), определяющий форму переходной характеристики, и задаться масштабирующим множителем mt для желаемых полюсов замкнутой системы. Для сохранения в модальном регуляторе эквивалента единичной обратной связи задаем масштабирующий множитель равным частоте среза объекта, т.е. mt = wo. Затем желаемые полюса po упрощенной модели объекта можно вычислить как корни полинома, умноженные на wo

po = roots (pol (n, ‘l’))*wo,

а модальный регулятор K объекта для их обеспечения вычисляется как

K=acker(A, B, po).

Формально модальный регулятор K замыкает объект положительной обратной связью, а фактический знак обратной связи содержится в знаке коэффициента. Чтобы свести к стандартной структуре с отрицательной обратной связью, заменяем регулятор на – K. Модальный регулятор K объекта встраивается в модель объекта в виде дополнительного выхода, т.е. строки в матрице С, т.е. [C; – K]. Здесь разделитель точка с запятой.

Модальный регулятор объекта для присоединенной строчной управляемой канонической формы.Для присоединенной строчной управляемой канонической формы

Ou_up1=canon(Ou_up,’com’) .’

Строка К вычисляется как разность коэффициентов фактического характеристического полинома и желаемого.

4.8.4. Наблюдатель для упрощенной модели.Реализация n обратных связей модального управления требует n датчиков или наблюдателя. Наблюдатель представляет собой модель объекта и собственный модальный регулятор по рассогласованию выходов объекта и модели. Проектируется наблюдатель для упрощенной модели объекта. Динамику наблюдателя относительно динамики объекта задаем множителем wn=[0.1, 1/3, 1, 3, 10] большим или меньшим единицы. Для задания полюсов pn наблюдателя можно использовать корни как другого, так и того же полинома. Тогда желаемые полюса наблюдателя

pn = po*wn.

Вычисляем модальный регулятор наблюдателя (L – столбец коэффициентов ОС от выхода к переменным вектора состояния)

L=acker(A’, C’, pn )’

Модальный регулятор L наблюдателя встраивается в модель объекта в виде дополнительного входа, т.е. столбца в матрице B, т.е. [B,L]. Здесь разделитель запятая.

Модальный регулятор наблюдателя для присоединенной столбцовой наблюдаемой канонической формы.Для присоединенной столбцовой наблюдаемой канонической формы

Ou_up2=canon(Ou_up,’com’)

Столбец L вычисляется как разность коэффициентов желаемого характеристического полинома и фактического.

4.8.5. Упрощенная модель с встроенными модальными регуляторами как основа микроконтроллерного управления.Упрощенную модель с двумя встроенными модальными регуляторами объекта (K) и наблюдателя (L) обозначаем Ou_up_KL

Ou_up_KL = ss ( A, [B,L], [C; – K], 0)

Здесь квадратными скобками обозначено объединение матриц: дополнительный столбец L присоединяется к матрице B через запятую, дополнительная строка K присоединяется к матрице C через точку с запятой. Подходящий размер нулевой матрицы D подбирается автоматически. Структурная схема модели в пространстве состояний с встроенными модальными регуляторами объекта и наблюдателя изображена на рис 4.17.

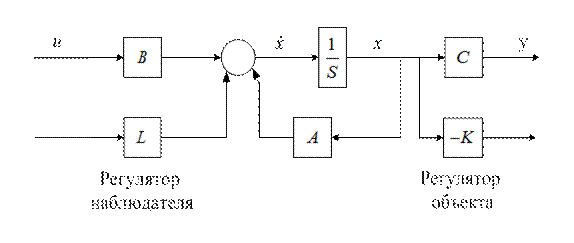
Рис 4.17.

4.8.6. Пропорционально-дифференциальный регулятор. Проектируем пропорционально-дифференциальный (PD) регулятор для компенсации различия объекта и его упрощенной модели. Суммируем отброшенные постоянные времени (To) объекта при переходе от точной модели Ou к упрощенной Ou_up. Знаменатель PD-регулятора делаем стандартным, с постоянной времени в 4 раза меньшей

PD = tf([To 1],[To / 4 1]).

Если PD-регулятор подключаем ко входу объекта управления, то его динамика форсируется и приближается к динамике упрощенной модели. Для реальных объектов такое форсирование динамики не всегда уместно и наталкивается на физические ограничения входного сигнала.

Если PD-регулятор подключаем к выходу объекта управления, между датчиком и наблюдателем, то управление объектом происходит более плавно, и его динамика не форсируется.

Инерционная часть PD-регулятора безусловно влияет не лучшим образом на процессы совмещения выходов модели и объекта. Инерционость PD-регулятора может быть совмещена с уже имеющеюся инерционностью модели. Для этого в модели необходимо организовать дополнительно к входу регулятора наблюдателя вход по его прозводной. И на этот вход подавать сигнал датчика с множителем То. Организовать вход по производной относительно другого входа возможно для любой модели, имеющей нулевую матрицу D. После чего матрица D обычно становится не нулевой, и организовать вход по второй и последующим производным удается лишь в редких случаях.

4.8.7. Шепинг фильтр для программного управления.Вход объекта управления (через PD регулятор) и вход модели подключаем к буферу (к=1), чтобы можно было ими управлять параллельно и одновременно одним сигналом. Схема управления объектом через шепинг фильтр изображена на рис. 4.18.

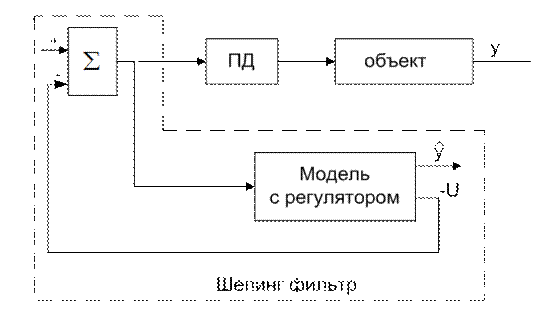
Рис. 4.18

При достаточно точной модели ПД-регулятор на входе объекта не требуется. На вход буфера заводим обратную связь от дополнительного выхода модели с регулятором – K. Из буфера и модели получаем шепинг фильтр shep

shep = connect (append (1, Ou_up_KL), [1 -3; 2 1], [1 3], [1 2]),

с двумя входами и двумя выходами. К одному выходу шепинг фильтра подключен через PD регулятор вход разомкнутого объекта. Таким образом выбранный эталонный закон управления реализуется на модели объекта и управляет параллельно включенным объектом, не используя никаких. сигналов датчиков. Такое управление разомкнутым объектом через шепинг фильтр может быть весьма эффективным при абсолютно точной модели и отсутствии возмущений объекта.

4.8.8. Управление в замкнутом контуре с наблюдателем.Из-за возмущений, в том числе параметрических, выходы объекта и модели будут расходиться. Чтобы притягивать выход модели к выходу объекта, организуем обратную связь по рассогласования выходов объекта и модели на дополнительный вход модели с регулятором L, т.е. создаем наблюдатель. Замкнутая система из объекта управления, наблюдателя и модального регулятора изображена на рис. 4.19. и образуется следующим образом

Ou_nab_reg = connect (append (Shep, Ou*PD), [3 1 0; 2 -2 3], 1, 3).

Если модель объекта не упрощалась на высоких частотах, то имеем классический модальный регулятор, встроенный в наблюдатель. Схема такого подключения изображена на рис. 4.19.

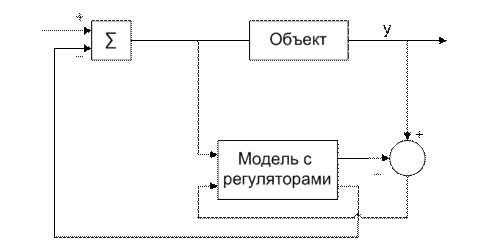
Рис. 4.19

В случае использования упрощенной модели, регулятор и наблюдатель будут квазимодальными. Т.е. спроектированными как модальные для упрощенной модели и снабженными средством компенсации упрощения, в данном случае PD- регулятором.

Для более плавного, без излишнего форсирования, управления PD-регулятор подключаем к выходу объекта управления, между датчиком и наблюдателем. Схема такого подключения изображена на рис. 4.20.

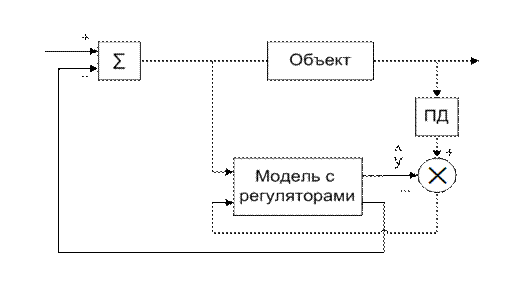
Рис. 4.20.

4.8.9. Микроконтроллерная реализация управления на базе модели.Для микроконтроллерной реализации важным является выбор периода дискретизации Ts и учета запаздывания tau на расчет алгоритма управления. Определяющими в расчетах являются частоты среза контуров управления и допустимые потери запасов устойчивости от дискретизации и запаздывания. Задача упрощается тем, что всех четыре регулятора (P, К, L, PD) и упрощенная модель реализованы целиком в одном микроконтроллере и лишь один контур наблюдателя замыкается через объект. Этот контур будет доминирующим при выборе Ts.

Быстродействие наблюдателя не влияет на длительность переходных процессов по управлению, поэтому его (через варьирование wn) можно уменьшать и тем самым увеличивать период дискретизации Ts.

Для разомкнутого контура объект – наблюдатель

Ou_nab_reg_r = Ou / P* nab_reg(1, 2)

можно вычислит запасы устойчивости и частоту среза wcn

margin (Ou_nab_reg_r),

и затем выбрать период дискретизации Ts

Ts = 0.7/ wcn.

Реализуемая в микроконтроллере управляющая часть, включающую все четыре регулятора, имет два входа и один выход. Обозначим ее как nab_reg

nab_reg = connect (append (Shep, P*PD), [3 1 ; 2 -2], [1 2], 3).

К выходу подключается объект управления. Первый вход – управляющий вход, ко второму – подключается датчик выходного сигнала объекта управления.

Алгоритм микроконтроллерной реализации динамического объекта с двумя входами естественен в виде разностных уравнений. Для получения алгоритма рекомендуется использовать преобразование Тастина

nab_reg_d = c2d ( nab_reg , Ts, ‘tustin’),

как наиболее точное и не дающее погрешностей в статике. Настраиваемое преобразование Тастина ‘prewarp’ уменьшает погрешности преобразования на определенной частоте wc, но может подвести на нулевой частоте, т.е. в статике, что обычно недопустимо.

4.8.10. Линейно-квадратичные регуляторы.В вышеизложенной методике вместо модальных могут быть использованы линейно-квадратичные регуляторы, совпадающие с модальными по размерности и способу включения в систему управления. Замена модальных регуляторов на линейно-квадратичные регуляторы сводится к замене способов вычисления матриц K и L.

Целесообразное вычисление линейно-квадратичного регулятора K объекта крайне затруднительно из-за отсутствия целенаправленных методик выбора коэффициентов целевой функции интегрального критерия качества, лежащего в основе всех расчетов. Т.е. использование линейно-квадратичного регулятора для регулирования объекта сомнительно.

Что касается использования линейно-квадратичного регулятора L в наблюдателе, то его расчет базируется на учете интенсивностей случайных возмущений объекта и интенсивностей шумов датчиков. Влияние первых надо максимально точно воспроизводить, а вторых – игнорировать. Т.е. расчет регулятора L наблюдателя ведется по реальным физическим условиям внешних воздействий, а не взятым с потолка желаемым коэффициентам, как при расчете регулятора K объекта. Поэтому линейно-квадратичный регулятор L в наблюдателе целесообразен, так как оптимизирует его по точности оценок вектора состояния и превращает в фильтр Калмана.

4.8.11. Введение нелинейностей в модель для предотвращения автоколебаний.Любому реальному объекту свойственны нелинейные свойства и нелинейные характеристики, по меньшей мере, характеристики насыщения. Попадание режима работы в зону нелинейностей может привести к автоколебаниям контура управления. Не приближение к зоне нелинейности гарантирует отсутствие автоколебаний. Для нелинейностей типа насыщение такое не приближение может быть достигнуто введением в модель нелинейностей с немного более сильными ограничениями, чем в объекте. Тогда будет происходить ограничение управляющего объектом сигнала в той мере, в какой это необходимо для не наступления нелинейных режимов работы объекта управления. При этом следует не допускать режима автоколебаний самой модели, что легко достигается достаточно простыми средствами внутри самой модели.