Синтез корректирующих обратных связей

Корректирующие обратные связи являются наиболее эффективными корректирующими средствами. По сравнению с последовательными они имеют существенные преимущества:

а) они уменьшают постоянные времени охваченных элементов и нелинейность их статических характеристик;

б) ослабляют влияние нестабильности параметров охваченных элементов на качество регулирования.

При глубокой обратной связи свойства части системы, охваченной обратной связью, определяются в основном свойствами цепи обратной связи, а не охваченных ею элементов. Поэтому обратными связями обычно охватываются наиболее инерционные, силовые элементы, а также элементы с нестабильными параметрами и нелинейными характеристиками.

Структурная схема системы с корректирующей обратной связью приведена на рис. 4.6.

Рис. 4.6

Передаточная функция скорректированной разомкнутой системы

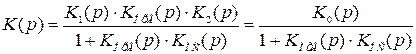, (4.40)

где 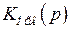– передаточная функция элементов системы, охваченных обратной связью;

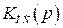– передаточная функция цепи обратной связи;

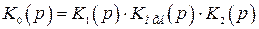– передаточная функция исходной системы.

При глубокой обратной связи, когда выполняется условие

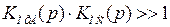, (4.41)

единицей в знаменателе выражения (4.40) можно пренебречь. Тогда передаточная функция скорректированной системы

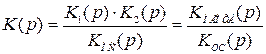(4.42)

не будет зависеть от охваченных ею элементов, а, следовательно, эти элементы не будут влиять на качество регулирования.

При коррекции обратными связями астатических систем, содержащих интеграторы, следует учитывать особенности действия обратной связи, связанные с возможностью снижения порядка астатизма. Для того чтобы порядок астатизма не изменился, необходимо, чтобы число дифференциаторов в цепи обратной связи было не меньше, чем число интеграторов в охваченной части. Если число дифференциаторов в обратной связи будет равно числу интеграторов в охваченной части, то при включении обратной связи коэффициент усиления уменьшится в 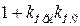раз. Для того чтобы коэффициент усиления не изменился, необходимо, чтобы число дифференциаторов в обратной связи было больше числа интеграторов в охваченной части.

4.6.1. Расчет местной корректирующей обратной связи.Расчет корректирующей обратной связи можно произвести путем пересчета эквивалентного последовательного корректирующего контура или непосредственно по ЛАХ. Системы будут эквивалентны, если их передаточные функции будут одинаковы

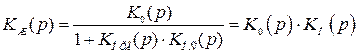, (4.43)

откуда

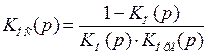. (4.44)

Выражение (4.44) позволяет найти передаточную функцию обратной связи, однако пользоваться им на практике оказывается сложно из–за сложности схемной реализации.

Согласно выражению (4.40) ЛАХ скорректированной системы

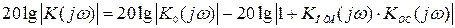. (4.45)

Для получения заданного качества регулирования она должна соответствовать желаемой:

.

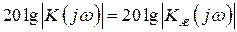Следовательно,

(4.46)

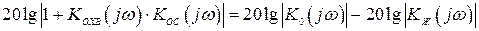
ЛАХ обратной связи легко определяется для интервала частот, где обратная связь глубокая. В этом случае, согласно выражению (4.42), получим

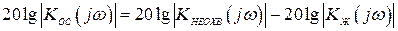
На частотах, где обратная связь не глубокая, где условие (4.41) не выполняется, необходимо по ЛАХ 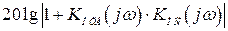определить ЛАХ 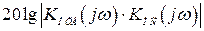. Для определения этой характеристики можно воспользоваться таблицами переходов, приведенными в [8], или же по виду ЛАХ записать выражение передаточной функции 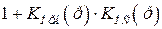и по нему найти аналитическое выражение передаточной функции .

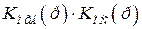Синтез параметров корректирующей обратной связи с использованием ЛАХ может быть осуществлен в такой последовательности:

1. Строится ЛАХ исходной системы 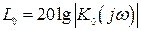, составленной из функционально необходимых элементов.

2. По заданным требованиям к качеству регулирования строится желаемая ЛАХ .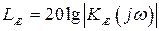

3. Вычитая 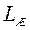из 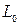, находят ЛАХ суммы

.

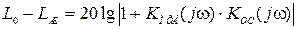4. По полученной ЛАХ строят характеристику

,

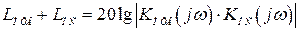для этого перехода необходимо изменить ЛАХ в области, близкой к нулю дБ, как показано пунктиром на рис. 4.7–4.10.

Следует отметить, что при расчетах методом ЛАХ желаемая ЛАХ 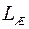не должна проходить выше 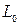, в противном случае ЛАХ суммы 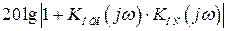будет отрицательной, т.е. 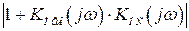будет меньше единицы, а произведение передаточных функций 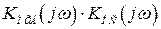будет отрицательным, что не позволяет пользоваться логарифмическими частотными характеристиками.

5. Строится ЛАХ охваченных элементов .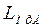

6. Вычитая 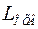из преобразованной ЛАХ 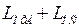, получают ЛАХ обратной связи.

7. По полученной ЛАХ записывают передаточную функцию обратной связи, выбирают схемную реализацию и рассчитывают ее элементы, проверяют согласование по входному и выходному сопротивлениям.

8. Проверяют устойчивость внутреннего замкнутого контура 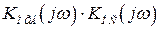на левой и правой частотах среза. Для нормальной работы скорректированной системы запасы устойчивости по фазе должны быть не менее 20 – 30 градусов.

4.6.2. Расчет глобальной корректирующей обратной связи.Вышеизложенная методика Бесекерского для расчета корректирующей местной обратной связи крайне запутана и применима для простейших случаев. Она предусматривает установку дополнительного датчика для организации местной обратной связи. На практике чаще приходится ползоваться лишь одним датчиком общей обратной связи, чаще всего цифровым. При этом корректирующая обратная связь получаеся глобальная, охватывающая все элементы прямой цепи.

В основу расчета положим свойство любой отрицательной обратной связи своей обратной частотной характеристикой отсекать частотную характеристику прямой цепи контура. Т.е. на график ЛАХ (усиления) прямой цепи накладываем график ослабления обратной связи. Точки пересечения графиков соответствуют усилению контура равному еденице, т.е. частоте среза контура. ЛАХ устойчивого замкнутого контура получается из ЛАХ прямой цепи отсечением ее части обратной связью. Контур будет иметь наклон ЛАХ – 1 или 1 и соответственно определенный запас устойчивости по фазе, если на частоте среза (точки пересечении графиков) наклоны графиков отличаются на единицу. Т.е. графики ЛАХ должны сходиться плавно. При разнице наклонов ЛАХ в 2 единицы устойчивости может и не быть, а при разнице в 3 и больше едениц гарантируется неустойчивость контура.

Система с корректирующей обратной связью имеет два контура управления. Для устойчивости обоих контуров (обратная) ЛАХ корректирующей обратной связи должна плавно пересекаться как с ЛАХ прямой цепи, так и с обратной ЛАХ главной обратной связи. Т.е. иметь наклоны – 1 и (–n + 1), если наклон ЛАХ прямой цепи равен – n в точке пересечения. ЛАХ объекта управления и обратные ЛАХ обратных связей изображены на рис. 4.11.

Рис. 4.11

Таким образом, глобальная корректирующая обратная связь всегда состоит из одного дифференцирующего звена и (n – 2)—х форсирующих звеньев.

Алгоритм расчета глобальной корректирующей обратной связи сводится к следующему:

1. Путем изменения коэффициента усиления (пропорционального регулятора) устанавливаем частоту среза разомкнутого контура с жесткой обратной связью равной желаемой частоте wo колебаний замкнутой системы.

2. Определяем число (n – 2) форсирующих звеньев корректирующей обратной связи по наклону (– n) ЛАХ на частоте > wo.

3. Выбораем частоту wf излома ЛАХ форсирующих звеньев чуть больше wo. wf = (1.1 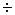1.3)*wo. Передаточная функция идеального форсирующего звена равна (p + wf)/wf.

4. Расчетываем желаемую частоту wc среза разомкнутого основного контура с замкнутым корректирующим контуром под желаемое перерегулирование (1 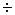5) % по формуле:

wc = (0.4 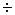0.5)*wf/(n – 2),

и соответстветствующей ей коэффициент усиления дифференцирующего звена с передаточной функцией p/wc.

5. Составляем корректирующую обратную связь как последовательное соединение из идеальных дифференцирующего и (n – 2)-х форсирующих звеньев.

6. Для придания корректирующей обратной связи свойства физической реализуемости, дополняем ее передаточную функцию (n – 1)-м апериодическим звеном с достаточно малой постоянной времени. Выбор постоянной времени желательно делать таким, чтобы в контуре корректирующей обратной связи запас по фазе был около 40 градусов.

Спроектированная таким образом система управления имеет обратную связь по (n – 1)-й производной, что дает ей чрезвычайно низкую чувствительность к изменению полюсов объекта, по модулю существенно меньших частоты среза корректирующего контура. Изменение знака полюса переводит объект в неустойчивый. При этом запас устойчивости по фазе внутреннего корректирующего контура уменьшается, но, как правило, контур не теряет устойчивости и переходные характеристики замкнутой системы практически не изменяются. Во многих случаях можно изменять знаки всех полюсов объекта без потери устойчивости системы управления.

Вышеизложенная методика расчета корректирующей обратной связи никак не использует параметры ЛАХ объекта на частотах ниже частоты среза, что подтверждает обоснованность упрощенной идентификации модели в виде последовательной цепочки из n интеграторов с передаточной функцией

Wo(p) = (wo/p)^n.

Возможно уточнение этой модели апериодическим звеном, учитывающим все малые постоянные времени объекта. Если влияние этого апериодического звена угрожает устойчивостивости корректирующего контура, можно ввести еще одно форсирующее звено в обратную связь. Параметр этого форсирующего звена может быть взят таким же, как и у остальных, или из условия компенсации малых постоянных времени объекта.

4.6.3. Пересчет глобальной корректирующей обратной связи в локальную обратную связь.Пересчет глобальной корректирующей обратной связи в локальную обратную связь основан на сохранении характеристик контура. Если локальная обратная связь не будет охватывать какие-то блоки прямой цепи, их передаточные функции следует добавить в обратную связь, чтобы сохранить свойства контура.

Замена двухконтурной системы управления одноконтурной системой. При цифровой реализации корректирующей обратной связи может быть произведена замена двухконтурной системы управления одноконтурной системой суммированием передаточных функций обратных связей. При этом сохраняются все свойства двухконтурной системы, в том числе ее низкая чувствительность к изменению параметров объекта.