Усилительно-преобразовательные устройства

Их назначение – обеспечить требуемый коэффициент усиления системы и согласовать элементы системы по виду и уровням сигналов. В состав усилительно–преобразовательных устройств можно отнести:

– предварительные усилители;

– модуляторы;

– демодуляторы;

– фильтры;

– аналогово-цифровые преобразователи;

– цифроаналоговые преобразователи;

– нелинейные преобразователи;

– логические устройства;

– устройства, выполняющие математические операции;

– динамические преобразователи (дифференциаторы, интеграторы);

и ряд других, которые необходимы для обработки информации в системах регулирования.

Почти все эти функции успешно реализуются микроконтроллерами, если хватает их быстродействия. Самые сложные законы управления естественно реализовать в виде программы микроконтроллера. Силовые ключи на выходе микроконтроллера позволяют создать управляющий сигнал любой мощности.

3.5. Технические средства для построения промышленных систем
регулирования

Для построения систем регулирования промышленными объектами в различных отраслях, таких как машиностроение, энергетика, нефтепереработка, химическая промышленность и других в настоящее время выпускается большое количество различных приборов и регуляторов, как в виде отдельных приборов, так и в виде агрегатированных комплексов. С помощью таких приборов и комплексов для конкретного технологического объекта путем набора необходимых приборов и блоков проектируются автоматические системы регулирования с требуемыми функциями, используя блочно–модульный принцип построения.

4. ИНЖЕНЕРНЫЕ МЕТОДЫ АНАЛИЗА И СИНТЕЗА
АВТОМАТИЧЕСКИХ СИСТЕМ

Анализ точности

При расчете и проектировании автоматических систем после выбора основных функциональных элементов и разработки структурной схемы системы перед разработчиком встает задача оценить, что получилось, т. е. провести анализ системы, составленной из функционально необходимых элементов, сопоставляя результаты с основными требованиями технического задания. К таким основным требованиям относятся: точность, устойчивость, динамические характеристики или качество работы в переходных режимах. Для решения этой задачи целесообразно использовать простые инженерные методы, позволяющие хотя и приближенно, но достаточно просто и быстро получить необходимые результаты.

Одним из основных показателей, характеризующих качество работы автоматической системы, является точность воспроизведения задающего воздействия. Точность обычно оценивают величиной ошибки в установившемся режиме работы. Она определяется несколькими факторами и может быть представлена в виде трех составляющих:

,

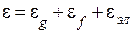где 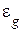– методическая ошибка, вызванная действием задающего сигнала;

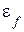– методическая ошибка, вызванная действием возмущений;

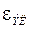– инструментальная ошибка, обусловленная погрешностями элементов системы.

Методические ошибки зависят от законов изменения задающего воздействия 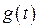и возмущения 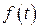, а также от структуры системы, порядка астатизма и параметров (коэффициента усиления, постоянных времени).

Инструментальная же ошибка определяется погрешностями изготовления элементов (люфт редуктора, дрейф нуля усилителя, неоднозначность характеристики датчика, зона нечувствительности исполнительного устройства). Ее можно изменять, только выбирая более точные и совершенные элементы. Для выбранных же элементов она изменяться не может и должна учитываться на этапе выбора элементов системы.

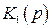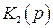Для оценки методических ошибок удобно воспользоваться структурной схемой и передаточными функциями по ошибке. В общем случае структурная схема автоматической системы может быть представлена в виде, изображенном на рис. 4.1, где и – передаточные функции элементов системы до точки приложения возмущения f и после нее, 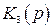– передаточная функция цепи передачи возмущения.

Передаточные функции по ошибке от входного сигнала и возмущения

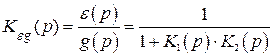, (4.1)

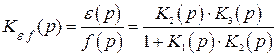. (4.2)

Изображение общей методической ошибки

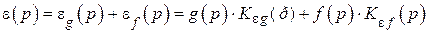. (4.3)

Зная передаточные функции по ошибке и законы изменения воздействий g(t) и f(t), можно найти выражение для ошибки:

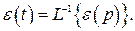
Установившееся значение ошибки может быть определено из выражения (4.3) по теореме о конечном:

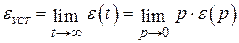. (4.4)

При отработке системой ступенчатых сигналов (скачок по положению, скачок скорости, скачок ускорения) или произвольных медленно меняющихся сигналов удобно пользоваться коэффициентами ошибок. Если передаточную функцию по ошибке представить в виде ряда по возрастающим степеням p, сходящегося при p→0

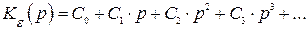, (4.5)

то коэффициенты этого ряда будут определять отдельные составляющие ошибки, обусловленные величиной сигнала, скоростью его изменения, ускорением и т.д., и называются коэффициентами ошибок по положению, по скорости, по ускорения и т.д.

Значения коэффициентов ошибок могут быть определены разными способами: разложением в ряд Маклорена, по методике Л. Г. Кинга, делением полиномов.

Так как передаточная функция по ошибке, записанная по коэффициентам ошибок, представляет ряд по возрастающим степеням p, то при вычислении коэффициентов ошибок путем деления полиномов последние также необходимо записывать по возрастающим степеням:

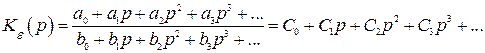, (4.6)

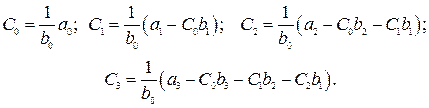(4.7)

При отработке гармонического сигнала 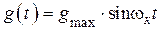ошибка не остается постоянной, а изменяется с частотой сигнала

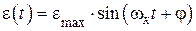. (4.8)

В этом случае точность системы оценивается по максимальной величине (амплитуде) ошибки. Для определения амплитуды ошибки можно воспользоваться частотной характеристикой по ошибке :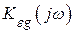

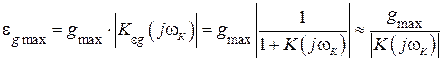. (4.9)

Для оценки точности следящих систем иногда пользуются величинами, обратными коэффициентам ошибок, которые называются добротностями по скорости, ускорению, моменту

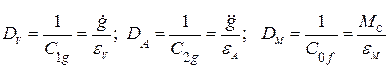, (4.10)

где 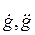– скорость и ускорение изменения сигнала;

– скоростная ошибка;

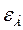– ошибка по ускорению;

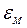– моментальная ошибка;

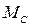– момент сопротивления нагрузки.

4.2. Синтез параметров автоматических систем из условия
обеспечения заданной точности

При расчете и проектировании автоматических систем разработчику важно знать, не как вычислить ошибку, а как определить параметры системы, которые бы обеспечивали требуемую точность.

Условие обеспечения заданной точности:

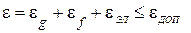. (4.11)

Так как инструментальная ошибка элементов системы определяется погрешностями самих элементов и корректироваться не может, то условие обеспечения заданной точности может быть записано в виде

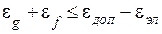, (4.12)

где 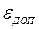– максимально допустимая величина ошибки;

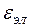– инструментальная ошибка элементов системы.

Требуемый порядок астатизма по задающему воздействию g(t) и возмущению f(t) определяется законами изменения сигналов. Постоянный по величине сигнал могут отработать как статические, так и астатические системы. Причем в астатических системах установившаяся ошибка будет равна нулю, а в статических определится коэффициентом усиления разомкнутой системы:

.

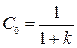Линейно нарастающий сигнал (скачок скорости) могут отработать только астатические системы, причем в системах с астатизмом первого порядка будет установившаяся ошибка, не равная нулю. Скачок ускорения могут отрабатывать системы с астатизмом не ниже второго порядка.

Для определения параметров автоматических систем по допустимой величине ошибки можно воспользоваться выражениями (4.1), (4.2), (4.3), из которых могут быть определены параметры передаточных функций по ошибке, обеспечивающие требуемую точность.

В общем случае эта задача не решается. Она может быть решена для конкретных систем. Рассмотрим это на примере электромеханической следящей системы, структурная схема которой изображена на рис. 4.2.

Рис.4.2

На структурной схеме угол поворота командной оси; 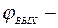угол поворота нагрузки; 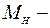момент нагрузки; 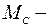момент нагрузки, приведенный к валу двигателя.

Эта структура сводится в виду, изображенному на рис. 4.1, где

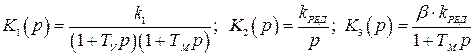. (4.13)

Запишем передаточные функции по ошибке

(4.14)

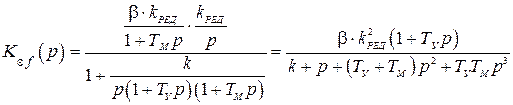. (4.15)

В этих выражениях k – коэффициент усиления разомкнутой системы.

Разложив передаточные функции по коэффициентам ошибок, получим:

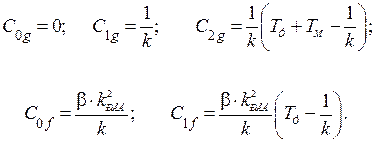(4.16)

Из этих выражений видим, что система обладает астатизмом первого порядка по задающему сигналу и является статической по возмущению (моменту нагрузки).

Условие обеспечения заданной точности 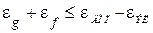позволяет рассчитать необходимый коэффициент усиления системы при отработке скачка скорости с постоянным моментом нагрузки:

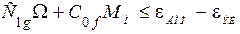, (4.17)

откуда

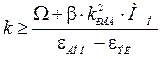. (4.18)

При работе на гармонический входной сигнал 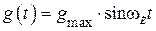максимальная ошибка по задающему сигналу определяется выражением (4.9).

В области низких частот 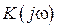описывается выражением:

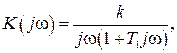
которому соответствует ЛАХ, изображенная на рисунке 4.3, где Т₁ – наибольшая постоянная времени системы.

Максимальная величина ошибки от задающего сигнала:

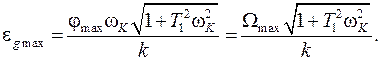(4.19)

Условие обеспечения заданной точности:

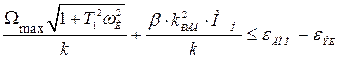, (4.20)

откуда

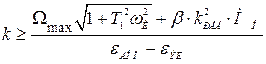(4.21)

Рис. 4.3

Из выражения (4.21) видно, что точность зависит не только от коэффициента усиления, но и от постоянной времени 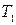. Для упрощения коррекции 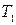желательно выбирать по возможности большей, но при этом возрастает величина требуемого коэффициента усиления. Уменьшение же 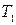сдвигает желаемую ЛАХ вправо, что усложняет коррекцию. Обычно выбирают

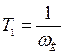, (4.22)

т.е. первую сопрягающую частоту делают равной частоте входного сигнала. В этом случаем произведение 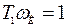, и условие обеспечения заданной точности упрощается:

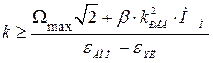. (4.23)

Этим выражением можно пользоваться при расчете на фиксированные перемещения ( 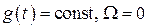) скачок скорости ( 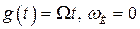) при отсутствии нагрузки ( 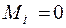). Для этого в выражениях (4.21) и (4.23) достаточно соответствующие величины положить равными нулю.

4.3. Анализ устойчивости и качества регулирования
в переходных режимах

Всякая автоматическая система должна обеспечивать заданную точность, быть устойчивой и обладать определенными динамическими свойствами, гарантирующими требуемое качество регулирования в переходных режимах. Устойчивость системы является необходимым условием ее работоспособности. Требования устойчивости и точности являются противоречивыми, поэтому устойчивость обычно оценивают после установления параметров, обеспечивающих заданную точность.

Устойчивость систем определяется корнями характеристического уравнения, описывающего свободное движение системы (при отсутствии внешних воздействий). Для устойчивости необходимо, чтобы корни лежали в левой полуплоскости на комплексной плоскости. Так как для уравнений выше третьего порядка вычислить корни сложно, то для анализа устойчивости пользуются критериями устойчивости, позволяющими определить, где находятся корни, не вычисляя их величины. Разработаны алгебраические критерии (Рауса, Гурвица), позволяющие оценить устойчивость по коэффициентам характеристического уравнения, и частотные критерии (Михайлова, Найквиста), позволяющие определить устойчивость по частотным характеристикам. В инженерной практике наибольшее применение находит критерий Найквиста с его интерпретацией на логарифмические амплитудную и фазовую частотные характеристики, так как, помимо устойчивости, он позволяет определить запасы устойчивости, т.е. насколько система далека от границы устойчивости.

Согласно критерию Найквиста система будет устойчива, если амплитудно–фазовая частотная характеристика разомкнутой системы не охватывает точку (–1, j0) на комплексной плоскости.

При оценке устойчивости по ЛАХ система будет устойчива, если при положительной ЛАХ ( 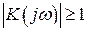) фазовая характеристика не пересекает ось 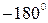или пересекает ее четное число раз.

Запасы устойчивости по модулю и фазе показывают, во сколько раз можно увеличить коэффициент усиления до выхода системы на границу устойчивости (запас по модулю) и на сколько градусов до 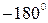не доходит фазовая характеристика при модуле, равном единице.

Качество регулирования в переходных режимах работы определяется по переходной характеристике и характеризуется следующими параметрами:

– временем переходного процесса ;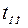

– установившейся ошибкой;

– периодом свободных колебаний 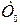или их частотой ;

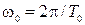– максимальным перерегулированием ;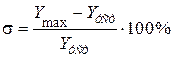

– числом колебаний за время переходного процесса;

– максимальной скоростью движения в переходном процессе и другими.

При расчете автоматических систем частотными методами для анализа устойчивости и качества регулирования удобно использовать показатель колебательности 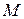. Он характеризует резонансные свойства системы и определяется отношением максимального значения АЧХ замкнутой системы 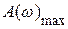к ее значению при :

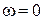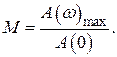
В астатических системах – А(0) = 1, а в статических – 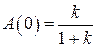и при больших 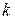, что необходимо для обеспечения точности, 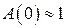. Поэтому показатель колебательности может быть определен как максимальное значение АЧХ замкнутой системы:

На основании теоретических исследований и большого числа экспериментальных данных рекомендуемое значение показателя колебательности находится в пределах от 1,3 до 1,5. При высоких требованиях к плавности регулирования в переходном процессе принимают меньшие значения: 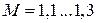, – и даже единицу. При 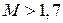переходный процесс будет сильно колебательным.

Для приближенной оценки качества регулирования удобно воспользоваться анализом ЛАХ и ФЧХ системы, которые достаточно просто строятся по передаточной функции разомкнутой системы. Типовая ЛАХ системы с астатизмом первого порядка изображена на рис. 4.4.

Рис. 4.4

Низкочастотная часть ЛАХ (НЧ) определяет установившийся режим работы (конец переходного процесса). Эта часть определяет порядок астатизма (наклон 0, –1, –2) и коэффициент усиления разомкнутой системы. При наклоне –1 выражение частотной характеристики – 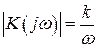, следовательно, величина коэффициента усиления будет равна частот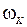е , где 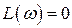, или на частоте 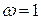ЛАХ будет проходить через точку .

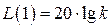Среднечастотная часть определяет устойчивость и основные показатели качества регулирования.

Базовая частота 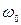(частота, где наклон –2 пересекает ось абсцисс) определяет добротность по ускорению (коэффициент ошибки по ускорению)

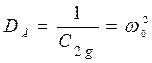. (4.24)

Частота среза 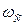и базовая частота 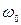определяют время переходного процесса

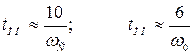. (4.25)

Величина максимального перерегулирования может быть оценена по запасу устойчивости по фазе. Для систем с типовыми ЛАХ

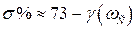, (4.26)

где 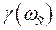– запас устойчивости по фазе.

Величина показателя колебательности М приближенно определяется длиной среднечастотного участка ЛАХ с наклоном –1:

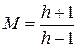. (4.28)

где величина 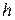определяется сопрягающими частотами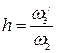

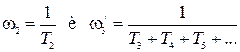. (4.29)

Начало среднечастотной части определяется постоянной времени 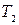, а ее конец 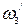– суммой малых постоянных времени.

Для замкнутой системы Wz с единичной обратной связью точнее значение показателя колебательности может быть вычеслено в Матлабе командой

M = norm(Wz, ‘inf’).

Аналитических зависимостей между параметрами переходной характеристики и показателем колебательности нет, но для систем с типовыми ЛАХ эти зависимости отражены в табл. 4.1.

Таблица 4.1

M	1,1	1,2	1,3	1,4	1,5	1,6	1,7
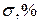
	13,8	20,3	26,5	32,2	37,5	40,7	44,6
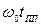
	7,75	6,3	5,85	5,6	5,45	6,1	7,25

4.4. Синтез параметров систем из условия обеспечения заданного
качества регулирования

При проектировании и расчете автоматических систем разработчику необходимо не только проанализировать, что получено, но и желательно определить, при каких параметрах системы будут обеспечены требуемые показатели качества. Иными словами требуется определить, как сделать систему, чтобы получить заданное качество работы.

В общем виде эта задача решения не имеет. Она может быть решена для частных случаев, когда передаточная функция системы и ее ЛАХ имеют типовую форму. Наиболее просто задача синтеза может быть решена с использованием типовых желаемых ЛАХ, т.е. таких ЛАХ, которые обеспечат получение заданных показателей качества.

В качестве желаемых ЛАХ при расчете автоматических систем наиболее часто используются типовые, приведенные в табл. 4.2.

Таблица 4.2

Вид ЛАХ	Передаточная функция

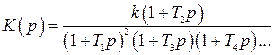
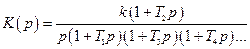
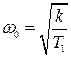
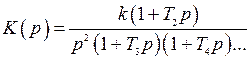
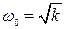
Для построения желаемых ЛАХ и расчета параметров передаточных функций могут использоваться методы В.В. Солодовникова и В.А. Бесекерского. В основу метода В.В. Солодовникова положена связь между качеством переходного процесса и параметрами вещественной частотной характеристики 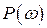. Он позволяет построить желаемую ЛАХ по заданному максимальному перерегулированию 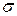и времени переходного процесса 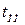при работе системы на ступенчатый сигнал (когда наибольшая постоянная времени 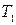не влияет на точность).

Метод В. А. Бесекерского позволяет рассчитать параметры желаемой ЛАХ по заданному показателю колебательности. Если помимо показателя колебательности заданы ограничения на время переходного процесса и максимальное перерегулирование, то, воспользовавшись табл. 4.1 (которая соответствует типовым ЛАХ), можно определить минимальные значения М,σ и ω₀, при которых будут удовлетворяться все заданные требования, и по ним рассчитать все параметры желаемой ЛАХ.

Следует отметить, что метод В.А. Бесекерского дает более точные результаты и позволяет осуществить коррекцию более простыми средствами. Параметры желаемой ЛАХ, рассчитанные по методике В.В. Солодовникова, оказываются завышенными. Среднечастотная часть желаемой ЛАХ с наклоном -1 удлиняется в сторону высоких частот. При этом усложняется коррекция системы.

Лучших результатов можно достичь при расчете параметров желаемой ЛАХ по методике В.А. Бесекерского. Последовательность расчета параметров и построение желаемой ЛАХ рассмотрим на примере электромеханической следящей системы.

Построение желаемой ЛАХ начинается с низкочастотной части, которая определяет установившийся режим работы. Параметры низкочастотной части – коэффициент передачи 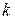и постоянная времени 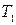(при работе на гармонический сигнал) – рассчитываются из условия обеспечения заданной точности. Методика их расчета рассмотрена в подразделе 4.2.

При расчете на ступенчатый сигнал 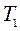может выбираться произвольно, так как ее величина не влияет на точность.

Если закон изменения входного сигнала точно не известен, а задана только максимальная скорость 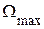и ускорение 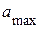, то расчет ведется на эквивалентный гармонический сигнал 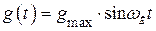, амплитуды скорости и ускорения которого равны заданным:

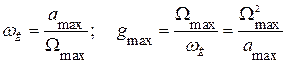. (4.30)

По вычисленному значению 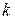проводится низкочастотная асимптота желаемой ЛАХ с наклоном -1 через точку 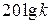на частоте 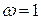или через точку 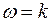на оси частот до первой сопрягающей частоты 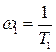, а затем – вторая асимптота под наклоном -2.

При расчете на гармонический входной сигнал (или эквивалентный гармонический) первая сопрягающая частота обычно выбирается равной частоте сигнала

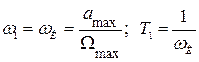. (4.31)

В точке пересечения второй асимптоты с осью частот (0 дБ) определяется базовая частота 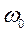, характеризующая добротность системы по ускорению:

.

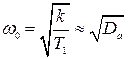В системах с астатизмом второго порядка первая асимптота проходит с наклоном –2 через точку с координатами 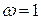, , 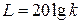а базовая частота 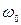в точке пересечения этой асимптоты с осью частот (0 дБ) численно равна .

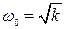По найденному значению базовой частоты 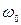и по заданному показателю колебательности М могут быть вычислены все постоянные времени желаемой ЛАХ, обеспечивающие заданное значение М:

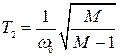; (4.32)

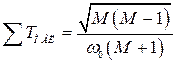, (4.33)

где 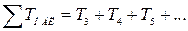– сумма малых постоянных времени, сопрягающие частоты которых больше частоты среза .

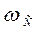В системах с астатизмом первого порядка допускается несколько увеличить 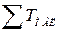, вычисляя ее по выражению:

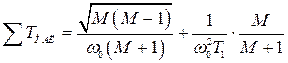. (4.34)

Если помимо показателя колебательности предъявляются требования по времени переходного процесса и максимальному перерегулированию, то для расчета постоянных времени может потребоваться корректировка значения 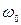, а при задании еще и допустимого значения перерегулирования – корректировка требуемого значения :

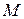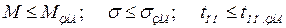. (4.35)

Для этого можно воспользоваться табл. 4.1. По заданным значениям 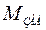и 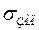выбирается расчетное значение показателя колебательности, удовлетворяющее условиям (4.35).

Рассчитывается значение базовой частоты 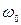, обеспечивающее требуемую точность (добротность по ускорению) и время переходного процесса:

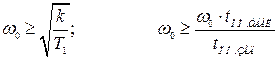, (4.36)

где 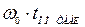– безразмерное время переходного процесса из табл. 4.2;

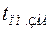– заданное время переходного процесса.

В дальнейшем при расчете постоянных времени принимается большее значение .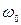

Число малых постоянных времени определяется порядком передаточной функции исходной системы. Для физической реализуемости корректирующих устройств наклон последней асимптоты желаемой ЛАХ должен быть таким же, как и у ЛАХ исходной системы. В области же частоты среза желаемая ЛАХ проходит под наклоном –1. Следовательно, число малых постоянных времени определяется последним наклоном ЛАХ исходной системы минус единица.

Улучшение качества регулирования. Следует отметить, что вышеизложенная методика и типовые ЛАХ не позволяют получать системы управления с показателем колебательности М = 1 и соответственно малое (< 5 %) перерегулирование переходных процессов. И причиной этого является наличие нулей в передаточной функции замкнутой системы. Чтобы не было нулей в передаточной функции, достаточно в желаемой ЛАХ устранить участок с наклоном – 2 в низкочастотной части. Конечно, это может сказаться на точности, но длительность переходной характеристики уменьшится приблизительно в 3 раза при одинаковой частоте среза. Если частоту среза взять в пределах 0.4 – 0.5 от частоты суммы малых постоянных времени, то гарантируется перерегулирование от 1 до 5 %, запас по фазе между 70 и 60 градусами и показатель колебательности М = 1. При этом можно будет обойтись более простым корректирующим устройством.

Для получения минимальной длительности переходных характеристик необходимо ограничить перерегулирование пятью процентами и минимизировать запаздывание и суммарную инерционность нескомпенсированных постоянных времени контура управления. Корректирующее устройство компенсирует большие постоянные времени объекта и вносит меньшие свои.

Если в требованиях по точности доминируют ошибки от возмущений, то имеет смысл рассмотреть задачу их компенсации отдельно от задачи управления. При этом, скорее всего не понадобится задирать вверх коэффициент усиления и полосу пропускания системы.