Методика аналитического определения математической модели

Аналитический метод базируется на использовании физических законов, определяющих ход процессов, происходящих в объекте.

Для простых объектов, в которых протекает один элементарный процесс, математической моделью будет запись уравнения, описывающего этот процесс. Решение задачи определения математической модели сложного объекта, в котором протекают различные физические процессы, может быть осуществлено в такой последовательности:

1. Выделяется объект из окружающей среды и изучается его физическая сущность и протекающие в нем процессы.

2. Определяется назначение объекта, и формулируются цели и задачи управления.

3. Определяются переменные (координаты) характеризующее качество работы (выходные, регулируемые переменные).

4. Устанавливаются переменные (координаты) изменение которых наиболее существенно влияет на качество работы объекта (возможные управляющие воздействия и возмущения).

5. Выявляются и формулируются зависимости между выходными координатами и критериями качества, а также между выходными координатами и возможными управляющими воздействиями и возмущениями, т.е. производится собственно математическое описание работы объекта.

При этом сложный объект удобно представить в виде совокупности более простых, элементарных составных частей с описанием связей между ними.

Декомпозиция объекта может осуществляться как по составу устройств и элементов, входящих в объект, так и по физической сущности процессов, происходящих в нем.

На основании анализа процессов, происходящих в отдельных элементах, структуры объекта определяются их математические модели, которые являются записью физических законов, которым подчиняются происходящие в них процессы. При этом необходимо учитывать связи между элементами структуры и обеспечивать их согласование по физической природе сигналов и их размерностям.

6. Определяется номенклатура и параметры управляющих воздействий, и накладываемые на них ограничения, а также возмущения.

7. По полученной структуре и математическим моделям элементов, путем исключения промежуточных переменных, определяются зависимости между выходными переменными, управляющими сигналами и возмущениями. Эти зависимости и являются собственно математической моделью объекта

8. Вычисляются численные значения параметров модели.

9. Оцениваются точность модели и ее адекватность реальному объекту.

Динамическая модель обычно создается с целью моделирования процессов управления. Поэтому ее совпадение с реальным объектом желательно: для частотных характеристик – вблизи частоты среза будущего контура управления, для переходных характеристик – в течение длительности переходной характеристики будущего контура управления. Несовпадение начала и окончания переходных характеристик модели и объекта (частотных характеристик на очень высоких и очень низких частотах) не являются дефектом модели при ее целевом использовании при проектировании системы управления. Еще одной причиной расхождения начала процессов являются нулевые начальные условия модели, в то время как у реального процесса бывает затруднительно создать установившейся режим без возмущений.

Как это ни покажется странным, но математическая модель динамики объекта будет зависеть от типа предполагаемого для управления регулятора. Если предполагается регулятор в обратной связи, обычно отсекающий ЛАХ объекта в низкочастотной и среднечастотной части, то отсекаемые части могут воспроизводиться более чем приближенно. Достаточно точно воспроизвести ЛАХ объекта на частотах больше его частоты среза и как-то учесть инерционности на высоких частотах. Поэтому весьма разумная модель объекта управления будет состоять из цепочки интеграторов с коэффициентом, обеспечивающим совпадение частоты среза, и одной инерционности как суммы малых постоянных времени. Совпадение модели и объекта будет на разгонной части переходной характеристики, по которой и определяют параметры модели при идентификации.

Методику аналитического определения математической модели проиллюстрируем на конкретных объектах, процессы в которых наглядны и достаточно хорошо изучены.

2.2.1. Одномассовые и многомассовые модели электромеханических систем.Электромеханические системы содержат электрический привод (электродвигатель) и механическую часть. Механическая часть чаще всего кинематически жеско связана с приводом и образует одну общую инерционную массу. Модель движения таких систем сводится к модели электропривода с увеличенной инерционной массой.

В случае сложной механической части с несколькими подвижными частями или упругой связью с электроприводом, модель движения усложняется до многомассовой, и требуется запись закона Ньютона для каждой массы с учетом их механического взаимодействия.

2.2.2. Математическая модель электродвигателя постоянного тока. Такие двигатели являются наиболее распространенными исполнительными устройствами в автоматических системах. Схема двигателя изображена на рис. 2.1.

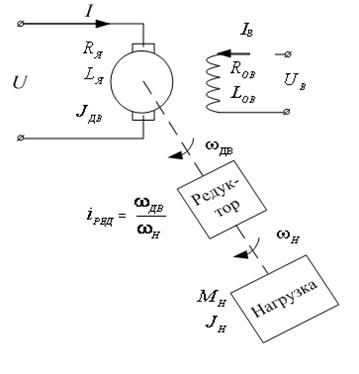
Рис. 2.1

На рисунке:

U, I – напряжение, приложенное к якорю и ток якоря;

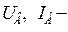напряжение и ток возбуждения;

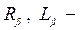сопротивление и индуктивность якорной обмотки. При включении в якорную цепь дополнительных индуктивностей и активных сопротивлений (при питании от усилителей); 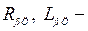общее активное сопротивление и индуктивность якорной цепи;

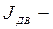момент инерции якоря двигателя;

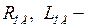сопротивление и индуктивность обмотки возбуждения;

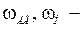частота вращения двигателя и нагрузки;

Ред. – редуктор (механическая передача) между двигателем и нагрузкой,

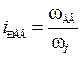передаточное отношение редуктора;

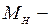статический момент сопротивления нагрузки;

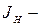момент инерции нагрузки.

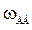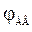Двигатель является сложным объектом, в котором протекают электрические, электромагнитные и механические процессы. Назначение – преобразование электрической энергии в механическую. Цели и задачи управления – регулирование частоты вращения или величины перемещения (угла поворота). Соответственно регулируемыми переменными будут механические координаты и (угол поворота). Возможные управляющие воздействия: 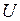, , 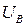магнитный поток 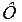, 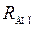– дополнительное сопротивление в якорной цепи.

Возмущения сигнальное – изменение величины момента нагрузки 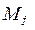, и параметрическое – изменение момента инерции нагрузки 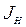. При определении математической модели нагрузку удобнее привести к валу двигателя. Полагая КПД редуктора равным единице из условия сохранения мощности можно записать

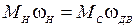или 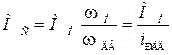, (2.1)

где 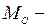момент сопротивления нагрузки, приведенный к валу двигателя.

Из условия сохранения кинетической энергии:

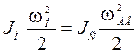или 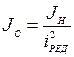, (2.2)

где 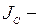момент инерции нагрузки, приведенный к валу двигателя.

Обозначим общий момент инерции всех движущихся масс

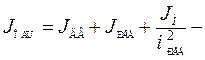. (2.3)

При использовании электродвигателей постоянного тока в подавляющем большинстве случаев осуществляют якорное управление изменением напряжения, приложенного к якорю двигателя. Полюсное управление (изменением магнитного потока 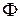) возможно только в сторону уменьшения магнитного потока, так как в номинальном режиме магнитная система двигателя близка к насыщению. Уменьшение 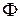позволяет регулировать скорость только в сторону увеличения (вверх от основной скорости). Реостатное регулирование путем введения дополнительного сопротивления в цепь якоря неэкономично и сильно ухудшает динамику электродвигателя.

При якорном управлении (двигатели с независим возбуждением или возбуждением от постоянных магнитов), когда магнитный поток остается постоянным 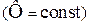, работа двигателя может быть описана системой четырех уравнений:

1) ;

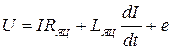2) 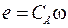; (2.4)

3) ;

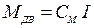4) ;

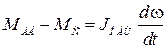или в операторной форме

1) ;

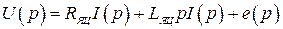2) 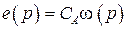; (2.5)

3) ;

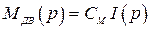4) ;

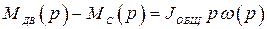в этих уравнениях 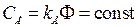, 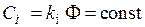– конструктивные постоянные двигателя.

Исключив из этих уравнений промежуточные переменные 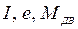, можем получить математическую модель 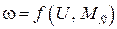при 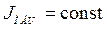в виде одного уравнения второго порядка:

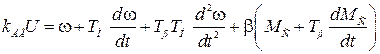, (2.6)

или в операторной форме

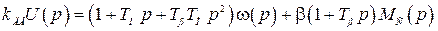. (2.7)

В этих уравнениях:

.

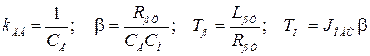Уравнение статики, описывающее установившийся режим, получим, положив производные равными нулю.

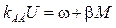. (2.8)

Это уравнение описывает механические характеристики двигателя, изображенные на рис. 2.2.

.

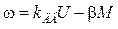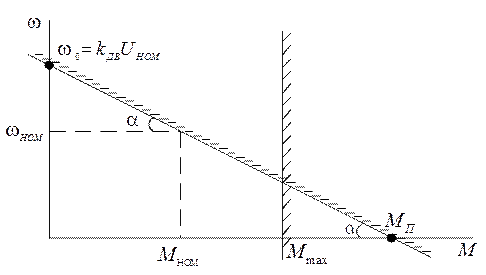
Рис. 2.2

Из механических характеристик наглядно виден физический смысл коэффициентов передачи по управляющему сигналу 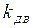и возмущению .

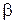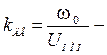коэффициент пропорциональности между частотой вращения 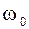и приложенным напряжением (при отсутствии нагрузки);

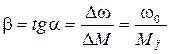– коэффициент наклона механических характеристик, характеризует изменение частоты вращения за счет изменения момента нагрузки.

Постоянные времени: 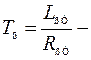электрическая постоянная времени якорной цепи, характеризует скорость изменения тока якоря при отсутствии ЭДС ( 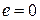), т.е. при заторможенном якоре; 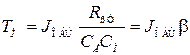– электромеханическая постоянная времени, характеризует скорость разгона двигателя (при ).

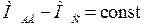Следует отметить, что при изменении момента инерции нагрузки ( 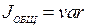) математическая модель будет с переменным параметром .

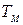Из операторного уравнения (2.7) легко получаются передаточные функции по управляющему сигналу и возмущению.

Положив 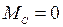, получим

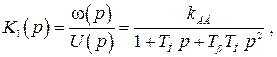(2.9)

при ,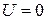

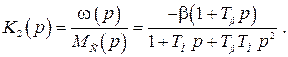(2.10)

При 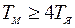корни знаменателя передаточных функции будут действительными и его можно разложить на два сомножителя:

,

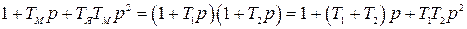Откуда

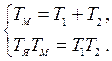
Решением этой системы уравнений будет

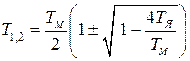, (2.11)

Математическая модель двигателя может быть представлена структурной схемой изображенной на рис. 2.3.

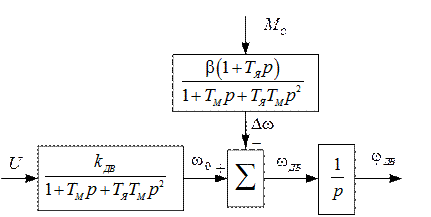
Рис. 2.3

Перенеся точку суммирования на вход, получим рис. 2.4.

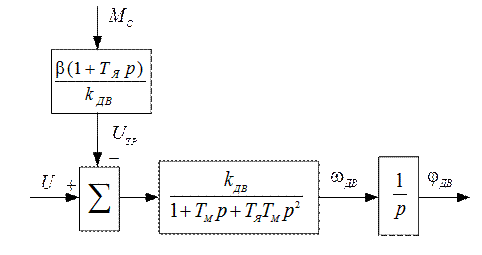
Рис. 2.4

Здесь 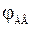– угол поворота вала двигателя; 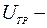напряжение трогания двигателя (зона нечувствительности), обусловленная наличием нагрузки на его валу.

Если 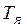мала (значительно меньше других постоянных времени в системе), математические модели можно упростить.

Считая 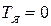можно записать:

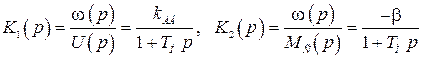. (2.12)

При расчете многоконтурных систем управления электроприводами, построеных по принципу систем подчиненного регулирования, с регуляторами тока, скорости и положения, воспользоваться этими моделями сложно, так как в них нет в явном виде тока якоря. Для расчета таких приводов удобно пользоваться моделью в виде структурной схемы с обратной связью по ЭДС двигателя.

Эта структура достаточно просто составляется по системе операторных уравнений (2.5).

1) ;

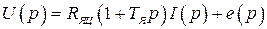2) ;

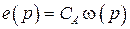3) ;

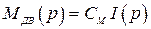4) ;

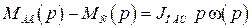из первого уравнения

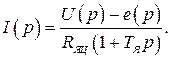
Структурная схема соответствующая этим уравнениям изображена на рис. 2.5.

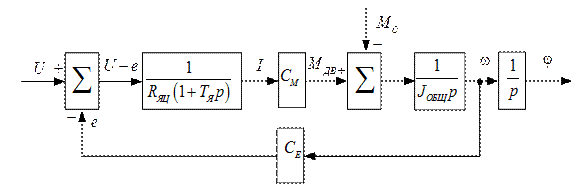
Рис. 2.5

Полученные математические модели описывают динамику любого двигателя постоянного тока при условии 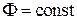. Для разных двигателей будут разными только параметры модели: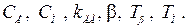

При расчете автоматических систем с такими двигателями можно воспользоваться любой из полученных математических моделей. Необходимо лишь вычислить ее параметры по справочным данным.

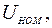
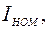
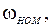
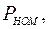
В справочных данных обычно указываются: 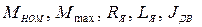. Из уравнения электрического равновесия якорной цепи в установившемся режиме работы 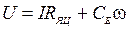находится конструктивная постоянная .

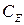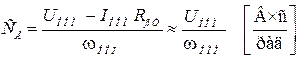. (2.14)

Конструктивная постоянная 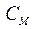находится из уравнения электромагнитного момента

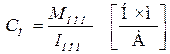. (2.15)

В указанных размерностях (в системе СИ) численные значения конструктивных постоянных теоретически равны. Практически 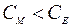, так как при ее вычислении используется значение номинального полезного момента на валу двигателя, который меньше электромагнитного.

Все остальные параметры вычисляются по выражениям, введенным при получении математической модели

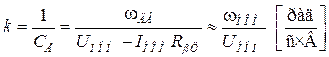(2.16)

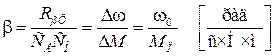(2.17)

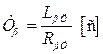. (2.18)

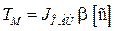. (2.19)

При вычислении параметров следует иметь в виду, что при полном использовании двигателя на номинальную мощность он будет нагреваться, вследствие чего сопротивление обмотки якоря будет возрастать

,

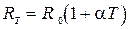где 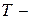температура перегрева;

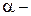температурный коэффициент сопротивления.

Для чистых металлов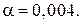

При допустимом для большинства двигателей перегреве 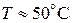, рабочее сопротивление якоря с учетом нагрева .

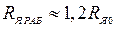2.2.3. Математическая модель крана. В простейшем случае модель крана представляется грузовой тележкой с электроприводом и подвешенным на тросе грузом. Налицо двухмассовая система с управляемой электроприводом тележкой и свободно болтающимся под ней грузом.

Если считать угол колебаний подвеса малым, то модель двухмассовой системы будет линейной. Таким образом, математическая модель крана можно представить в виде математического маятника, подвешенного на управляемой тележке. Если подвес сделать из жесткого стержня и перевернуть, получим модель неустойчивого маятника на управляемой тележке рис. 2.6.

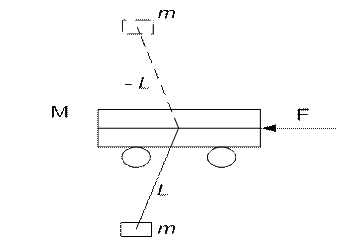
Рис. 2.6.

Такая модель соответствует движению пасажира на электрическом самокате, получившем в последнее время достаточно широкое распространение в качестве забавы и транспортного средства. Модели устойчивого и не устойчивого маятников для малых отклонений схожи и получаются одна из другой изменением знака длины подвеса.

Структура модели будет состоять из рассмотренной выше модели электродвигателя с дополнительной инерционностью тележки и консервативного звена, отражающего движение подвешенного груза. Квадрат частоты собственных колебаний подвеса будет определяться отношением ускорения силы тяжести g к длине подвеса L. Взаимное силовое воздействие тележки и груза в горизонтальной плоскости будет пропорционально смещению груза относительно точки подвеса. Ускорение тележки под действием груза будет зависеть от отношения массы груза m к массе тележки M.

С учетом того, что процессы управления замкнутым электроприводом с обратной связью по скорости значительно быстрее процессов колебаний подвеса, обычно пренебрегаем инерционностью электромагнитных процессов в электродвигателе и задаем модель электропривода инерционным звеном с полосой пропускания электропривода. Структурная схема модели изображена на рис. 2.7.

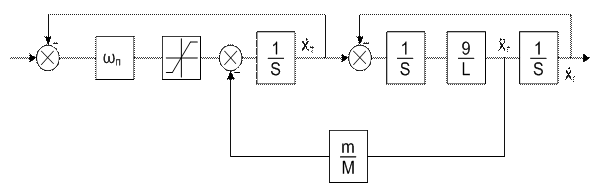
Рис. 2.7.

Чтобы учесть воздействие груза на привод тележки и возможное ограничение на ускорение электропривода, инерционное звено представляем в виде контура с единичной обратной связью. В прямой цепи контура включены последовательно: коэффициент равный полосе пропускания электропривода, ограничитель ускорения ненагруженной тележки, сумматор для подачи ускорения от груза через коэффициент m/M, интегратор. Выход интегратора – скорость тележки, вход – ее ускорение.

Консервативное звено подключаем к выходу электропривода и представляем также в виде контура с единичной обратной связью. В прямой цепи контура включены последовательно: интегратор 1, коэффициент равный g/L, интегратор 2. Ускорение от груза на привод подается со знаком минус через коэффициент m/M с выхода блока с коэффициентом g/L. Выход интегратора
1 – смещение груза относительно точки подвеса, выход интегратора 2 – скорость перемещения груза. Угловое смещение груза получается из линейного смещения делением на длину подвеса. Вход интегратора 2 – ускорение груза. Внешнее (ветровое) возмущение груза подаем на вход интегратрора 2 в виде силы, деленной на массу груза.

Двухмассовая модель груза. Если груз представляет собой протяженную конструкцию с возможностью колебаний относительно собственного центра масс, модель его движения может быть представлени в виде двух масс m1 и m2, связанных между собой еще одним подвесом длиной L2. К выше изложенной модели надо подключить еще одно консервативное звено (для нижней массы m2) к выходу скорости верхней массы m1. Воздействие нижней массы m2 на верхнюю m1 учитываем передачей ускорения с коэффициентом m2/m1.

Структурная схема модели изображена на рис. 2.8.

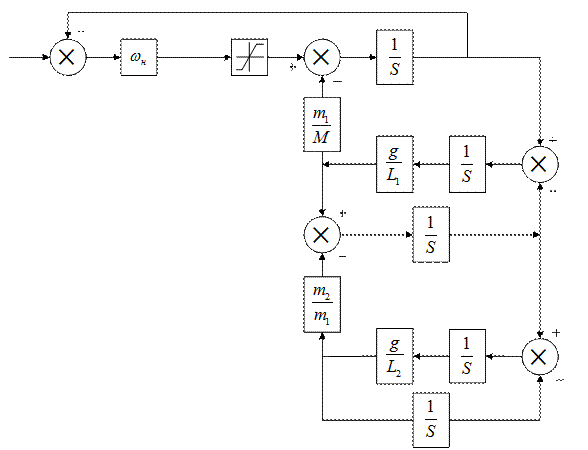
Рис. 2.8.

Модель груза в виде перевернутого маятника. Модель продольного движения электрического самоката с пасажиром получается из вышеизложенной модели крана подстановкой длины подвеса L со знаком минус. Контур управления продольным движением должен обеспечивать устойчивость движения, т.е. не опрокидывать пасажира, даже при его попытках специально опрокинуться.

2.2.4. Математическая модель транспортного робота (робокара). В автоматических транспортных системах ГАП для осуществления транспортных операций используются робокары. По принципу построения, т.е. по виду кинематической схемы их можно разделить на несколько групп:

1. Классическая четырехколесная с рулевым приводом.

2. Трехколесная, в которой переднее колесо является ведущим и рулевым (типа детского велосипеда).

3. Одноосная, в которой нет рулевого привода, а управление направлением движения осуществляется за счет разности скоростей движения ведущих колес, расположенных по бортам.

Последняя схема имеет существенные преимущества по сравнению с другими, обеспечивая симметрию движения вперед и назад и минимальные радиусы поворота, вплоть до разворота на месте. Кинематическая схема такого транспортного робота изображена на рис. 2.9.

Ведущие колеса 1 и 2 с индивидуальными силовыми приводами СП1 и СП2, расположены на оси симметрии по бортам. По углам установлены четыре опорных (флюгерных) колеса. Впереди и сзади на продольной оси симметрии расположены датчики трассы Д1 и Д2, выдающие сигнал, пропорциональный величине отклонения датчика от трассы.

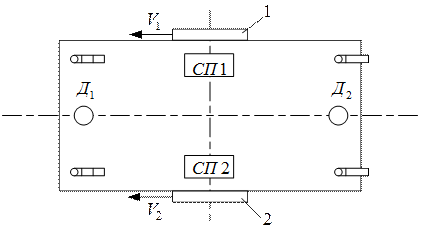
Рис. 2.9

Управление движением осуществляется бортовой системой программного управления. Верхний, программный уровень, который осуществляет:

1. Управление силовыми приводами (направление и скорость движения);

2. Выбор направления движения на разветвлениях трассы;

3. Управление приводом погрузочного-разгрузочного устройства (рольчанг, сталкиватель);

4. Фиксация груза во время движения;

5. Управление приводами тормозов.

Нижний уровень – следящая система – обеспечивает слежение за трассой, путем управления силовыми приводами по сигналу датчика трассы.

Скорость движения задается программно величиной задания на привода 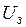. Слежение за трассой осуществляется по сигналу датчика 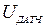, который суммируется с сигналом задания, обеспечивая отрицательную обратную связь.

.

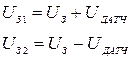Скорости вращения колес, пропорциональные сигналам задания, будут изменяться по сигналу датчика, стремясь удержать датчик над трассой.

Требуется определить математическую модель транспортного робота, связывающую отклонение датчика от трассы 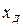с разностью скоростей вращения колес, которая является управляющим сигналом.

.

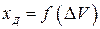При определении математической модели будем полагать, что колеса жесткие и отсутствует их проскальзывание во время движения.

Рассмотрим кинематику движения отдельных точек кара, изображенную на рис. 2.10.

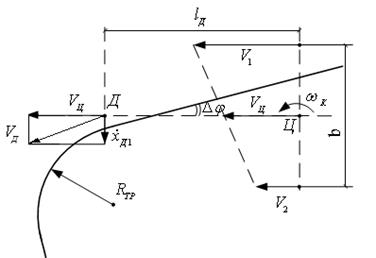
Рис. 2.10

На рисунке:

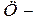центр кара;

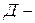точка установки датчика трассы;

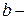база (ширина колеи);

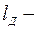вынос датчика от центра вперед;

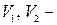скорости движения колес (бортов);

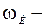угловая скорость разворота кара;

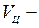заданная скорость движения.

Движение кара можно разделить на две составляющие: поступательное, направленное по продольной оси симметрии, и вращательное вокруг центра 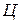. При совпадении направления продольной оси с направлением трассы поступательное движение не будет влиять на отклонение датчика. Отклонение же датчика будет определяться угловой скоростью разворота кара 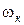и отличием направления движения кара от направления трассы. Для описания движения кара можно записать следующие уравнения:

1. Скорость движения центра кара, которая задается программно

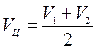. (2.21)

2. Угловая скорость разворота кара

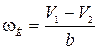. (2.22)

3. Линейная скорость перемещения датчика в направлении, перпендикуляром продольной оси за счет вращения кара

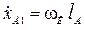. (2.23)

4. Линейная скорость перемещения датчика за счет отклонения направления движения от направления трассы

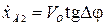. (2.24)

5. Отклонение направления движения кара от направления трассы

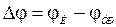, (2.25)

где 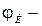направление движения кара;

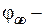направление трассы.

6. Суммарная скорость отклонения датчика от трассы

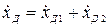. (2.26)

7. Величина отклонения датчика от трассы

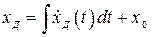. (2.27)

Изменение направления трассы происходит на поворотах трассы, которые выполняются по радиусам 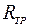. Для описания поворотов удобно ввести понятие угловой скорости поворота трассы:

8. 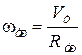. (2.28)

9. Разность угловых скоростей поворота кара и трассы

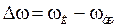. (2.29)

10. Разность направлений движения кара и трассы

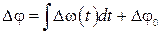. (2.30)

Записанная система уравнений позволяет представить математическую модель в виде структурной схемы рис. 2.10, входами которой являются разность скоростей колес 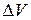и скорость поворота трассы 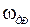, а выходом – отклонение датчика от трассы.

В процессе движения заданная скорость 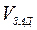поддерживается постоянной на отдельных интервалах движения (движение по прямой, поворот), что позволяет заменить множительное устройство умножением на постоянный коэффициент 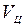. Разность направлений кара 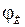и трассы 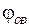обычно не превышает 10…15 градусов, поэтому приближенно можно считать 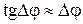. При этих допущениях модель становится линейной, изображенной на рис. 2.11.

При нулевых начальных условиях модель описывается передаточной функцией:

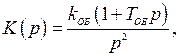(2.31)

где .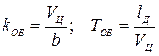

Анализ параметров математической модели показывает, что увеличение скорости движения 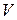увеличивает k_ОБ и уменьшает Т_ОБ, что делает его менее устойчивым. Изменение выноса датчика 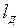также приводит к изменению устойчивости. При уменьшении 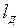уменьшается форсировка Т_ОБ, что также снижает устойчивость. При расположении датчика в центре кара ( 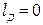) 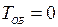и объект становится структурно неустойчивым.

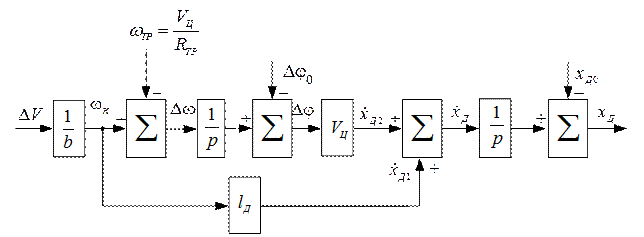
Рис. 2.11

2.2.5. Модели объектов с запаздыванием.Для описания процессов разнообразных промышленных объектов управления, включая химические реакторы, дистиляционные колонны, системы трубопроводов могут быть использованы модели с сосредоточенными параметрами и транспортным запаздыванием. Наличие запаздывания в контуре управления ведет к возрастанию фазового сдвига и тем самым сильно ограничивает полосу пропускания контура управления из-за опасности потери устойчивости. К этому следует добавить проблемы, связанные с недостоверностью описания объекта с распределенными параметрами моделью с постоянными сосредоточенными параметрами. Поэтому будет разумным использование моделей с сосредоточенными параметрами и транспортным запаздыванием с изменяющимися параметрами.

Передаточная функция чистого запаздывания представляет собой экспоненту, оперировать которой затруднительно. Например, передаточная функциея инерционного звена с запаздыванием имеет вид

.

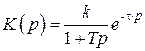На практике вместо экспоненты используют полиномиальную аппроксимацию запаздывания, имеющую похожую фазовую характеристику на низких частотах. Полиномы числителя и знаменателя аппроксимирующей передаточной функции имеют одинаковый порядок и одинаковые коэффициенты, но знаки у нечетных степеней полинома знаменателя отрицательны. Амплитудная характеристика для такой передаточной функции равна единице на всех частотах. Чем выше порядок полиномов, тем до более высоких частот выдерживается точность аппроксимации фазовой характеристики. Обычно ограничиваются аппроксимацией полиномом 1-го порядка. В Матлабе есть функция pade для вычисления аппраксимирующей запаздывание передаточной функции до 8-го порядка включительно.

2.2.6. Математические модели четырехполюсников. Для коррекции динамических свойств автоматических систем широко используются пассивные и активные электрические четырехполюсники. Их принципиальные электрические схемы, частотные характеристики и расчетные соотношения для расчета параметров приводятся в справочной литературе. Однако следует иметь в виду, что приводимые расчетные соотношения соответствуют работе четырехполюсника на холостом ходу, когда сопротивление нагрузки значительно больше выходного сопротивления четырехполюсника. Кроме того, типовые корректирующие четырехполюсники не всегда обеспечивают получение требуемых частотных характеристик. В связи с этим возникает необходимость определить передаточную функцию и частотные характеристики по принципиальной электрической схеме.

Эта задача может быть решена путем описания процессов, происходящих в схеме, известными законами электротехники (Ома, Кирхгоффа). Рассмотрим это на примере дифференцирующего звена, схема которого приведена на рис. 2.12.

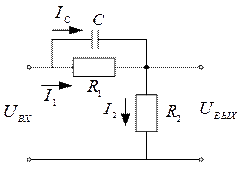
Рис. 2.12

Для этой схемы можно записать систему уравнений:

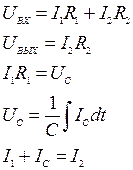
Исключив промежуточные переменные из этой системы уравнений, можем получить интересующую нас передаточную функцию

.

Однако эта задача может быть решена значительно проще, если воспользоваться операторными выражениями для сопротивлений элементов схемы. Представим схему, изображенную на рис. 2.13, в виде Г-образного четырехполюсника, который представляет собой делитель напряжения.

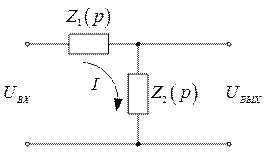
Рис. 2.13

Для этого делителя

1) .

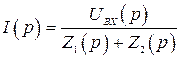2) .

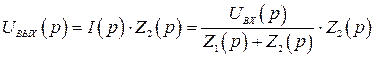Передаточная функция четырехполюсника:

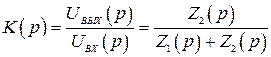. (2.32)

Для определения передаточной функции достаточно знать выражения комплексных сопротивлений для индуктивности 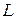( 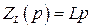), емкости 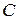( 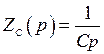) и активного сопротивления 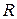( 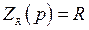) и правила определения сопротивлений при параллельном и последовательном соединении элементов. Так для рассматриваемого примера:

;

;

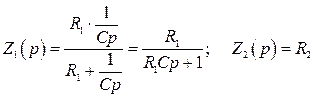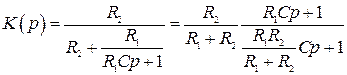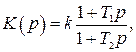
где .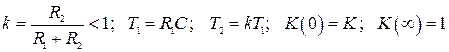

ЛАХ четырехполюсника приведена на рис. 2.14.

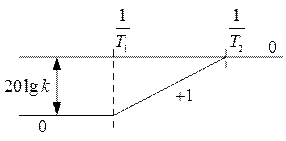
Рис. 2.14

Активные четырехполюсники реализуются на операционных усилителях, которые могут быть включены по инвертирующей или неинвертирующей схемам, изображенным на рис. 2.15 и 2.16 соответственно. В активных четырехполюсниках используется свойство операционного усилителя за счет большого коэффициента усиления и соответственно очень малого дифференциального напряжения входов, развязывать объединенные инвертирующим входом цепи, входную цепь и цепь обратной связи. Передаточная функция записывается как отношение операторных (комплексных) сопротивлений цепей, обратной связи и входной.

Операционные усилители обязательно балансируются по постоянному току включенным между неинвертирующим входом и землей резистором Rb, проводимость которого равна суммарной проводимости (постоянному току) всех цепей, соединенных с инвертирующим входом.

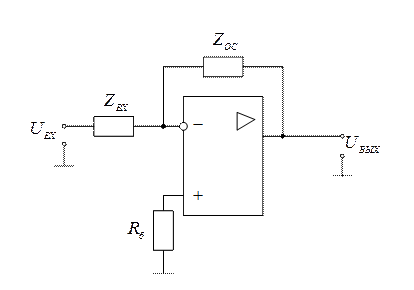
Рис. 2.15. Инвертирующая схема включения

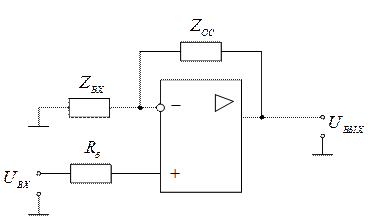
Рис. 2.16. Неинвертирущая схема включения

Передаточная функция активного четырехполюсника определяется так же отношением комплексных сопротивлений.

Для инвертирующей схемы

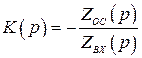. (2.33)

Для неинвертирующей схемы

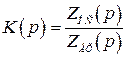. (2.34)

В этих схемах 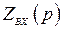и 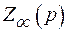могут представлять собой сложные схемы, состоящие из многих элементов. Подбирая соответствующие элементы можно получить требуемые передаточные функции.

Следует отметить, что при определении передаточных функций необходимо вначале решить задачу в общем виде, затем ввести обозначения параметров через 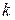и 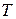, и только потом вычислить численные значения этих параметров. Это позволит значительно сократить количество ошибок при определении математических моделей.

2.3. Определение математических моделей
по экспериментальным данным

Экспериментальные методы применяются в тех случаях, когда получить математическую модель аналитически затруднительно (например, из–за сложности и недостаточной изученности процессов, происходящих в объекте), а также для проверки и уточнения математических моделей, полученных аналитически.

Создание точной рабочей модели сложного объекта без экспериментальной проверки и доводки практически невозможно, так как аналитическая модель бывает либо недостаточно точной и надежной, либо очень сложной и громоздкой.

Задача эксперимента состоит в получении упрощенных функциональных связей между интересующими переменными процесса. Критерием подбора таких упрощенных функций является минимизация отклонения реакции в модели от реакции в реальном объекте.

Эксперимент может быть активным и пассивным.

При а<