Кинетическая энергия тела
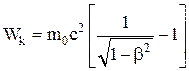 .
.
Полная энергия тела складывается из внутренней энергии и кинетической энергии тела как целого:
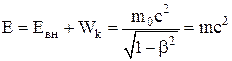 ,
,
где 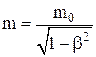 – релятивистская масса.
– релятивистская масса.
Энергия связи системы каких-либо частиц– работа, затраченная на разделение системы на составляющие ее частицы и удаление их друг от друга на такое расстояние, на котором их взаимодействием можно пренебречь:
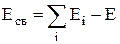 ,
,
где Eсв – энергия связи;
åEi – сумма энергий разделенных частиц системы;
E – энергия системы.
Сумма масс разделенных частиц больше массы системы на величину энергии связи, деленную на c2:
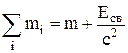 .
.
Дефект массы Dm – разность между суммой масс частиц и массой системы:
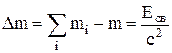 .
.
Закон взаимосвязи массы и энергии:
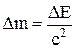 , E = mc2.
, E = mc2.
Закон изменения импульса-энергии материальной точки:
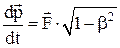 .
.
Закон изменения энергии материальной точки:
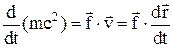 .
.
Закон изменения кинетической энергии тела:
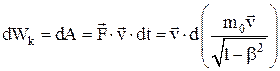 .
.
Соотношение, связывающее полную энергию и импульс релятивистской частицы (в векторной форме):
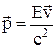 .
.
Связь между импульсом и полной энергией в скалярной форме:
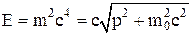 .
.
Связь между импульсом и кинетической энергией:
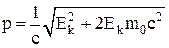 .
.
Для частиц с нулевой массой покояэнергия пропорциональна импульсу:
E = c×p; p = E/c.
Кинетическая масса частиц, которые не обладают массой покоя, равна полной энергии:
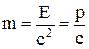 .
.
Приложение 2
Основы молекулярной физики
и термодинамики. Основные понятия, определения и законы
Конденсированное состояние. Кинематика
и динамика жидкостей
Жидкость – агрегатное состояние вещества, промежуточное между твердым и газообразным состояниями.
Чистые жидкости по химическому составу – однокомпонентные жидкости.
Жидкие смеси (растворы) по химическому составу – двух- или многокомпонентные жидкости.
Нормальные (обычные) жидкости – однородные макроскопические и изотропные жидкости. При отсутствии внешних воздействий обладают только одной жидкой фазой.
Квантовые жидкости – жидкости, которые могут находиться в нормальной и одной или нескольких анизотропных фазах.
Простые жидкости – жидкости, состоящие из сферически симметричных молекул, между которыми действуют силы Ван-дер-Ваальса, не имеющие какого-либо преимущественного направления и обладающие наиболее простыми свойствами.
Ближний порядок – упорядоченное расположение по отношению к любой молекуле ближайших к ней соседей.
Зависимость между временем t одного колебания молекулы относительно данного положения и временем «оседлой» жизни t0:
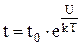
где U – «потенциальный барьер», численно равный разности энергий молекулы в двух возможных областях ее колебаний, разделяющий две возможные области колебаний молекулы;
Т – температура жидкости;
k – постоянная Больцмана.
Число молекул жидкости в некотором сферическом слое толщиной dr на расстоянии r от произвольно выбранной молекулы
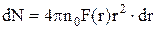 ,
,
где n0 = N/V – число молекул в единице объема жидкости;
F(r) – радиальная функция распределения, которая определяет вероятность нахождения некоторой молекулы жидкости в какой-либо точке ее объема.
Вязкость – свойство жидкостей оказывать сопротивление перемещению одной их части относительно другой. Определяется их молекулярным составом и строением.
Основной закон вязкого течения (закон Ньютона):
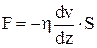 ,
,
где dv/dz – градиент скорости в направлении z;
S – площадь слоя, по которому происходит сдвиг;
h – коэффициент динамической вязкости, который характеризует сопротивление жидкости смещению ее слоев.
Зависимость коэффициента вязкости жидкостей от температуры:
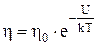 ,
,
где U – энергия, необходимая для перехода молекулы жидкости из одного равновесного состояния в другое.
Кинематическая вязкость – отношение динамической вязкости к плотности жидкости:
n = h/r.
Текучесть жидкостей – свойство, обратное вязкости, обусловлено той свободой движения молекул в объеме, которая еще допускается силами сцепления между ними.
Коэффициент текучести (или текучесть)
j = 1/h.
Сжимаемость – способность жидкости изменять свой объем под действием всестороннего давления.
Коэффициент сжимаемости – выражает уменьшение единичного объема (или плотности) при увеличении давления на единицу:
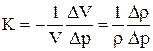 ,
,
где DV, Dρ – изменение первоначального объема и первоначальной плотности жидкости при изменении давления на Dp.
Уравнение состояния жидкости (с определенной степенью точности):
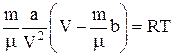 .
.
Сфера действия молекулярных сил – область, в которой расположены взаимодействующие молекулы, в центре которой находится рассматриваемая молекула (R ~ 10-9 м).
Экспериментальный закон зависимости объема жидкости от температуры:
Vt = V0(1 + at),
где a – коэффициент объемного расширения, который определяется соотношением
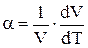 .
.
Связь коэффициентов сжимаемости и объемного расширения жидкостей:
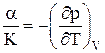 .
.
Поверхностное натяжение – мера некомпенсированности межмолекулярных сил в поверхностном (межфазном) слое.
Работа dA по изменению поверхности жидкости на dS совершается за счет изменения потенциальной энергии поверхностного слоя (поверхностной энергии жидкости) dWps:
dA = –dWps = –s×dS,
где «минус» показывает, что увеличение поверхности жидкости сопровождается совершением работы;
s – коэффициент поверхностного натяжения, который характеризует свойства поверхности жидкости и показывает, какую работу необходимо совершить, чтобы увеличить поверхность жидкости на единицу.
Работа по изменению поверхности жидкости, совершаемая внешними силами:
dA = –F×dx = –s×dS = –sℓ×dx,
где ℓ – длина контура, охватывающего поверхность жидкости;
dx – смещение границы поверхностного слоя;
F – сила поверхностного натяжения;
s – коэффициент поверхностного натяжения, который численно равен силе поверхностного натяжения, стремящейся изменить длину контура, охватывающего поверхность жидкости, на единицу.
Зависимость коэффициента поверхностного натяжения от температуры:
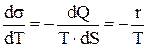 ,
,
где r = dQ/dS – количество тепла, затраченное на изменение поверхности пленки на единицу.
Полное молекулярное давление в поверхностном слое жидкости
p = p0 ± Dp,
где p0 – молекулярное давление жидкости с плоской поверхностью;
Dp – дополнительное давление, возникающее за счет кривизны поверхности жидкости;
знак «+» – соответствует выпуклой поверхности;
знак «–» – соответствует вогнутой поверхности.
Формула Лапласа для дополнительного давления (для капли, которая полностью заполнена жидкостью, или для пузырька внутри жидкости) в случае:
1) произвольной поверхности:
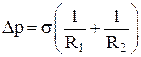 ,
,
где R1 и R2 – радиусы кривизны поверхностного слоя жидкости;
2) сферической поверхности:
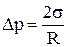 ,
,
где R – радиус сферы;
3) цилиндрической поверхности:
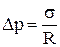 ,
,
где R – радиус цилиндрической поверхности.
Формула Лапласа для дополнительного давления (для пузырька, который не заполнен жидкостью, например мыльного) в случае:
1) сферической поверхности:
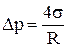 ;
;
2) цилиндрической поверхности:
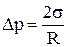 .
.
Условие равновесия капли на поверхности другой жидкости:
s12 + s23 = s13,
где s12 – коэффициент поверхностного натяжения между жидкостью капли и жидкостью, на которой она находится;
s13 – коэффициент поверхностного натяжения между жидкостью, на которой находится капля, и воздухом;
s23 – коэффициент поверхностного натяжения между жидкостью капли и воздухом.
Условие равновесия капли на поверхности твердого тела:
s12 + s23×cosq = s13,
где s12 – коэффициент поверхностного натяжения между жидкостью капли и твердым телом;
s13 – коэффициент поверхностного натяжения между твердым телом и воздухом;
s23 – коэффициент поверхностного натяжения между жидкостью капли и воздухом;
q – краевой угол (угол между касательными к поверхности жидкости и твердого тела).
Условие смачивания (краевой угол острый):
s12 + s23×cosq £ s13.
Условие абсолютного смачивания:
s12 + s23×cosq < s13.
Условие несмачивания (краевой угол тупой):
s12 ³ s23×cosq + s13.
Условие абсолютного несмачивания:
s12 > s23×cosq + s13.
Капиллярные явления (капиллярность) – изменение высоты уровня жидкости в узких трубах (капиллярах) или зазорах между двумя стенками.
Условие капиллярности:
Dp = p,
где 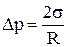 – дополнительное давление, возникающее за счет кривизны поверхности жидкости при капиллярности;
– дополнительное давление, возникающее за счет кривизны поверхности жидкости при капиллярности;
p = rgh – давление;
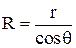 – радиус мениска;
– радиус мениска;
r – радиус капилляра;
q – краевой угол.
Высота подъема (опускания) жидкости в капиллярах
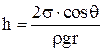 .
.
Высота подъема (опускания) жидкости в узком зазоре между погруженными в жидкость параллельными пластинами
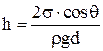 ,
,
где d – расстояние между пластинами.
Давление внутри жидкости во всех точках, расположенных на одном уровне (при механическом равновесии, если жидкость находится в поле тяготения):
p = const.
Давление в жидкости на двух разных уровнях (при механическом равновесии; жидкость находится в поле тяготения) отличается на величину, равную весу вертикального столба жидкости, заключенного между этими уровнями, с площадью сечения, равного единице:
p2 = p1 + rgh,
где p1, p2 – давления жидкости на соответствующих уровнях;
h – высота между слоями.
Закон Архимеда: «На тело, погруженное в жидкость (или газ), находящееся в механическом равновесии, действует выталкивающая сила, равная весу вытесненной телом жидкости (газа), направленная по вертикали вверх и приложенная к центру масс вытесненного объема»:
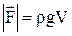 .
.
Поток жидкости – совокупность частиц движущейся жидкости.
Линия тока жидкости – линия, касательная к которой совпадает с направлением скорости частицы жидкости в рассматриваемый момент времени и в данной точке пространства. Линии тока жидкости служат для графического отображения потока жидкости.
Трубка тока – часть жидкости, ограниченная линиями тока.
Установившееся (стационарное) течение жидкости – движение жидкости, при котором форма и расположение линий тока, а также значения скоростей частиц жидкости в каждой их точке не изменяются со временем.
Неустановившееся (нестационарное) течение жидкости – движение жидкости, при котором не выполняются условия стационарного движения.
Математическая форма записи теоремы (уравнения) о неразрывности (непрерывности струи) для несжимаемой жидкости:
Sv = const,
где S – площадь сечения трубки тока;
v – скорость жидкости.
Уравнение Бернулли для стационарно текущей идеальной жидкости (для жидкостей с малой вязкостью):
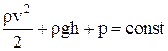 ,
,
где r – плотность жидкости;
v – скорость течения жидкости;
h – высота, на которой находится некоторое сечение трубки тока;
p – давление жидкости на уровне этих сечений.
Закон изменение давления жидкости для двух сечений (с изменением высоты h сечений) при v1 = v2:
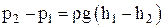 .
.
Закон изменение давления жидкости для горизонтального потока (h1 = h2):
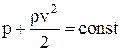 ,
,
где p – давление, не зависящее от скорости (статическое давление жидкости);
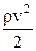 – давление, зависящее от скорости (динамическое давление), которое показывает, на какую величину изменяется статическое давление при остановке движущегося потока жидкости.
– давление, зависящее от скорости (динамическое давление), которое показывает, на какую величину изменяется статическое давление при остановке движущегося потока жидкости.
Полное давление потока жидкости – сумма статического и динамического давлений.
Монометрические трубки (трубки Пито) – приборы, с помощью которых измеряют статическое и полное давление жидкости.
Скорость течения вязкой жидкости в трубе
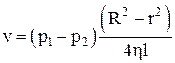 ,
,
где p1, p2 – давления двух сечений трубы;
R – радиус трубы;
r – расстояние от центра трубы до рассматриваемой трубки тока;
h – коэффициент вязкости жидкости;
l – расстояние между сечениями трубы.
Формула Пуазейля для определения объема жидкости, прошедшего через сечения трубы:
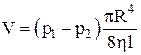 .
.
Ламинарное (слоистое) течение жидкости – когда жидкость как бы разделяется на слои, скользящие относительно друг друга, не перемешиваясь. Ламинарное течение жидкости стационарно.
Турбулентное течение жидкости – когда происходит энергичное перемешивание жидкости. В этом случае скорость частиц в каждом месте изменяется хаотично, течение – нестационарное.
Число Рейнольдса определяет характер течения жидкости:
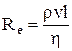 ,
, 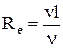 ,
,
где r – плотность жидкости;
v – средняя по сечению скорость движения жидкости;
l – характерный для поперечного сечения размер;
h – динамическая вязкость;
n – кинематическая вязкость.
Основные понятия, определения и законы
молекулярной физики и термодинамики
Молекулярная физика – раздел физики, в котором изучаются физические свойства и строение вещества в различных агрегатных состояниях на основе их микроскопического (молекулярного) строения.
Молекулярно-кинетическая теория строения вещества – раздел молекулярной физики, в котором изучаются свойства тел на основе представлений об их молекулярном строении.
Статистическая физика – раздел молекулярной физики, в котором изучаются свойства и движения не отдельных молекул (частиц), а совокупности частиц, характеризующихся средними величинами.
Термодинамика – наука, в которой изучаются свойства физических систем вне связи с их микроскопическим строением.
Молекула – наименьшая часть вещества, обладающая его основными химическими свойствами и состоящая из атомов, соединенных между собой химическими связями.
Атом – наименьшая частица химического элемента (микрочастица), обладающая его свойствами. Атомы в разных сочетаниях входят в состав молекул разных веществ.
Относительная атомная масса – отношение массы данного атома к 1/12 массы изотопа углерода с массовым числом 12 (12С).
Относительная молекулярная масса – отношение массы данной молекулы к 1/12 массы атома 12С.
Моль – количество вещества, в котором содержится число частиц, равное числу атомов в 0,012 кг изотопа углерода С12.
Число Авогадро – число атомов или молекул в моле любого вещества: NА = 6,02×1023 моль-1.
Молярная масса – масса вещества, взятого в количестве одного моля:
m = m0×NА.
Идеальный газ – теоретическая модель газа, в которой не учитывается взаимодействие его частиц (средняя кинетическая энергия частиц много больше энергии их взаимодействия). Размеры молекул идеального газа малы по сравнению с расстояниями между ними. Суммарный собственный объем молекул такого газа мал по сравнению с объемом сосуда. Силы взаимодействия между молекулами настолько малы, что движение молекул от столкновения до столкновения происходит по прямолинейным отрезкам. Число ежесекундных столкновений молекул велико.
Основные положения молекулярно-кинетической теории идеального газа:
1) газ состоит из мельчайших частиц – атомов или молекул, находящихся в непрерывном движении;
2) в любом, даже очень малом объёме, к которому применимы выводы молекулярно–кинетической теории, число молекул очень велико;
3) размеры молекул малы по сравнению с расстояниями между ними;
4) молекулы газа свободно движутся между двумя последовательными взаимодействиями друг с другом или со стенками сосуда, в котором он находится. Силы взаимодействия между молекулами, кроме моментов соударения, пренебрежимо малы. Соударения молекул происходят без потерь механической энергии, т.е. по закону абсолютно упругого взаимодействия;
5) при отсутствии внешних сил молекулы газа распределяются равномерно по всему объёму;
6) направления и значения скоростей молекул газа самые различные.
Основное уравнение молекулярно-кинетической теории газов:
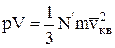 ,
,
где 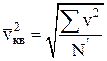 – средняя квадратичная скорость.
– средняя квадратичная скорость.
Основное уравнение молекулярно-кинетической теории газов для давления:
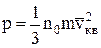 , или
, или 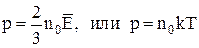 ,
,
где n0 – N'/V – число молекул в единице объема;
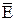 – средняя кинетическая энергия поступательного движения молекул газа;
– средняя кинетическая энергия поступательного движения молекул газа;
k – постоянная Больцмана.
Закон Авогадро: «В одинаковых объемах при одинаковых температурах и давлениях содержатся одинаковые количества молекул».
Закон Дальтона: «Давление смеси газов равно сумме парциальных давлений, т.е. тех давлений, которые имел бы каждый из входящих в смесь газов, если бы в объеме, занятом смесью, находился он один»:
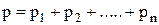 .
.
Уравнение состояния идеальных газов для произвольной массы m (уравнение Менделева–Клапейрона):
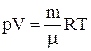 ,
,
где R – газовая постоянная, которая численно равна работе расширения одного моля газа при его нагревании на один градус в условиях постоянного давления;
T – абсолютная температура.
Степени свободыi – число независимых координат, необходимых для полного описания положения системы в пространстве. Все степени свободы равноправны.
Дата добавления: 2022-02-05; просмотров: 461;











