Ускорение в четырехмерной системе отсчета

<16 17 181920 21 22 >

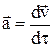Кинематические уравнения движения в четырехмерной системе отсчета(по известному а(t) можно найти v(t) и S(t)):

, .

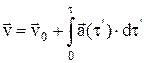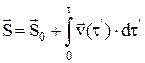Формулы преобразования координат при переходе из одной системы отсчета в другую (преобразования Г.А. Лоренца):

а) обратные:

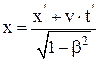; у = у^'; z = z^'; ;

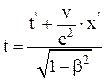б) прямые:

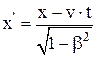; у = у^'; z = z^'; .

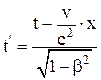Следствия из преобразований Лоренца:

а) закон сложения скоростей (в частном случае, когда скорость u направлена вдоль оси OX):

;

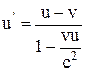б) сокращение продольных движущихся масштабов длин сокращения (Лоренца):

; ,

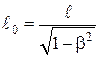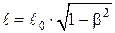где ℓ₀ – длина стержня в той системе отсчета, в которой он покоится;

ℓ – длина стержня в системе отсчета, движущейся относительно стержня;

в) замедление хода движущихся часов:

; ,

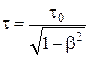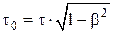где τ₀ = t₂^' – t₁^' – промежуток времени, прошедший между этими событиями, в подвижной системе К^';

τ = t₂ – t₁ – промежуток времени, прошедший между этими событиями, в неподвижной системе К.

Первый закон Ньютона в специальной теории относительности устанавливает существование в природе систем отсчета, сколь угодно близких к инерциальным системам отсчета. Такими системами отсчета являются те, в которых свободное тело не имеет по отношению к ним ускорения.

<16 17 181920 21 22 >

Дата добавления: 2022-02-05; просмотров: 182;