Линейная зависимость и независимость векторов линейного пространства.

Линейные (векторные) пространства.

Определение: Множество L называется линейным (векторным) пространством, если на нем введены две операции:

1) сложение: для любых х, у Є L сумма (х + у) Є L,

2) умножение на число: для любого х Є L и любого числа λ произведение

λх Є L,

которые удовлетворяют 8 аксиомам:

1) х + у = у + х, где х,у Є L;

2) (х + у)+z = x+(у + z), где х,у,z Є L;

3) существует нулевой элемент Ө такой, что Ө + х = х, где х Є L;

4) для любого х Є L существует единственный противоположный элемент

(–х) такой, что х + (-х)= Ө;

5) 1·х = х, где х Є L;

6) α(βх) = (αβ)х, где х Є L, α и β- числа;

7) α(х + у) = αх + αу, где х,у Є L, α- число;

8) (α + β) х = αх + βх, где х Є L, α и β- числа.

Замечание: Элементы линейного (векторного) пространства называют векторами.

Примеры:

Множество действительных чисел является линейным пространством.

Множества всех векторов на плоскости и в пространстве являются линейным пространством.

Множество всех матриц одного размера является линейным пространством.

Линейная зависимость и независимость векторов линейного пространства.

Дана в линейном пространстве система векторов а_1, а_2, а_{3, …} а_n Є L.

Определение: Вектор α₁ а₁+ α₂ а₂+…+ α_n а_n Є L, где α_i (i = 1,…,n) - числа, называется линейной комбинацией (ЛК) векторов а_1, а_2, а_{3, …} а_n.

Определение: Система векторов линейного пространства а_1, а_2, а_{3, …} а_n Є L называется линейно независимой (ЛНЗ), если линейная комбинация

α₁ а₁+ α₂ а₂+α₃ а₃+…+ α_n а_n=0 тогда и только тогда, когда коэффициенты

α ₁ =α ₂ =α ₃ =…=α _n=0.

Определение: Система векторов а_1, а_2, а_{3, …} а_n Є L называется линейно зависимой (ЛЗ), если существует набор чисел α_1, α₂ ,α₃ … α_n, не все из которых равны 0, такие что линейная комбинация α₁ а₁+ α₂ а₂+…+ α_n а_n= 0.

Примеры:

Два вектора называются коллинеарными, если они параллельны одной прямой или лежат на одной прямой.

1) Рассмотрим два ненулевых, неколлинеарных вектора на плоскости. Диагональ 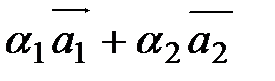=0 .

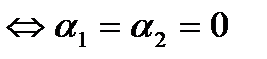α2а2

α1а1+α2а2

а₁ α₁ а₁

Два ненулевых, не коллинеарных вектора на плоскости линейно независимы.

2) Рассмотрим два ненулевых , коллинеарных вектора а₁ ║а₂.

а1

а2

Линейная комбинация равна нулю, есть не нулевой коэффициент, следовательно, два коллинеарных вектора на плоскости линейно зависимы.