ВВЕДЕНИЕ В ТЕОРИЮ АЛГОРИТМОВ.

Слово алгоритм (algorithm) происходит от имени среднеазиатского ученого средневековья Муххамад ибн Мусаал-Хорезми ( Магомет, сын Моисея, из Хорезма (Узбекистан) (жил с 783 по 850 гг.)) В 1983 году отмечалось 1200-летие со дня его рождения. В Европе слово алгоритм использовалось для обозначения произвольных вычислительных процессов.

Вплоть до 30-х годов нашего столетия понятие алгоритма оставалось интуитивно понятным, имевшем скорее методологическое, а не математическое значение. Вместе с тем уже древние греки обнаружили ряд проблем, для которых им не удалось построить алгоритм (или разрешающую процедуру). Такими проблемами были проблема разбиения произвольного угла на три равных угла с помощью циркуля и линейки, проблема построения круга, равновеликого заданному квадрату, проблема отыскания рациональных корней произвольного диофантова уравнения, например, .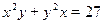

Решение таких проблем потребовало привлечения новых логических средств.

С понятием алгоритма связывали последовательность операций, которая могла быть охарактеризована такими свойствами как

q массовость

q повторяемость

q детерминизм

Массовость означала возможность использовать алгоритм для решения целого круга задач в рамках некоторой общей проблемы.

Повторяемость означает получение одного и того же результата для одних и тех же данных.

Детерминизм означает, что шаги алгоритма не оставляют двусмысленности и выбор каждого последующего шага определен однозначно.

В конце 17 в. немецкий ученый Г.В. Лейбниц выдвинул идею об универсальной характеристике, т.е. об универсальном решателе задач. Для реализации своей идеи Лейбниц ввел язык для записи задач, который можно назвать прообразом языка логики первого порядка. Лейбницу не удалось создать универсальный алгоритм. Идея универсализма долгое время притягивала умы людей не только в сфере науки (укажем, например, идею вечного двигателя, универсального растворителя, эликсира молодости, философского камня для преобразования ртути в золото и др.)

Существенным толчком в деле разработки точного математического понятия алгоритма была поставленная великим немецким математиком Д.Гильбертом задача построения доказательства произвольной формулы, выразимой в языке данной формальной теории, средствами этой теории.

Точное математически строгое определение алгоритма сформулировал английский ученый Алан Тьюринг.

Параллельно Тьюрингу такие ученые как С.Клини, А.Черч, К.Гедель и другие рассматривали проблему представления вычислимых функций с точки зрения их записи из некоторых простейших функций. Они ввели в рассмотрение класс рекурсивных и частично-рекурсивных функций. Знаменитый тезис Черча утверждает, что класс частично-рекурсивных функций и класс частично-вычислимых функций суть один и тот же класс.

Оба данных подхода, а также другие подходы ( Марков, Пост ) привели к одному и тому же классу алгоритмически вычислимых функций и подтвердили целесообразность использования тезиса Черча. Таким образом, сформировался круг понятий теории алгоритмов, важнейшими из которых являются вычислимая функция, рекурсивность (частичная рекурсивность), рекурсивная перечислимость, рекурсивная сводимость, алгоритмическая и вычислительная сложность и др.

На этом фундаменте были получены важные теоретические результаты. Сначала К.Гедель опроверг идею Гильберта, доказав существование в арифметике целых чисел теорем, которые выразимы средствами теории, но не доказуемы и не опровержимы в ней. Затем А.Черч получил аналогичный результат для логики первого порядка. Новиковым П.С. в 1952 году было получено решение классической проблемы тождества для конечно-определенных групп, сформулированной Деном в 1912 году. Знаменитая десятая проблема Гильберта, сформулированная им в 1900 году (о разрешимости диофантова уравнения) была отрицательно решена в 1970 году советским математиком Мятиясевичем Ю.В.

Важнейшими задачами теории алгоритмов являются следующие:

q доказательство алгоритмической разрешимости/неразрешимости проблемы;

q построение эффективного алгоритма или доказательство, что такого алгоритма нет;

q анализ сложности алгоритма;

q разработка языков спецификации алгоритмов и задач;

q проблема построения сведения одних задач к другим; и др.

Проблема построения эффективных алгоритмов имеет прямое отношение к практике. Оказалось, что существует целый класс важных для практики задач, для которых до настоящего времени не удалось найти хороших решающих процедур. Более того, для этих задач нет даже приближенных алгоритмов. Классы этих задач известны как классы NP-полных и NP-трудных задач.

Начала складываться так называемая метрическая теория алгоритмов, основным содержанием которой является классификация задач по классам сложности. Сами алгоритмы стали объектом точного исследования, как и те объекты, для работы с которыми они предназначены. Важно отыскание как верхних, так и нижних, и средних оценок сложности вычислений. Важным в практическом плане результатом было построение Л.Г.Хачияном полиномиального по сложности алгоритма для решения задачи линейного программирования, поскольку было показано, что симплексный алгоритм имеет в худшем случае экспоненциальную оценку вычислительной сложности, хотя в среднем ведет себя хорошо. Разработанный Хачияном метод эллипсоидов был развит и для решения задач так называемого выпуклого программирования. С иных позиций полиномиальный алгоритм для задачи линейного программирования разработал американский ученый индийского происхождения Н.Кармаркар.

Установить нижнюю оценку – значит доказать, что никакой алгоритм вычисления не имеет сложности меньшей, чем заданная граница. Для получения результатов такого типа необходима точная фиксация рассматриваемой алгоритмической модели, и такие результаты получены только в очень жестких вычислительных моделях.

Имеются ли модели, альтернативные машинам Тьюринга как формализации понятия алгоритма? Нам известна одна модель такого рода - модель персептрона (нейрона). Можно сказать, что персептрон угадывает (распознает) ответ, не решая задачу как таковую. Распознающая функция персептрона строится в процессе обучения, так что нет доказательства, что персептрон не может ошибиться на какой-нибудь очередной задаче. Собственно, и для алгоритмов актуальна проблема построения доказательства того, что они правильно решают задачу. Поэтому уместно назвать алгоритмы, для которых требуемые доказательства имеются – доказательно конструируемыми алгоритмами. Однако возможны случаи, когда алгоритм есть, но нет доказательства его корректности (под корректностью здесь понимаем правильность работы алгоритма).

Итак, решение задач связано с построением алгоритмов. Первое, что нужно выяснить, можно ли вообще построить алгоритм? Далее разработчику важно построить хороший (эффективный) алгоритм или обосновать его эффективность в среднем. Если хороший алгоритм построить не удается, то уместно выяснить, нельзя ли построить приближенный алгоритм или эвристический алгоритм. Для эвристических алгоритмов проблема состоит в обеспечении их статистической эффективности.