ЛЕКЦИЯ 7. ПОНЯТИЕ ВЫЧИСЛИТЕЛЬНОЙ СЛОЖНОСТИ.

Аппарат машин Тьюринга позволяет изучить сложностные свойства алгоритмов. В информатике имеется несколько различных подходов к определению понятия сложности алгоритма. Например, понимают под сложностью число проверяемых логических условий. Каждое логическое условие определяет две различные ветки (пути) развития вычислительного процесса. Пусть число всех различных путей в программе есть N. Пусть p_i - вероятность прохождения программы по i-му пути.

Тогда мерой информационной сложности алгоритма (программы) считают энтропию Э, вычисляемую по формуле:

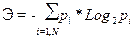
Информационная сложность характеризует возможность п о н я т ь работу алгоритма. Чем больше величина энтропии, тем больше усилий требуется, чтобы разобраться в логике программы. Однако для практики большее значение имеет не информационная, а алгоритмическая или вычислительная сложность алгоритма. Понятие алгоритмической сложности введено советским математиком А.Н.Колмогоровым. Под алгоритмической сложностью он понимал минимально необходимый размер программы для данного алгоритма. Колмогоров полагал, что чем меньше размер записи программы, тем меньше ее сложность. На этом пути ему и его коллегам удалось получить ряд ценных результатов. Вместе с тем оказывается, что даже небольшие по длине записи программы могут требовать огромного времени счета на ЭВМ и это время катастрофически растет с ростом размера входных данных.

Таким образом, выявляется необходимость ввести иную концепцию сложности – вычислительную сложность задачи и связать вычислительную сложность задачи с числом тактов, затрачиваемых машиной Тьюринга, реализующей алгоритм решения этой задачи за кратчайшее возможное число ходов.

Р.Карп обнаружил, что все задачи условно можно разделить на хорошо решаемые (эффективно решаемые) и плохо решаемые (неэффективно решаемые). Разберемся в том, что такое хорошо решаемая задача и эффективный алгоритм. Рассмотрим в качестве примера задачу сортировки следующего массива чисел:

4, 8, 10, 3, 6,9,5,12.

Здесь всего 8 чисел. Один из возможных алгоритмов решения этой задачи состоит в следующем. Сначала найдем наименьшее число и поставим его на первое место. Затем найдем из оставшихся чисел следующее наименьшее число и поставим его на второе место и т.д.

Нетрудно сообразить, что для нахождения наименьшего числа из N чисел следует выполнить N-1 сравнение. Общее число сравнений, которые должен реализовать алгоритм, таким образом, составит

(N-1) + (N-2) + (N-3) + (N-4) + …. +1 = N*N- (1+2+3+…+N-1)=N*N-N*(N-1)/2=

=N*(N-1)/2.

Мы видим, что сложность алгоритма оценивается в этом случае п о л и н о м о м (многочленом, в данном случае второй степени) от числа исходных элементов. В разбираемом нами примере потребовалось бы выполнить 28 сравнений. Р.Карп назвал все алгоритмы, которые требуют полином шагов от размера задачи эффективными или полиномиальными.

Однако есть задачи и алгоритмы вычислительная сложность которых растет быстрее любого полинома. Такие задачи называют плохо решаемыми, а алгоритмы неэффективными.

Рассмотрим следующий пример. Дано слово

НОИКДПОНОК

Буквы в слове переставлены. Нужно определить, какое же слово здесь написано. Пусть наш алгоритм п е р е б и р а е т рутинным способом все возможные варианты и отыскивает полученное слово в словаре русского языка. Из математики известно, что число всех переборов из N элементов составляет N*(N-1)*(N-2)*…*2*1= N! (читается N факториал). В среднем придется сделать половину всех переборов, т.е. 0.58N! Это число для нашего слова все равно очень велико (между прочим, написано - подоконник) и составляет 1714400. Из математики опять-таки известно, что N! растет быстрее любого полинома от N и характер этого роста следует считать лавинообразным.

Для многих практически важных задач, к сожалению, не удается найти хороших алгоритмов, а неэффективные алгоритмы не имеют практической значимости.

Для построения классов вычислительной сложности рассматриваются задачи распознавания, требующие ответа ДА-НЕТ. С таким задачами мы уже встречались выше. Кроме того, для всех таких задач должен быть хороший алгоритм проверки решения.

ОПРЕДЕЛЕНИЕ.Класс задач распознавания типа ДА-НЕТ с хорошим алгоритмом проверки решения называется классом NP (nondeterministic polynomial).

Нам надо объяснить, почему здесь фигурирует слова nondeterministic polynomial (недетерминированный полиномиальный). Речь идет о том, что все такие задачи можно решить за полиномиальное время на н е д е т е р м и н и р о в а н н о й машине Тьюринга. В самом деле, рассмотрим нашу задачу об угадывании слова. Пусть в общем случае слово состоит из N>2 букв. Тогда имеется N правил для выбора позиции для первой буквы, N правил для выбора позиции второй буквы, N правил для выбора позиции третьей буквы и т.д., всего N² правил. Однако имеется одно единственное вычисление, использующее ровно N правил, дающее правильный ответ. Это, разумеется, полиномиальное по сложности вычисление.

Итак, класс NP нами определен. В этом классе есть хорошие и плохие задачи. Подкласс хроших задач в NP называется классом P (polynomial). Подкласс плохих - вссе остальные. Гипотеза мирового значения, которая все еще не доказана, записывается как P=NP (?). Об этой гипотезе и связанной с ней проблемах мы будем говорить далее.