ЛЕКЦИЯ 2. МАШИНЫ ТЬЮРИНГА

Алгоритм является точным математическим понятием. В качестве формальной модели алгоритма исторически первой была модель машины, предложенная англичанином Аланом Тьюрингом в 40-х годах 20-го века. Именно машины Тьюринга получили наибольшее распространение в теоретической математике при изучении свойств алгоритмов. Прежде всего, машины Тьюринга позволили решить многие важные вопросы, связанные с проблемой алгоритмической разрешимости или неразрешимости той или иной проблемы. К этому вопросу мы обратимся несколько ниже.

Машина Тьюринга представляет собой устройство,содержащее пишущую ленту бесконечной длины, разбитую на ячейки Я1, Я2, …, Яn,… . В каждой ячейке может быть записан один и только один символ из входного алфавита машины Тьюринга. В дальнейшем для простоты будем рассматривать алфавит, состоящий всего из двух символов: 0 и 1. При этом также рассматривается пустой “символ” (именно так следует понимать содержимое ячейки, в которой не записан ни 0, ни 1). Пустой символ обычно обозначают как e. В начальный момент на ленту записывается какое-то слово. Обычно это слово представляет собой описание некоторой задачи, на которых специализируется данная машина Тьюринга. Кроме ленты, у машины имеется читающая-пишущая головка, которая позволяется считать символ из ячейки или записать в ячейку, непосредственно находящуюся под головкой, какой-то один символ. Машина Тьюринга работает по тактам. Такты машины Тьюринга никак не привязываются к единицам времени, например, секундам. Но именно в тактах измеряется “время”, затрачиваемое машиной Тьюринга на то, чтобы выполнить обработку входного слова. Разумно и сложность задачи связывать с числом тактов, которую необходимо затратить на Машине Тьюринга для ее решения.

Машина Тьюринга работает по определенным правилам. По своей сути такие правила однотипны и сводятся к следующему: считать символ из текущей ячейки. По текущему состоянию машины и считанному символу определить новое состояние, в которое переходит машина, записать в ячейку новый символ и либо сдвинуть ленту на одну ячейку влево, либо сдвинуть ленту на одну ячейку вправо, либо оставить ленту в прежнем положении, после чего перейти к следующему такту. Машина завершает работу, если она попадает в конечное состояние. Такие правила удобнее всего представлять в виде таблицы. Возьмем в качестве примера следующую таблицу.

В этой таблице использованы следующие обозначения. Состояния машины Тьюринга обозначены как Q₀ , Q₁. Обычно начальное состояние обозначается как Q₀ (и у нас также начальное состояние машины есть Q₀). Состояние Q₁ в нашем примере есть конечное состояние. В верхней строке записаны символы входного алфавита машины. Таких символов три: 0, 1, e. Пустой символ тоже считается символом, хотя реально не соответствует никакому символу вообще.

Рассмотрим строку Q₀. Пусть в текущей ячейке записан 0. На пересечении столбца “0” и строки Q₀ стоит действие машины - eLQ₀. Это действие следует понимать таким образом: первый символ U означает ничего в ячейку не писать. Второй символ L означает сдвинуть ленту на одну ячейку влево (вперед, иначе говоря). Третий символ Q₀ означает, в какое состояние машина переходит (в нашем случае машина остается в старом состоянии, ячейку не изменяет и сдвигает ленту вперед). Рассмотрим теперь столбец 1. Действие теперь таково 0LQ₀. По этому действию в текущую ячейку будет записан 0 вместо 1; все остальное – как и в предыдущем примере. Наконец, последнее действие: UUQ₁. Это действие надо понимать так: ничего в ячейку не писать (первое U), ленту не сдвигать (второе U), перейти в конечное состояние Q₁ . Вот, собственно, и все. Теперь можно догадаться, что представленная выше машина Тьюринга обнуляетчисла, т.е. просто заменяет 1 на 0. Конечно, это - очень элементарная машина. Но надо сразу оговориться, что решать реальные задачи на машине Тьюринга никто не будет. Машина Тьюринга используется для анализа алгоритмов. Например, вопрос типа :”Можно ли решить эту задачу?” есть по сути вопрос “Можно ли для этой задачи построить машину Тьюринга?”

Нумерация машин Тьюринга и универсальная машина Тьюринга.

Для формального анализа различных проблем, связанных с машинами Тьюринга, удобно каждой машине присвоить числовой номер – целое положительное число. Такую нумерацию можно задать разными способами. Одним из известных способов является способ К.Геделя – австрийского математика, доказавшего несколько знаменитых теорем в области логики, теории множеств и теории вычислений. Способ Геделя основан на том, что, как известно из арифметики, любое целое положительное число A можно единственным способом представить в виде произведения простых множителей в виде:

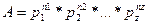
Здесь 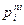- i-й простой множитель числа А; ni – степень, с которой данный множитель входит в разложение числа А. Пример

126=2¹ * 3² *7¹.

Ясно, что порядок множителей в разложении числа значения не имеет. Теперь посмотрим, как получить геделевский номер машины Тьюринга. Такая машина задана своими правилами. Каждое правило можно представить как строку символов

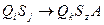
Мы уже знаем, как читать такую строку: если машина находится в состоянии Q_i и читает символ S_j, то она переходит в состояние Q_k , записывает символ S_z вместо S_j и выполняет действие A={оставить ленту на месте; сдвинуть ленту влево на одну ячейку; сдвинуть ленту вправо на одну ячейку}. Получим геделев номер этого правила, используя номера символов в алфавите. Например, пусть используются только заглавные буквы. Каждая буква имеет свой номер: A(1),B(2),C(3),D(4),E(5),F(6),G(7),H(8),I(9),J(10),Q(11),K(12),L(13),M(14),N(15),O(16),P(17),R(18),S(19),T(20),U(21),W(22),X(23),Y(24),Z(25),®(26),0(27),1(28),2(29),3(30),4(31),5(32),6(33),7(34),8(35),9(36),0(37).

Например, правило вида 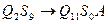дает последовательность чисел: 11,29,19,36,26,11,28,28,19,27,1. Это правило можно заменить однозначным образом на число

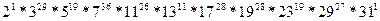
Несмотря на гигантский размер этого числа, нам достаточно знать, как его получить и как по числу восстановить запись правила.

Таким образом, можно получить геделевы номера для правил машины Тьюринга. Теперь расположим эти номера по возрастанию. Пусть при этом получена последовательность чисел 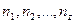. Для этой последовательности чисел снова определяем ее геделев номер. Таким образом, окончательно получим геделев номер машины Тьюринга. Рассмотрим пару чисел 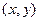. Здесь x – Геделев номер машины Тьюринга, y – произвольное двоичное число на входе машины Тьюринга. Такую пару чисел можно рассматривать как функцию 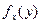, вычисляемую следующим образом. По номеру х определяется набор правил машины Тьюринга. Если х дает синтаксически некорректную спецификацию (неверную запись для правил), то проверяем последовательно номера х+1, х+2, и т.д., пока не получим правильную запись правил. Используя правила полученной машины Тьюринга моделируем ее работу на входе у. В результате, если машина остановится, получим записанное на ленте слово, которое и будем рассматривать, как значение функции 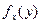. Ясно, что функция 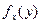может не завершить вычисление за конечное время. Тогда говорим, что ее значение на входе у не определено.

Определение. Класс всех одноместных функций 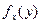, для каждой из которых имеется вычисляющая ее машина Тьюринга, называется классом вычислимых функций.

Теорема. Имеется функция, не являющаяся вычислимой.

Доказательство. Доказательство проводится методом, предложенным Кантором и называется канторовскимдиагональным методом.

Прежде всего, каждую функцию можно рассматривать как отображение одного множества чисел на другое (или на это же множество). Первое множество называется областью определения функции, а второе – областью значений. Мы будем рассматривать только такие функции, у которых область определения и область значений суть множество натуральных чисел. Например, рассмотрим функцию 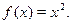Область определения этой функции есть натуральный ряд 1,2,3,…, …. . Натуральный ряд удобно обозначить буквой À, а отображение, реализуемое функцией, в виде À®À. Множество значений также принадлежит этому ряду (хотя и не все числа натурального ряда дают эти значения). Вычислимая функция определяет вычисляемое на машине Тьюринга отображение. Номер вычислимой функции можно связать с номером машины Тьюринга, которая эту функцию вычисляет. Запись 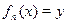можно теперь читать таким образом:

вычислимая функция с номером n отображает число x в число y.

Важно заметить, что вычислимые функции не обязательно всюду определены. Например, у нас есть функция отыскания корня квадратного. Однако нет целого корня, например, у 23 или 47. Следовательно, на этих числах в рассматриваемом нами классе функций от натуральных аргументов данная функция не определена. Однако для этой функции есть машина Тьюринга, т.е. ее правильно назвать частично-вычислимой.

Пусть задан пересчет частично вычислимых функций (вычислимых отображений)

, , ,…, ,….

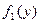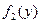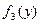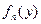Рассмотрим следующую таблицу:

				…
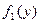
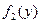
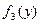
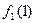	+1
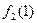
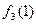
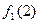
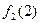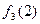
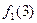
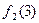
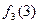		+1
			+1
…
k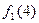
…

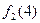
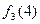
На основании данной таблицы определим следующую функцию

j(x,y)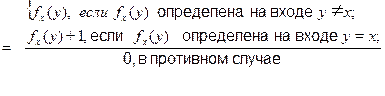

Ясно, что наша новая функция отличается от каждой вычислимой функции 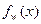в точке x=w и является всюду определенной. Покажем теперь формально, что наша функция j(х,у) не может быть вычислимой никакой машиной Тьюринга. Допустим, что это не так и машина с номером z вычисляет нашу функцию. На основании этой машины можно построить машину для вычисления j(х,x) Тогда получим что j(x,x) = 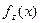. Но это противоречит определению j(х,у) при x=y. Поскольку j(х,x) определена для всех x , то j(z,z) = 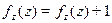, чего быть не может.

Теорема. Для любых целых положительных чисел А и В взаимно однозначно определяется число

С=0.5*((А+В)² +3А+В)

Теорема. Число невычислимых функций несчетно.

Эта теорема доказывается с привлечением знаний из теории множеств. Число всех вычислимых функций счетно, т.к. им соответствуют уникальные номера из натурального ряда чисел. Сколько же всего функций? Каждая функция задает отображение из множества натуральных чисел À в множество натуральных чисел À. При этом если рассматривать всюду определенные тотальные отображения, то 1 можно отобразить в любое из çÀç чисел, далее 2 можно отобразить в любое из çÀç чисел, и .т.д, т.е. всех мыслимых отображений çÀç^çÀç . В теории множеств доказывается, что 2^çÀç >çÀç, что и дает несчетность числа всех определенных отображений (функций).

Литература.

1. З.В.Алферова. Теория алгоритмов. М., Статистика, 1973, 168с.

2. Х.Роджерс. Теория рекурсивных функция и эффективная вычислимость. М., Мир, 1972.

3. М.Гросс, А.Лантен. Теория формальных грамматик. М., Мир, 1971.