ЛЕКЦИЯ 4. РЕКУРСИВНЫЕ МНОЖЕСТВА И ФУНКЦИИ

Как уже было сказано, наряду с определением алгоритма через машину Тьюринга, разрабатывался подход к определению вычислимости через построение функций из простейших (первичных) функций. Этот подход реализовывался С.Клини, А. Черчем и К.Геделем. Понятие рекурсивной функции введено из следующих соображений. Некоторые функции объявляются первичными. Первичную функцию нельзя заменить вычислением более простых функций. Из этих первичных функций строится с помощью определенных операций все множество известных нам вычислимых функций. Таких первичных функций над целыми положительными числами всего три.

А). Функция константа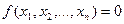

Б) Функция непосредственного следования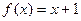

В) Тождественная функция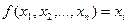

Для построения более сложных функций из первичных используют следующие операции.

· Операция подстановки. Эта операция заключается в том, что вместо каких-то переменных функции подставляют другие функции от тех же или иных переменных.

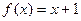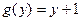Пример. Пусть и . Тогда подставив вместо переменной х функцию g(у), получим новую функцию: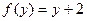

· Операция примитивной рекурсии. Эту операцию можно представить следующим образом

Пример 1. Пусть 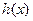- известная вычислимая функция, т.е. известен алгоритм вычисления этой функции для произвольного х. Определим новую функцию f(x) следующим образом:

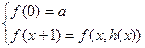
Это и есть определение функции с помощью операции примитивной рекурсии.

Например, пусть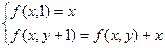

Это есть определение целочисленного умножения. Так

f(3,3)=f(3,2)+3=f(3,1)+3+3=3+3+3=9.

Пример 2. 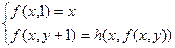и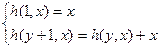

Это определение позволяет находить значение 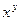. В самом деле, рассмотрим следующий пример вычисления 3² .

f(3,1+1)=h(3,f(3,1))=h(3,3)=h(2+1,3)=h(2,3)+3=h(1+1,3)+3=h(1,3)+3+3=3+3+3=9

Определение. Функция, определяемая из простейших с помощью операций подстановки и/или примитивной рекурсии, называется примитивно рекурсивной.

Имеется еще одна операция для построения рекурсивных функций. Правда, эта операция не всегда дает результат или, как говорят, не является полностью определенной (тотальной). Эта операция называется операцией минимизации (взятия минимального корня). Ее определение таково.

·

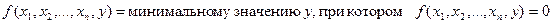
Эту операции можно для простоты обозначить как m_y f(x,y).

Пример 3. Пусть 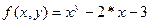. Тогда m_y f(3,y)=2.

Определение. Функция, определяемая из простейших с помощью операций подстановки примитивной рекурсии и минимизации, называется частично рекурсивной.

Имеет место следующая знаменитая гипотеза, известная как Тезис А.Черча

Тезис Черча. Класс всех частично вычислимых функций над положительными целыми числами совпадает с классом всех частично рекурсивных функций.

Иными словами, каждая арифметическая функция, для которой имеется машина Тьюринга, является одновременно и рекурсивной, и наоборот – если функция является частично-рекурсивной, то она одновременно и вычислима.

С помощью тезиса Черча можно устанавливать вычислимость новых функций, используя уже построенные вычислимые функции. Поэтому, если f_x - вычислимая функция с номером x , то h(x)= f_x (x)+1 частично-вычислимая функция.

Множество – это некоторая совокупность элементов. Если множество содержит конечное число элементов, то оно называется конечным. Конечные множества можно задавать непосредственным перечислением содержащихся в них элементов. Бесконечные множества задают, как правило, указанием свойства, которым обладают его элементы. Свойства задают с помощью формул.

Формула, с помощью которого определяется множество, называется характеристической формулой этого множества. Например, множество положительных четных чисел можно задать таким образом

М1={ x | x = 2*N}

Множество составных целых положительных чисел можно задать так

М2 = { x | $n≠1$m≠1 (x=m*n)}

Здесь символ $ означает “существует” и называется квантором существования. Наряду с квантором существования, имеется еще квантор всеобщности - ". С помощью квантора всеобщности можно записать характеристическую формулу множества всех простых чисел М3:

М3 = { x | "n≠1 "m≠1 (x ≠m*n)}

Определим множество

M^co={ x | x Ï M}.

Множество M^co называется дополнением множества М.

Определение. Множество называется рекурсивным, если его характеристическая функция общерекурсивна.

Особенностью рекурсивного множества является то, что для любого х можно с помощью алгоритма вычисления характеристической функции данного множества проверить, принадлежит ли ему х или нет. Поскольку существуют не рекурсивные множества, постольку не для всякого множества можно построить алгоритм для выяснения принадлежности к нему произвольного элемента. Любопытными примерами нерекурсивных множеств являются следующие.

Пример 1. Множество разрешимых (т.е. имеющих корни) диофантовых уравнений.

Уравнение общего вида 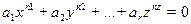где все коэффициенты и переменные целочисленны, называется диофантовым. Советский математик Ю.Матиясевич доказал, что нет алгоритма для решения диофантова уравнения общего вида.

Пример 2. Множество доказуемых формул арифметики целых чисел.

Этот пример известен как теорема К.Геделя о неполноте арифметики целых чисел. Она означает принципиальную недоказуемость некоторых истинных утверждений арифметики. Долгое время считалось, что знаменитая теорема Ферма является примером недоказуемой истинной формулы, пока сравнительно недавно не было получено ее доказательство. Теорема Ферма утверждает, что не существуют такие целые положительные числа a,b,c,n>2, что aⁿ + bⁿ= cⁿ .

Теорема F. Множество MTF финитных самоНЕприменимых машин Тьюринга нерекурсивно.

Будем рассматривать машины Тьюринга с двумя типами конечных состояний, условно называемых “ДА”-состоянием и “НЕТ” –состоянием. Такие машины мы выше определили как распознающие. Говорят, что машина принимает входное слово z, если обработка этого слова заканчивается в состоянии “ДА”. Если же обработка слова z заканчивается в состоянии “НЕТ”, то говорят, что машина отклоняет слово z. Машина может, вообще говоря, зациклиться, но такие машины теорема не рассматривает – речь идет о финитных машинах, т.е. о таких машинах, которые каждое вычисление заканчивают либо в состоянии “НЕТ”, либо в состоянии “ДА”. СамоНЕприменимые машины – это такие машины, которые не принимают свои собственные описания, т.е. при подаче на их вход набора правил этих же машин они заканчивают в состоянии “НЕТ”.Теперь докажем теорему F.

Доказательство. Пусть имеется, вопреки утверждению, машина, вычисляющая характеристическую формулу множества MTF. Обозначим эту машину M_MTF. Это значит, что M_MTF переходит в состояние “ДА” на входе x, где x – набор правил произвольной машины Тьюринга, если машина с данным набором правил не принимает этот набор правил. Спрашивается, в каком состоянии M_MTF закончит вычисление, если на ее вход подать набор правил ее самой? Если она примет этот набор, то это означает, что машина M_MTF самоНЕприменима, т.е. не принимает подобные наборы – противоречие. Если же M_MTF не примет данный набор, то она должна его принять – снова противоречие.

Теорема A. Множество MTA финитных самоприменимых машин Тьюринга нерекурсивно.

Указание. Доказательство можно получить непосредственно из доказательства теоремы F. Нужно показать, что MTA есть дополнение множества MTF. Теперь, если допустить, что MTA рекурсивно, то рекурсивным должно быть и множество MTF , но этого нет.

Определение. Множество A называется рекурсивно перечислимым, если его характеристическая функция f(x) частично рекурсивна, причем

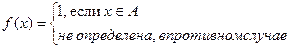
Мы помним, что частичная рекурсивность характеристической функции означает, что значение этой функции для некоторых элементов не известно (машина Тьюринга зацикливается на подобных входах). Однако в случае рекурсивной перечислимости, машина зацикливается тогда и только тогда, когда она пытается распознать элемент не из своего множества.

Литература

1. Н.Катленд. Вычислимость. Введение в теорию рекурсивных функций. М., Мир, 1983.