ЛЕКЦИЯ 5. АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ

Рассмотрим проблему алгоритмической разрешимости (неразрешимости) на некоторых примерах.

Пример 1. Алгоритмическая неразрешимость проблемы самораспознавания.

Набор правил каждой машины Тьюринга можно представить соответствующим геделевским номером. Обозначим М_y - набор правил машины Тьюринга с номером у. Рассмотрим язык L={y_i | машина M 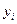отклоняет слово y_i }. Таким образом в язык L войдут номера тех и только тех машин Тьюринга, которые отклоняют свои номера. Спросим, можно ли распознать этот язык ? Ответ отрицательный. В самом деле, если бы такая машина была, то она либо приняла бы свой собственный номер, либо отклонила. Оба эти варианта невозможны в силу определения языка L.

Любопытно заметить, что данная проблема имеет содержательный аналог в лице проблемы о деревенском брадобрее. Последняя формулируется так. В одном селе брадобрей бреет тех и только тех людей, которые не бреются сами. Спрашивается, бреет ли он самого себя?

Ответ не может быть ни положительным, ни отрицательным. Значит, такого брадобрея не существует (брадобрей играет роль машины для распознавания языка L.)

Пример 2. Проблема самоприменимости может быть проиллюстрирована также на следующей задаче.

Каждый, кто в состоянии пройти через лабиринт, называется проводником. В любой момент времени в лабиринте может быть не более двух проводников. Любой проводник Z называется сертифицированным, если и только если он имеет сертификат, который гарантирует, что Z является проводником.

Предположим, некоторый X (и все ему подобные) может пройти через лабиринт, используя любого сертифицированного проводника Y и, по крайней мере, всегда один такой Y отыщется и Y не может отказать X.

Следовательно, Х всегда в состоянии пройти через лабиринт и должен получить сертификат по формальным признакам. Однако, если Х получит сертификат, то при использовании Х-ом другого такого Х, он может не выбраться из лабиринта, поскольку сам по себе Х может не найти путь.

Следовательно, Х нельзя сертифицировать, хотя Х способен пройти через лабиринт.

Рассмотрим теперь машину Тьюринга, моделирующую другие машины Тьюринга, которые являются доказательно финитными на произвольном входе. Чтобы смоделировать другую машину достаточно знать ее правила. Такую машину назовем универсальной и обозначим M_un. На примере о проводнике мы видим, что нельзя доказать, что M_un является финитной машиной, т.е. останавливается на любом входе. Но нельзя доказать, что M_un является не финитной (зацикливается) на каком-нибудь входе, поскольку она моделирует только такие машины, которые сами являются доказательно финитными (читай, сертифицированными пловцами). Следовательно, для M_un нельзя ни доказать, что она финитна, ни опровергнуть это. А по сему, если бы был способ узнать, останавливается ли M_un на любом входе или нет, то мы бы установили финитность или не финитность M_un вопреки недоказуемости этого факта.

Мы получили следующий результат.

Нельзя доказательно построить алгоритм, который устанавливал бы финитность или не финитность других машин Тьюринга на произвольном входе. Этому результату можно придать и формальный вид.

Обозначим через 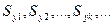перечисление всех областей сходимости машин Тьюринга с номерами y1, y2,…, yk, ….. соответственно.

Сформулируем проблему: можно ли для любого числа x выяснить, xÏ 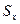? Если бы такой алгоритм W был, то у него был бы некоторый геделев номер, скажем w. Спросим wÏS_w ? Если да, то W должен принять w по определению , что невозможно. Если нет, т.е. wÎS_w, то W сходится на w, а это значит, по условию, что wÏS_w - снова противоречие.

Используя неразрешимость проблемы остановки, покажем, что енельзя построить алгоритм для отыскания корней произвольной вычислимой функции.

Нам потребуется следующий простой результат.

УТВЕРЖДЕНИЕ. Ели функция f(x) вычислима, то вычислима и обратная ей функция.

Доказательство. Пусть M_y - правила машины Тьюринга, которая вычисляет f_y(x).

Возьмем какое-нибудь одно из ее правил, например,

Qi a ® Qj b L

Читаем: если машина находится в состоянии Qi и читает символ a, то она переходит в состояние Qj, записывает вместо a символ b и сдвигает ленту влево.

Перепишем это правило 'в обратную сторону"

Qj b ® Qi a R

Это правило показывает, как работает машина Тьюринга, вычисляющая обратную функцию для данной вычислимой функции. Таким же образом прямо показывается, что любое правило машины Тьюринга можно заменить "обратным", что доказывает УТВЕРЖДЕНИЕ.

Рассмотрим уравнение f_y(x) = с, где c – положительное целое число, например

2*x=4. Здесь f_y(x) =2*x. Обратная функция есть x=0.5*y. Найти корень уравнения 2*x=4 это то же самое, что ответить на вопрос: останавливается ли на входе y=4 машина, вычисляющая обратную функцию. Таким образом, проблема отыскания корня произвольной вычислимой функции на произвольном входе равносильна проблеме останова, а последняя алгоритмически не разрешима.

В заключение обратимся к знаменитому результату К.Геделя.

Теорема К. Геделяо неполноте формальных систем, содержащих арифметику целых чисел. Существуют истинные недоказуемые формулы.

Общая идея доказательства. Пусть формула j(x,y) истинна, если y есть доказательство формулы с номером x. Недоказуемость формулы j(x,y) равносильна формуле "y(Øj(x,y)). По правилам логики последняя формула эквивалентна некоторой формуле l(x), в которой y уже не присутствует. Формула l(x) утверждает недоказуемость формулы с номером x. Пусть e - номер формулы l(x). Тогда l(e) утверждает собственную недоказуемость. Формула l(e) не может быть ложной, поскольку ложные формулы недоказуемы в непротиворечивых системах. Следовательно, она истинна и не доказуема.