Лекция 14. Предмет дискретной математики. Место и роль дискретной математики в системе математических наук и в решении задач, связанных с обеспечением информационной безопасности.
В последние годы инженеры-математики, занимающиеся прикладными исследованиями, все больше используют аппарат дискретной математики. Это объясняется необходимостью создания и эксплуатации современных ЭВМ, средств передачи и обработки информации, автоматизированных систем управления и проектирования.
С прикладной точки зрения интерес к функциям алгебры логики основан на том, что вся современная электроника (в т. ч. компьютерная) – цифровая 0-1 электроника. Успехи, достигнутые в этой области, позволили применять 0-1 электронику и там, где, казалось, должна была вечно господствовать континуальная электроника – в радиовещании и телевидении. Аудио и видеозапись высокого качества, в том числе и системы телевидения высокого разрешения, лазерные проигрыватели и т. п. – это тоже системы 0-1 электроники.
В настоящее время в учебных планах различных инженерных специальностей появилась дисциплина “Дискретная математика“.
Дискретная математика – самостоятельное направление современной математики. Она изучает математические модели объектов, процессов, зависимостей, существующих в реальном мире, с которыми имеют дело в технике, информатике и других областях знаний.
Дискретная математика, или дискретный анализ – область математики, которая занимается исследованием структур и задач на конечных множествах. Поэтому в качестве синонима иногда используется термин «конечная математика». Можно считать общепринятым деление математики на непрерывную и дискретную. Последняя представляет собой важное направление, имеющее характерные для него предмет исследований, методы и задачи. Специфика задач дискретной математики в первую очередь предполагает отказ от основных понятий классической математики – предела и непрерывности. Поэтому для задач дискретной математики обычные средства классического анализа являются вспомогательными.
Дискретная и непрерывная математика взаимно дополняют друг друга. Понятия и методы одной часто используются в другой. Один и тот же объект может рассматриваться с двух точек зрения и в зависимости от этого выбирается непрерывная или дискретная математика.
При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются дискретные методы формализованного представления, являющиеся предметом рассмотрения в дискретной математике. К ним относятся методы, основанные на теоретико-множественных представлениях, графы, алгоритмы, математическая логика и др.
Дискретная математика предлагает:
· универсальные средства (языки) формализованного представления;
· способы корректной переработки информации, представленной на этих языках;
· возможности и условия перехода с одного языка описания явлений на другой с сохранением содержательной ценности моделей.
Сегодня дискретная математика является важным звеном математического образования. Умение проводить анализ, композицию и декомпозицию информационных комплексов и информационных процессов – обязательное квалификационное требование к специалистам в области информатики.
Множество - это одно из основных понятий математики, как дискретной, так и непрерывной. Оно не определяется через другие понятия. Содержательно, под множеством понимается некоторая совокупность элементов. Основное отношение между элементами и множеством - это отношение принадлежности элемента множеству. Оно обозначается знаком 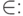
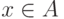 означает, что элемент x принадлежит множеству A.
означает, что элемент x принадлежит множеству A. 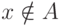 означает, что элемент x не входит в множество A.
означает, что элемент x не входит в множество A. 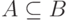 означает, что каждый элемент множества A является также элементом множества B. В этом случае множество A называетсяподмножеством множества B. Если
означает, что каждый элемент множества A является также элементом множества B. В этом случае множество A называетсяподмножеством множества B. Если 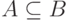 и
и 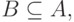 то A=B, т.е. множества A и B равны. Если
то A=B, т.е. множества A и B равны. Если 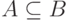 и
и  то A называется собственным подмножеством множества B, и в этом случае пишем
то A называется собственным подмножеством множества B, и в этом случае пишем 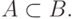 Множество, не содержащее элементов, называется пустым и обозначается
Множество, не содержащее элементов, называется пустым и обозначается  .
.
Обычно множества обозначаются с помощью пары фигурных скобок, в которые заключены их элементы. Небольшие множествазадаются прямым перечислением всех элементов. Например, множество простых чисел, не превосходящих 10, это {2, 3, 5, 7}; множество (имен) летних месяцев: {июнь, июль, август}. В описаниях "больших" конечных множеств используют многоточие. В них часто указывается несколько первых элементов и последний элемент множества. Например, множество целых неотрицательных чисел, не превосходящих 100, записывают как {0, 1, 2, ... , 100}, множество всех месяцев года - как { январь, февраль, ..., декабрь}. Такое задание требует определенной аккуратности. Например, если некоторое множество Aзадано как {3, 5, 7, ... , 19}, то не ясно, является ли A множеством нечетных чисел, лежащих в интервале от 3 до 19, или это множество простых чисел из того же интервала (возможны и другие его расшифровки). Перечисления элементов бесконечных множеств начинаются несколькими начальными элементами, а завершаются многоточием. При этом часто указывают общий вид элемента задаваемого множества. Основное бесконечное множество, рассматриваемое в дискретной математике, этомножество всех натуральных чисел N={1, 2, 3, ... } . Множество всех квадратов этих чисел можно задать, например, так: {1, 4, 9, ..., n2, ... } .
Как мы уже отметили, большие множества не всегда можно точно определить, используя перечисление с многоточием. Основной способ их описания имеет вид: { Elem | условие на Elem}, где Elem - это общий вид элемента определяемого множества, а после вертикальной черты описано условие, которому этот элемент должен удовлетворять. Например,  - это множество целых чисел в интервале от 10 до 1000,
- это множество целых чисел в интервале от 10 до 1000,  - множество квадратов натуральных чисел,
- множество квадратов натуральных чисел,  - множество всех простых чисел.
- множество всех простых чисел.
Множества, элементами которых являются другие множества, часто называют семействами или классами. Семейство ( множество ) всех подмножеств множества A обозначается через 2A, т.е. 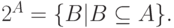 Например, если A={ 0, 1, {2,3}}, то
Например, если A={ 0, 1, {2,3}}, то 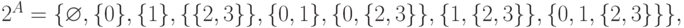 а дляпустого множества
а дляпустого множества  семейство его подмножеств
семейство его подмножеств 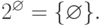
Дата добавления: 2016-06-05; просмотров: 5262;











