Лекция 8. Исследование функции с помощью производной: интервалы монотонности и экстремумы функции. Асимптоты. Исследование функций и построение их графиков.
Необходимое условие возрастания и убывания функции.
Из определений возрастающей и убывающей функций следует необходимое условие возрастания и убывания функции.
Т. Если дифференцируемая функция  возрастает (
возрастает ( 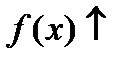 ) на сегменте
) на сегменте 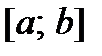 , то
, то 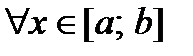 ее первая производная
ее первая производная 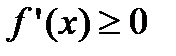 . Если диффе-ренцируемая функция
. Если диффе-ренцируемая функция  (
( 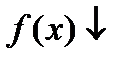 ) убывает на сегменте
) убывает на сегменте 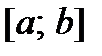 , то
, то 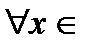
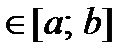 ее первая производная
ее первая производная 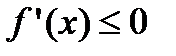 .
.
Док-во. Пусть дифференцируемая функция  возрастает на сегменте
возрастает на сегменте 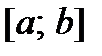 . Возьмем произвольную точку
. Возьмем произвольную точку 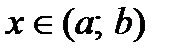 и дадим ей приращение
и дадим ей приращение 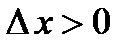 . Тогда в силу возрастания функции ее приращение
. Тогда в силу возрастания функции ее приращение 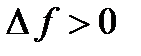 . Отсюда следует, что величина
. Отсюда следует, что величина 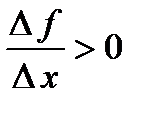 . Совершая предельный переход в этом неравенстве при
. Совершая предельный переход в этом неравенстве при 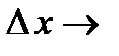
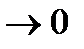 , получим
, получим 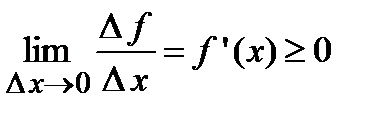 . Аналогично теорема доказывается в случае, когда функция
. Аналогично теорема доказывается в случае, когда функция  убывает на сегменте
убывает на сегменте 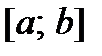 .
.
С геометрической точки зрения возрастающая на сегменте 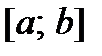 функция
функция  в каждой точке своего графика характеризуется касательной, которая образует с положительным направлением оси абсцисс острый угол. Если функция
в каждой точке своего графика характеризуется касательной, которая образует с положительным направлением оси абсцисс острый угол. Если функция  убывает на сегменте
убывает на сегменте 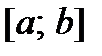 , то касательная образует с положительным направлением оси абсцисс тупой угол.
, то касательная образует с положительным направлением оси абсцисс тупой угол.
Пример Найти интервалы возрастания и убывания функции 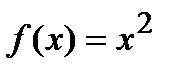 .
.
Из графика этой функции видно, что 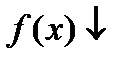
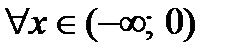 и
и 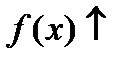
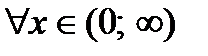 . Согласно необходимому признаку возрастания и убывания функции
. Согласно необходимому признаку возрастания и убывания функции  вычислим ее первую производную:
вычислим ее первую производную: 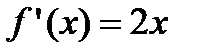 . Эта производная будет отрицательной
. Эта производная будет отрицательной 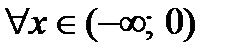 и положительной
и положительной 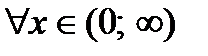 величиной. Следовательно, в полном соответствии с графиком функции
величиной. Следовательно, в полном соответствии с графиком функции 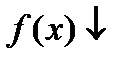
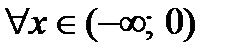 и
и 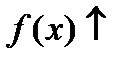
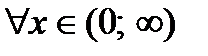 .
.
Достаточное условие возрастания и убывания функции.
Т. Пусть функция  непрерывна на сегменте
непрерывна на сегменте 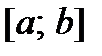 и дифференцируема на интервале
и дифференцируема на интервале 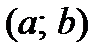 . Если ее первая производная
. Если ее первая производная 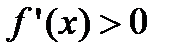
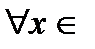
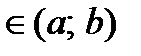 , то функция возрастает на сегменте
, то функция возрастает на сегменте 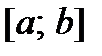 . Если ее первая производная
. Если ее первая производная 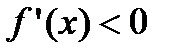
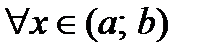 , то функция убывает на сегменте
, то функция убывает на сегменте 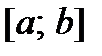 .
.
Док-во. Пусть первая производная функции 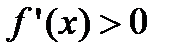
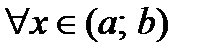 . Возьмем из этого интервала две любые точки
. Возьмем из этого интервала две любые точки 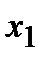 и
и 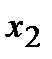 (для определенности примем, что
(для определенности примем, что 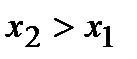 ). Тогда по теореме Лагранжа на интервале
). Тогда по теореме Лагранжа на интервале 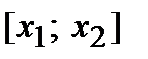 найдется хотя бы одна точка
найдется хотя бы одна точка 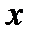 такая, что
такая, что 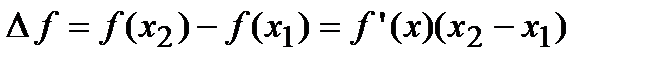 . Так как на интервале
. Так как на интервале 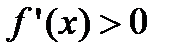
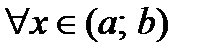 и
и 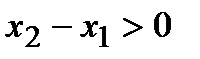 , следовательно,
, следовательно, 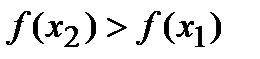 . Таким образом, функция
. Таким образом, функция  возрастает на сегменте
возрастает на сегменте 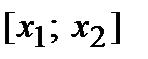 . В силу произвольности выбранных точек
. В силу произвольности выбранных точек 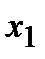 и
и 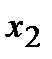 полученное утверждение справедливо для всего сегмента
полученное утверждение справедливо для всего сегмента 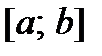 . Достаточное условие убывания функции
. Достаточное условие убывания функции  на сегменте
на сегменте 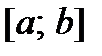 доказать самостоятельно.
доказать самостоятельно.
Условия постоянства функции на сегменте 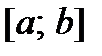 .
.
Т. Пусть функция  непрерывна на сегменте
непрерывна на сегменте 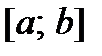 и дифференцируема на интервале
и дифференцируема на интервале 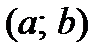 . Если ее первая производная
. Если ее первая производная 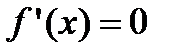
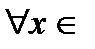
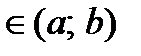 , то функция постоянна на сегменте
, то функция постоянна на сегменте 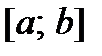 .
.
Док-во. Пусть первая производная функции 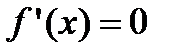
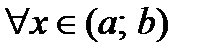 . Возьмем произвольную точку
. Возьмем произвольную точку 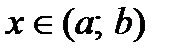 и рассмотрим сегмент
и рассмотрим сегмент 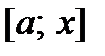 . На этом сегменте выполняются все условия теоремы Лагранжа, следовательно,
. На этом сегменте выполняются все условия теоремы Лагранжа, следовательно, 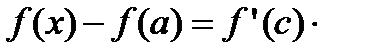
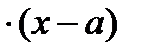 , где
, где 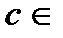
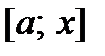 . Так как по условию теоремы
. Так как по условию теоремы 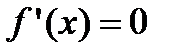
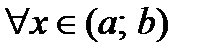 , то и точке
, то и точке  первая производная функции обращается в ноль. Отсюда получаем, что
первая производная функции обращается в ноль. Отсюда получаем, что 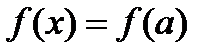 . В силу произвольности точки
. В силу произвольности точки 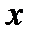 полученное равенство выполняется
полученное равенство выполняется 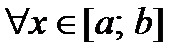 , т.е. функция постоянна на сегменте
, т.е. функция постоянна на сегменте 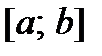 .
.
Минимум и максимум (экстремумы) функции.
Пусть функция  непрерывна в точке
непрерывна в точке 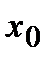 .
.
Опр. Функция  имеет в точке
имеет в точке 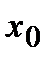 минимум (
минимум (  ), если существует такая
), если существует такая 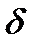 -окрестность точки
-окрестность точки 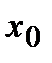 , что
, что 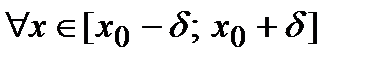 значение функции в любой другой точке
значение функции в любой другой точке 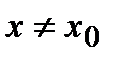 из
из 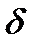 -окрестность точки
-окрестность точки 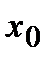 превышает значение функции в самой точке
превышает значение функции в самой точке 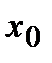 , т.е. выполняется неравенство
, т.е. выполняется неравенство 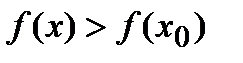 .
.
Обозначение 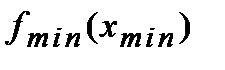 .
.
Опр. Функция  имеет в точке
имеет в точке 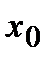 максимум (
максимум ( 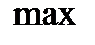 ), если существует такая
), если существует такая 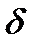 -окрестность точки
-окрестность точки 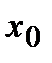 , что
, что 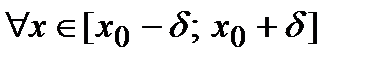 значение функции в любой другой точке
значение функции в любой другой точке 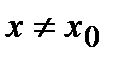 из
из 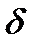 -окрестность точки
-окрестность точки 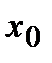 меньше значения функции в самой точке
меньше значения функции в самой точке 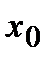 , т.е. выполняется неравенство
, т.е. выполняется неравенство 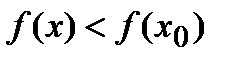 .
.
Обозначение 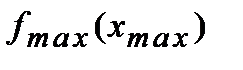 .
.
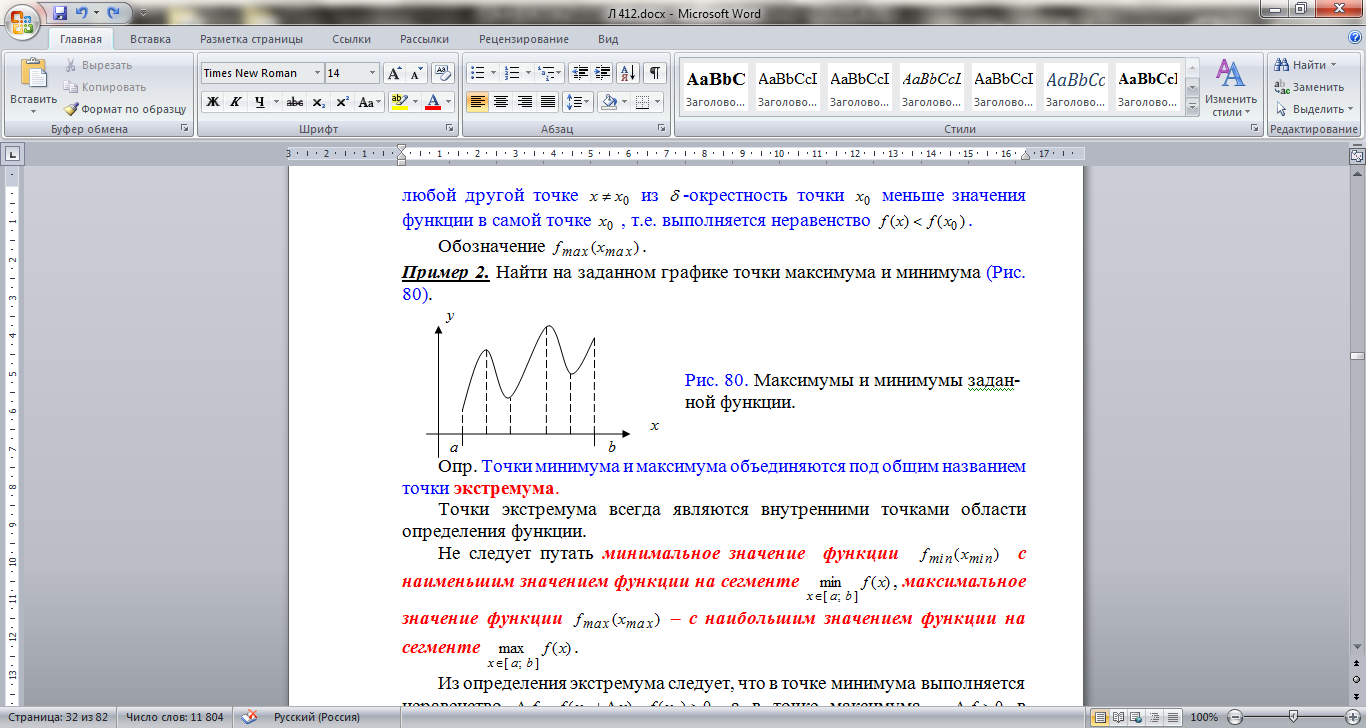 Пример Найти на заданном графике точки максимума и минимума на рисунке.
Пример Найти на заданном графике точки максимума и минимума на рисунке.
Опр. Точки минимума и максимума объединяются под общим названием точки экстремума.
Точки экстремума всегда являются внутренними точками области определения функции.
Не следует путать минимальное значение функции 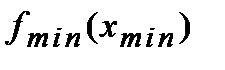 с наименьшим значением функции на сегменте
с наименьшим значением функции на сегменте 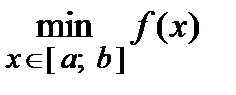 , максимальное значение функции
, максимальное значение функции 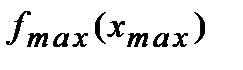 – с наибольшим значением функции на сегменте
– с наибольшим значением функции на сегменте 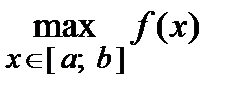 .
.
Из определения экстремума следует, что в точке минимума выполняется неравенство 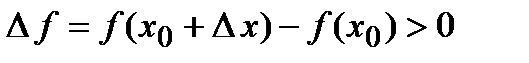 , а в точке максимума –
, а в точке максимума – 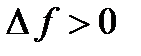 в некоторой малой
в некоторой малой 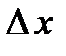 -окрестности точки
-окрестности точки 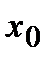 .
.
Необходимое условие существования экстремума функции.
Т4. Если дифференцируемая функция  имеет в точке
имеет в точке 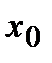 экстремум, то ее первая производная в этой точке равна нулю, т.е.
экстремум, то ее первая производная в этой точке равна нулю, т.е. 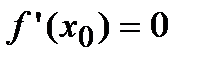 .
.
Док-во. Пусть в точке 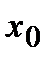 функция
функция  имеет максимум. Так как функция
имеет максимум. Так как функция  дифференцируема в точке
дифференцируема в точке 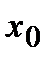 , то в этой точке существует ее первая производная
, то в этой точке существует ее первая производная 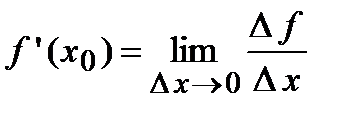 . При стремлении
. При стремлении 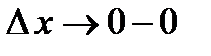 (слева) приращение аргумента
(слева) приращение аргумента 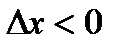 , а приращение функции
, а приращение функции 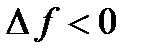 , следовательно,
, следовательно, 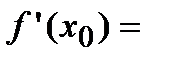
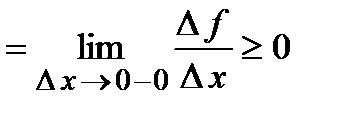 . При стремлении
. При стремлении 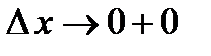 (справа) приращение аргумента
(справа) приращение аргумента 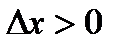 , а приращение функции
, а приращение функции 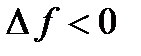 , следовательно,
, следовательно, 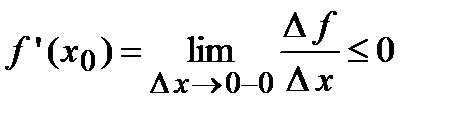 .
.
Так как производная в точке 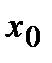 не может одновременно быть и отрицательной и положительной, то в этой точке она равна нулю, т.е.
не может одновременно быть и отрицательной и положительной, то в этой точке она равна нулю, т.е. 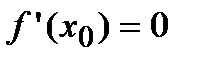 . Случай, когда в точке
. Случай, когда в точке 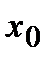 наблюдается минимум, доказать самостоятельно.
наблюдается минимум, доказать самостоятельно.
Обращение в нуль первой производной функции в точке 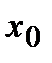 является необходимым, но не достаточным условием существования экстремума в этой точке. Непрерывная функция может иметь экстремум в точке
является необходимым, но не достаточным условием существования экстремума в этой точке. Непрерывная функция может иметь экстремум в точке 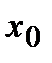 даже в том случае, когда ее первая производная в этой точке не существует. В этом случае говорят об “острых” экстремумах.
даже в том случае, когда ее первая производная в этой точке не существует. В этом случае говорят об “острых” экстремумах.
Опр. Точки, в которых первая производная функции обращается в нуль или не существует, называются критическими (стационарными или подозрительными на экстремум).
Всякая точка экстремума является критической точкой, однако не любая критическая точка будет экстремумом.
Пример Доказать, что функция 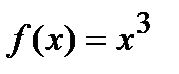 не имеет экстремума в точке
не имеет экстремума в точке 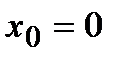 .
.
В точке 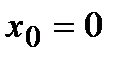 первая производная функции
первая производная функции 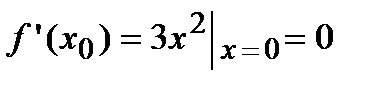 . Однако из графика кубической параболы видно, что в точке
. Однако из графика кубической параболы видно, что в точке 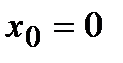 она экстремума не имеет. Следовательно, исследуемая точка является критической точкой, но не точкой экстремума.
она экстремума не имеет. Следовательно, исследуемая точка является критической точкой, но не точкой экстремума.
Первый и второй достаточные признаки существования экстремума.
Первый достаточный признак существования экстремума дается теоремой:
Т1. Если функция  дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки 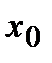 , кроме может быть самой точки
, кроме может быть самой точки 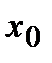 , и при переходе через эту точку слева направо ее первая производная меняет свой знак с “+” на “–”, то в точке
, и при переходе через эту точку слева направо ее первая производная меняет свой знак с “+” на “–”, то в точке 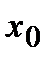 функция
функция  имеет максимум, а если ее первая производная меняет свой знак с “–” на “+”, то в точке
имеет максимум, а если ее первая производная меняет свой знак с “–” на “+”, то в точке 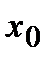 функция
функция  имеет минимум. Если при переходе через точку
имеет минимум. Если при переходе через точку 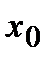 первая производная не меняет свой знак, то в этой точке экстремума нет.
первая производная не меняет свой знак, то в этой точке экстремума нет.
Второй достаточный признак существования экстремума дается теоремой:
Т2. Если в точке 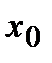 первая производная функци
первая производная функци  обращается в ноль (
обращается в ноль ( 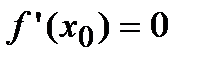 ), а вторая производная существует, непрерывна в некоторой окрестности этой точки и отлична от нуля в самой точке (
), а вторая производная существует, непрерывна в некоторой окрестности этой точки и отлична от нуля в самой точке ( 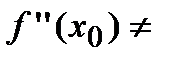
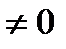 ), то в точке
), то в точке 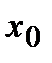 наблюдается экстремум. Если при этом
наблюдается экстремум. Если при этом 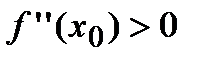 , то точка
, то точка 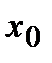 является точкой минимума, а при
является точкой минимума, а при 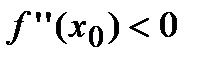 – точкой максимума.
– точкой максимума.
Пример. Найти и определить тип экстремумов функции 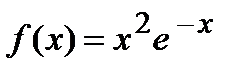 .
.
Вычислим первую производную функции и приравняем ее к нулю с целью отыскания критических точек: 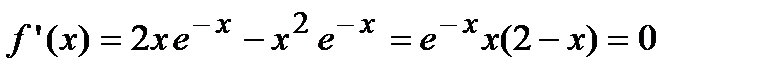 . Так как показательная функция
. Так как показательная функция 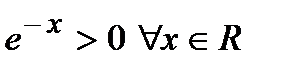 , то
, то 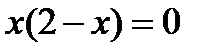 . Отсюда находим критические точки
. Отсюда находим критические точки 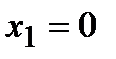 и
и 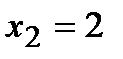 . Отложим эти точки на числовой оси и на каждом интервале определим знак первой производной функции, т.е. применим первый достаточный признак существования экстремума:
. Отложим эти точки на числовой оси и на каждом интервале определим знак первой производной функции, т.е. применим первый достаточный признак существования экстремума: 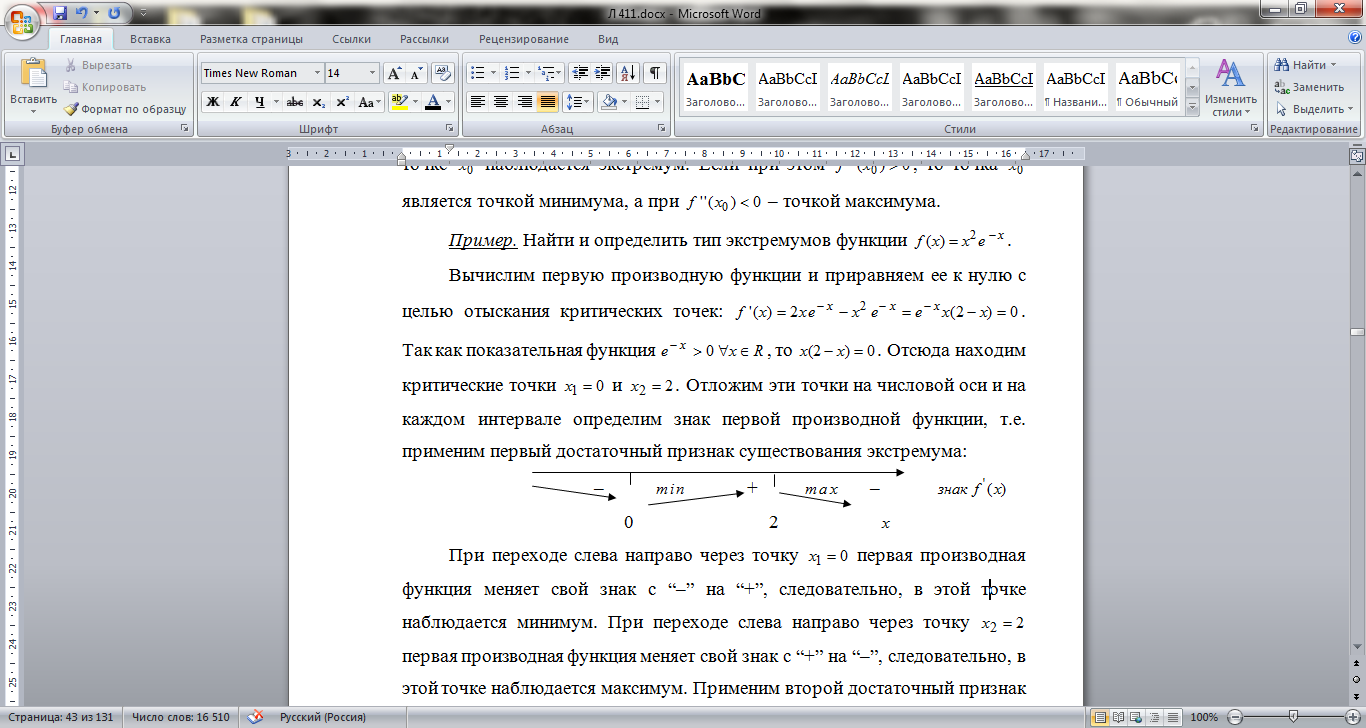
При переходе слева направо через точку 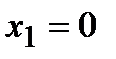 первая производная функция меняет свой знак с “–” на “+”, следовательно, в этой точке наблюдается минимум. При переходе слева направо через точку
первая производная функция меняет свой знак с “–” на “+”, следовательно, в этой точке наблюдается минимум. При переходе слева направо через точку 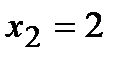 первая производная функция меняет свой знак с “+” на “–”, следовательно, в этой точке наблюдается максимум. Применим второй достаточный признак существования экстремума, для чего вычислим вторую производную функции:
первая производная функция меняет свой знак с “+” на “–”, следовательно, в этой точке наблюдается максимум. Применим второй достаточный признак существования экстремума, для чего вычислим вторую производную функции: 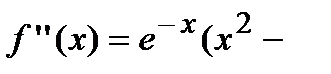
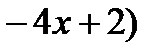 . Вычислим значение второй производной функции в точке
. Вычислим значение второй производной функции в точке 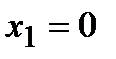 :
: 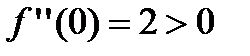 , следовательно, в этой точке функция имеет минимум. Вычислим значение второй производной функции в точке
, следовательно, в этой точке функция имеет минимум. Вычислим значение второй производной функции в точке 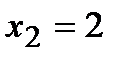 :
: 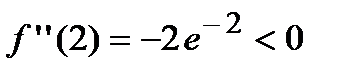 , следовательно, в этой точке функция имеет максимум.
, следовательно, в этой точке функция имеет максимум.
Наименьшее и наибольшее значения функции на сегменте 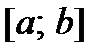 .
.
Пусть функция  непрерывна на сегменте
непрерывна на сегменте 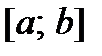 и имеет конечное число точек экстремума на этом интервале. Если наибольшее значение функция достигает внутри сегмента, то очевидно, что это будет один из максимумов (аналогично для наименьшего значения – один из минимумов). Однако возможны варианты, когда функция достигает своих наименьшего и наибольшего значений на концах заданного сегмента. Поэтому для отыскания этих значений применяют следующую схему:
и имеет конечное число точек экстремума на этом интервале. Если наибольшее значение функция достигает внутри сегмента, то очевидно, что это будет один из максимумов (аналогично для наименьшего значения – один из минимумов). Однако возможны варианты, когда функция достигает своих наименьшего и наибольшего значений на концах заданного сегмента. Поэтому для отыскания этих значений применяют следующую схему:
1. Находят область определения функции и убеждаются в том, что заданный сегмент входит в эту область.
2. Находят критические точки, для чего решают уравнение 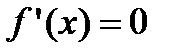 , и точки, в которых первая производная функции не существует.
, и точки, в которых первая производная функции не существует.
3. Вычисляют значения функции в критических точках, принадлежащих заданному сегменту, в точках, в которых первая производная функции не существует и на концах заданного сегмента.
4. Из полученных чисел выбирают наименьшее 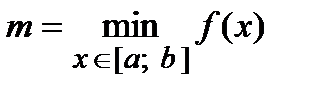 и наибольшее
и наибольшее 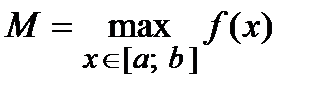 .
.
Пример Найти наименьшее и наибольшее значения функции 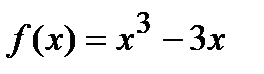 на сегменте
на сегменте 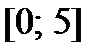 .
.
Действуя согласно вышеприведенной схеме, находим:
1. 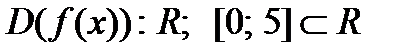 . Следовательно, функция определена и непрерывна на заданном сегменте.
. Следовательно, функция определена и непрерывна на заданном сегменте.
2. Вычислим первую производную 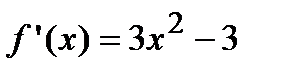 . Производная существует на всей числовой оси, поэтому найдем критические точки
. Производная существует на всей числовой оси, поэтому найдем критические точки 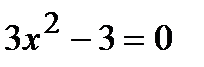 . Отсюда находим, что
. Отсюда находим, что 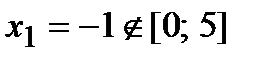 и
и 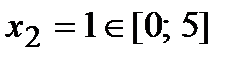 .
.
3. Вычислим значение функции в критических точках и на концах заданного сегмента: 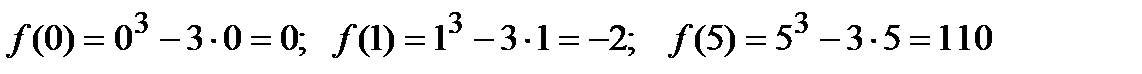 .
.
4. Из полученных чисел выбираем наименьшее 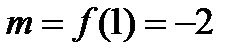 и наибольшее
и наибольшее 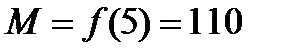 , которые определяют наименьшее и наибольшее значения функции
, которые определяют наименьшее и наибольшее значения функции 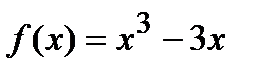 на сегменте
на сегменте 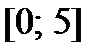 .
.
Выпуклость и вогнутость графика функции. Точки перегиба.
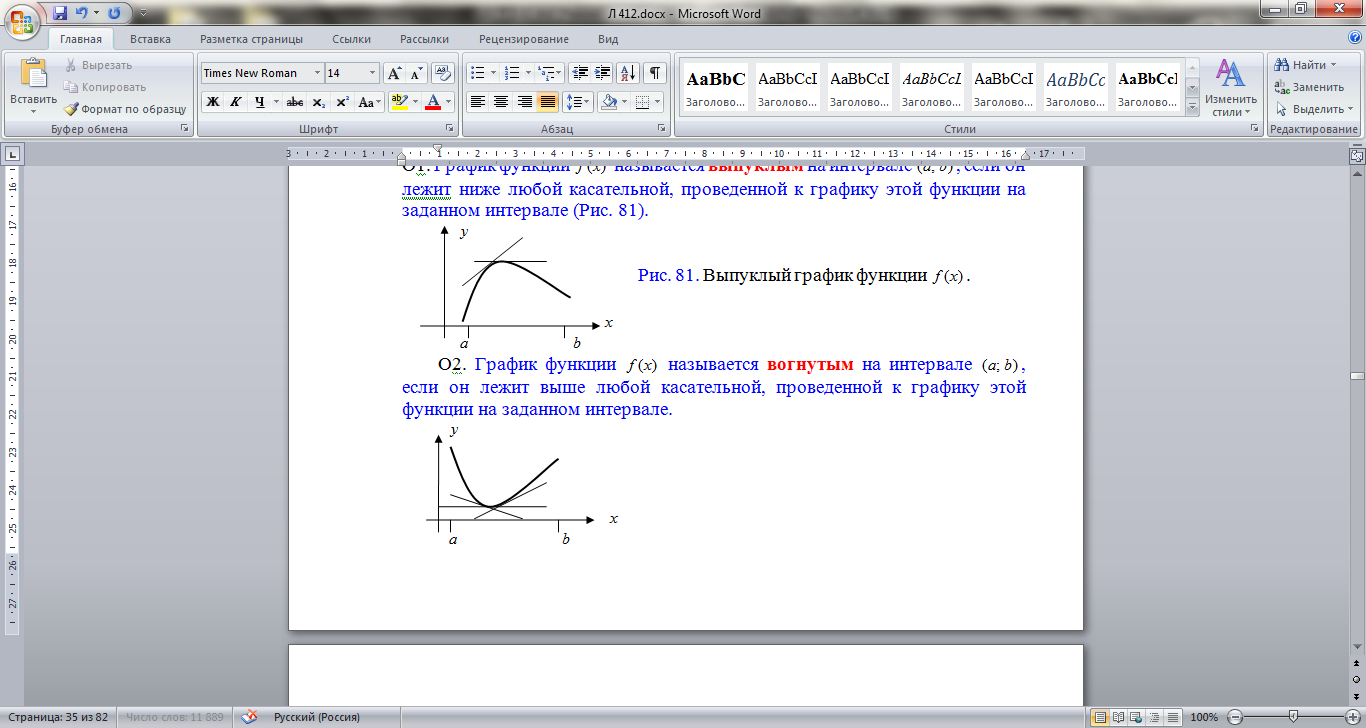 Опр. График функции
Опр. График функции  называется выпуклым на интервале
называется выпуклым на интервале 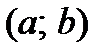 , если он лежит ниже любой касательной, проведенной к графику этой функции на заданном интервале.
, если он лежит ниже любой касательной, проведенной к графику этой функции на заданном интервале.
Опр. График функции  называется вогнутым на интервале
называется вогнутым на интервале 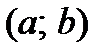 , если он лежит выше любой касательной, проведенной к графику этой функции на заданном интервале.
, если он лежит выше любой касательной, проведенной к графику этой функции на заданном интервале.
 Достаточные условия выпуклости и вогнутости графика функции на том или ином интервале определяются теоремой:
Достаточные условия выпуклости и вогнутости графика функции на том или ином интервале определяются теоремой:
Т3. Если вторая производная функции  на интервале
на интервале 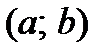 существует и положительна, то на этом интервале график функции
существует и положительна, то на этом интервале график функции  будет вогнутым. Если вторая производная функции
будет вогнутым. Если вторая производная функции  на интервале
на интервале 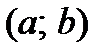 существует и отрицательна, то на этом интервале график функции
существует и отрицательна, то на этом интервале график функции  будет выпуклым.
будет выпуклым.
Пример Определить интервалы вогнутости и выпуклости графика функции 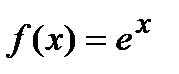 .
.
Найдем вторую производную от заданной функции 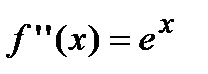 . В силу того, что
. В силу того, что 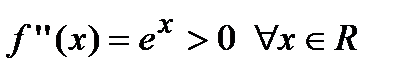 , то график функции
, то график функции 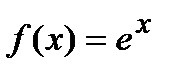 будет вогнутым на всей числовой оси.
будет вогнутым на всей числовой оси.
Пример Определить интервалы вогнутости и выпуклости графика функции 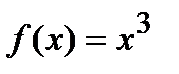 .
.
Найдем вторую производную от заданной функции 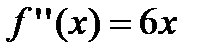 . В силу того, что
. В силу того, что 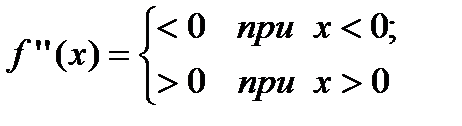 , то график функции
, то график функции 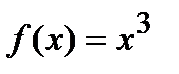 будет выпуклым при отрицательных значениях аргумента и вогнутым при положительных значениях аргумента.
будет выпуклым при отрицательных значениях аргумента и вогнутым при положительных значениях аргумента.
Опр. Точка, отделяющая вогнутую часть графика функции от выпуклой (или выпуклую часть графика функции от вогнутой), называется точкой перегиба.
Выясним необходимые и достаточные условия существования точек перегиба.
Необходимое и достаточное условия существования точки перегиба.
Рассмотрим необходимое условие существования точки перегиба.
Т. Если функция  дважды непрерывно дифференцируема на некотором интервале, содержащем точку перегиба
дважды непрерывно дифференцируема на некотором интервале, содержащем точку перегиба 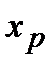 , то в точке перегиба вторая производная равна нулю, т.е.
, то в точке перегиба вторая производная равна нулю, т.е. 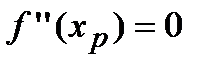 .
.
Обращение в нуль второй производной функции в точке перегиба является необходимым, но не достаточным условием существования такой точки на графике функции.
Пример Доказать, что точка 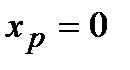 не является точкой перегиба графика функции
не является точкой перегиба графика функции 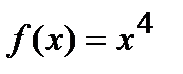 .
.
Если вычислить вторую производную от заданной функции, то она будет равна 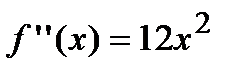 . Если приравнять это выражение к нулю, то получим, что точка
. Если приравнять это выражение к нулю, то получим, что точка 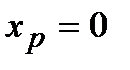 должна быть точкой перегиба графика функции
должна быть точкой перегиба графика функции 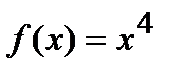 . Однако график этой функции на всей числовой оси является вогнутым, т.е. точка
. Однако график этой функции на всей числовой оси является вогнутым, т.е. точка 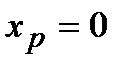 не является точкой перегиба графика функции
не является точкой перегиба графика функции 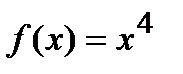 . В связи с этим рассмотрим достаточное условие существования точки перегиба.
. В связи с этим рассмотрим достаточное условие существования точки перегиба.
Т. Пусть функция  дважды непрерывно дифференцируема на некотором интервале, вторая производная которой в точке
дважды непрерывно дифференцируема на некотором интервале, вторая производная которой в точке 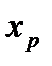 , принадлежащей этому интервалу, обращается в нуль (
, принадлежащей этому интервалу, обращается в нуль ( 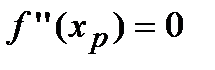 ) или не существует. Если при переходе через точку
) или не существует. Если при переходе через точку 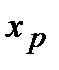 вторая производная функции меняет свой знак, то точка
вторая производная функции меняет свой знак, то точка 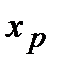 определяет точку перегиба графика функции
определяет точку перегиба графика функции  .
.
Пример Найти точки перегиба и интервалы выпуклости и вогнутости графика функции 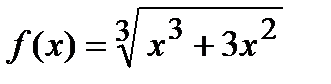 .
.
Найдем вторую производную заданной функции 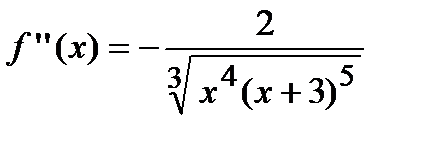 . Найдем точки подозрительные на перегиб: а)
. Найдем точки подозрительные на перегиб: а) 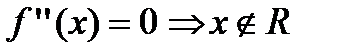 б)
б) 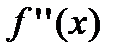 – не существует
– не существует 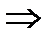 знаменатель дроби обращается в ноль при
знаменатель дроби обращается в ноль при 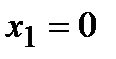 и
и 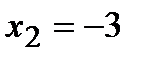 . Отложим эти точки на числовой оси и определим знак второй производной на каждом интервале:
. Отложим эти точки на числовой оси и определим знак второй производной на каждом интервале:
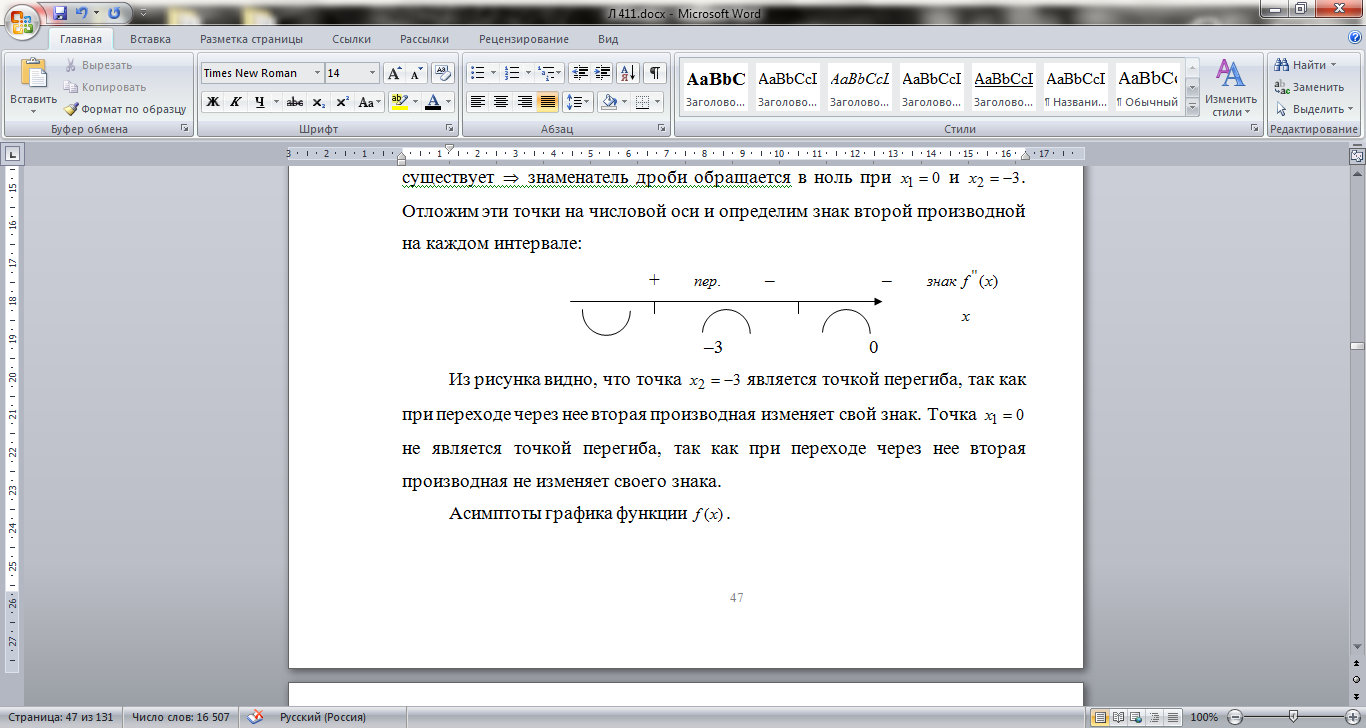
Из рисунка видно, что точка 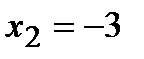 является точкой перегиба, так как при переходе через нее вторая производная изменяет свой знак. Точка
является точкой перегиба, так как при переходе через нее вторая производная изменяет свой знак. Точка 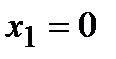 не является точкой перегиба, так как при переходе через нее вторая производная не изменяет своего знака.
не является точкой перегиба, так как при переходе через нее вторая производная не изменяет своего знака.
Асимптоты графика функции  .
.
В большинстве практических случаев необходимо знать поведение функции при неограниченном росте (убыли) аргумента. Одним из наиболее интересных случаев, которые возникают при таком исследовании, является случай, когда график функции неограниченно приближается к некоторой прямой.
Опр. Прямая ( 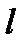 ):
): 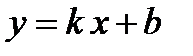 называется асимптотой графика функции
называется асимптотой графика функции 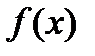 , если расстояние от переменной точки графика до этой прямой стремится к нулю при стремлении аргумента
, если расстояние от переменной точки графика до этой прямой стремится к нулю при стремлении аргумента 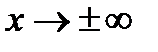 , т.е.
, т.е. 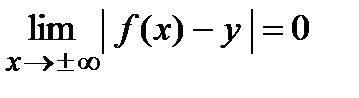 .
.
График функции может приближаться к асимптоте сверху, снизу, слева, справа или колеблясь возле этой прямой. 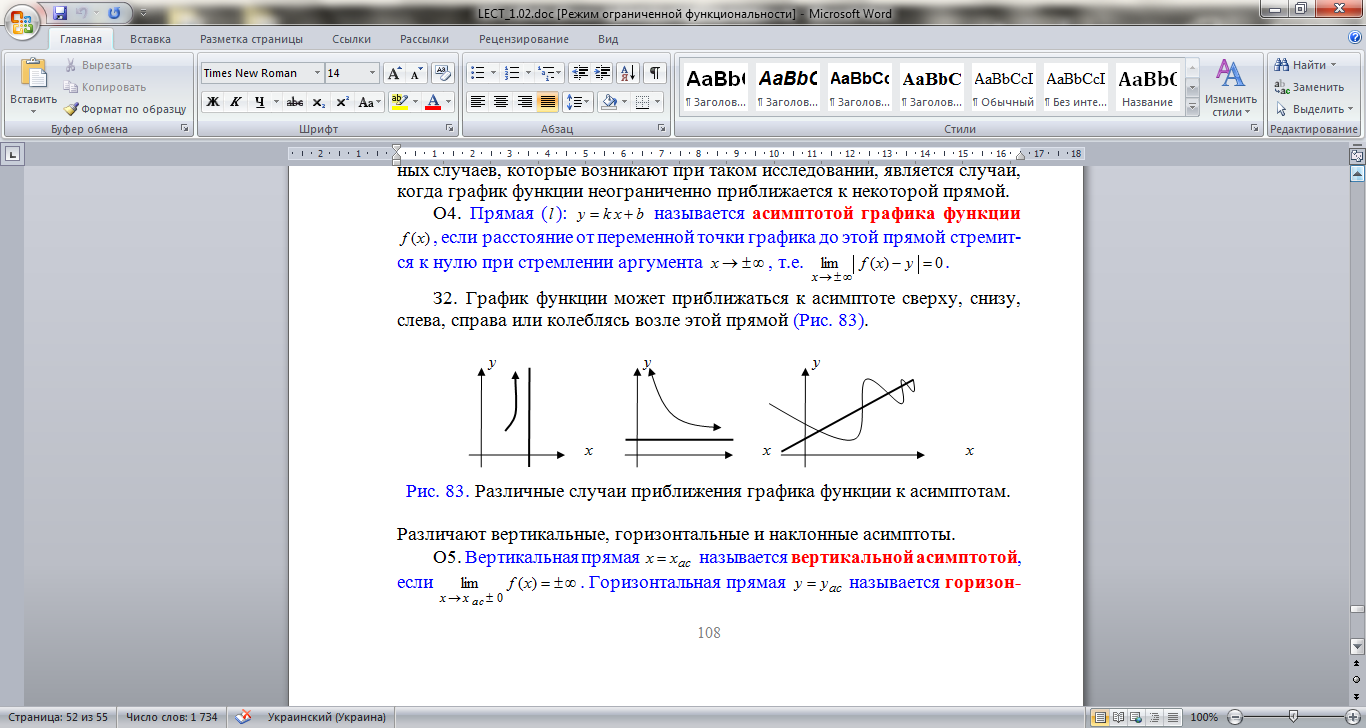
Различают вертикальные, горизонтальные и наклонные асимптоты.
Опр. Вертикальная прямая 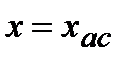 называется вертикальной асимптотой, если
называется вертикальной асимптотой, если 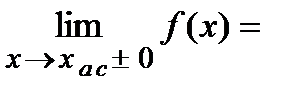
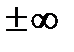 . Горизонтальная прямая
. Горизонтальная прямая 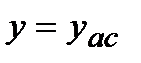 называется горизонтальной асимптотой, если
называется горизонтальной асимптотой, если 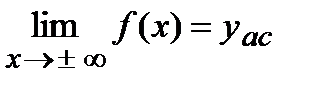 . Прямая
. Прямая 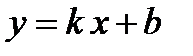 называется наклонной асимптотой (параметр
называется наклонной асимптотой (параметр 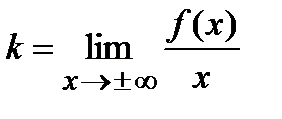 и параметр
и параметр 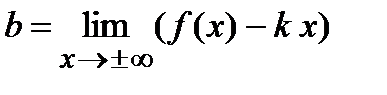 отличаются от
отличаются от 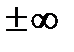 и
и 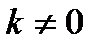 ).
).
Горизонтальная асимптота является частным случаем наклонной асимптоты: если 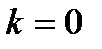 , то наклонная асимптота вырождается в горизонтальную
, то наклонная асимптота вырождается в горизонтальную 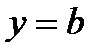 , при условии, что
, при условии, что 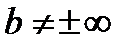 . Если параметр
. Если параметр 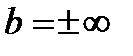 , то горизонтальной асимптоты нет.
, то горизонтальной асимптоты нет.
Полная схема исследования функции с помощью производных.
Из изложенного ранее материала следует следующая схема исследования функции с помощью производных:
1. Находят область определения функции. При наличии точек разрыва II рода изучают поведение функции в их малой окрестности, т.е. вычисляют лево- и правосторонние пределы. При задании функции словесным образом также вычисляют лево- и правосторонние пределы для граничных точек интервалов, на которых функция описывается разными формулами.
2. Находят точки пересечения с координатными осями.
3. Определяют четная, нечетная или общего вида заданная функция.
4. Определяют периодическая или непериодическая заданная функция.
5. Находят критические точки, решая уравнение 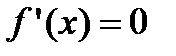 , и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (
, и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания ( 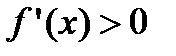 ) и убывания (
) и убывания ( 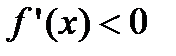 ) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.
) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.
6. Находят точки подозрительные на перегиб, решая уравнение 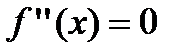 , и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (
, и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости ( 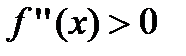 ) и выпуклости (
) и выпуклости ( 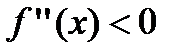 ) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.
) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.
7. Находят асимптоты графика функции.
8. Результаты исследования заносят в сводную таблицу.
9. По данным таблицы строят схематичный график функции.
З4. При нахождении области определения функции надо помнить о действиях, запрещенных в области действительного переменного:
– нельзя делить на нуль, поэтому выражение, стоящее в знаменателе дроби, не должно равняться нулю;
– нельзя извлекать корень четной степени из отрицательного числа, поэтому выражение, стоящее под корнем четной степени, должно быть неотрицательным ( 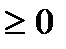 );
);
– основание логарифмической функции должно быть строго положительным и не равным единице;
– выражение, стоящее под логарифмом, должно быть строго положительным;
– выражение, стоящее под знаком 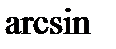 или
или 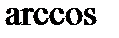 , по модулю не должно превышать единицу (
, по модулю не должно превышать единицу ( 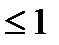 ).
).
Пример Исследовать и построить схематичный график функции 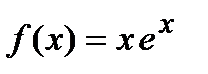 .
.
Используя схему исследования графика функции с помощью производных, найдем:
1. 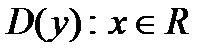 .
.
2. Найдем точки пересечения графика функции с координатными осями
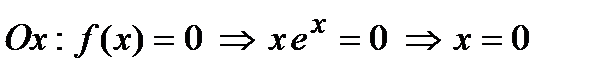 , т.е.
, т.е. 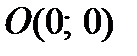 – точка пересечения с осью абсцисс;
– точка пересечения с осью абсцисс;
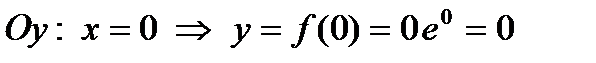 , т.е.
, т.е. 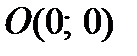 – точка пересечения с осью ординат.
– точка пересечения с осью ординат.
3. Вычислим 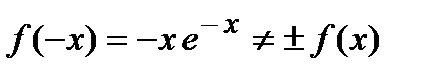 – функция общего вида.
– функция общего вида.
4. Функция непериодическая.
5. Найдем первую производную функции 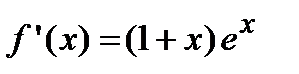 , которая существует на всей числовой оси, следовательно, найдем критические точки, решая уравнение
, которая существует на всей числовой оси, следовательно, найдем критические точки, решая уравнение 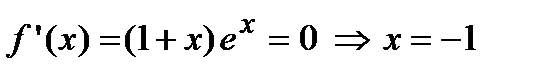 . Отложим найденную точку на числовой оси и определим знак первой производной на каждом интервале
. Отложим найденную точку на числовой оси и определим знак первой производной на каждом интервале 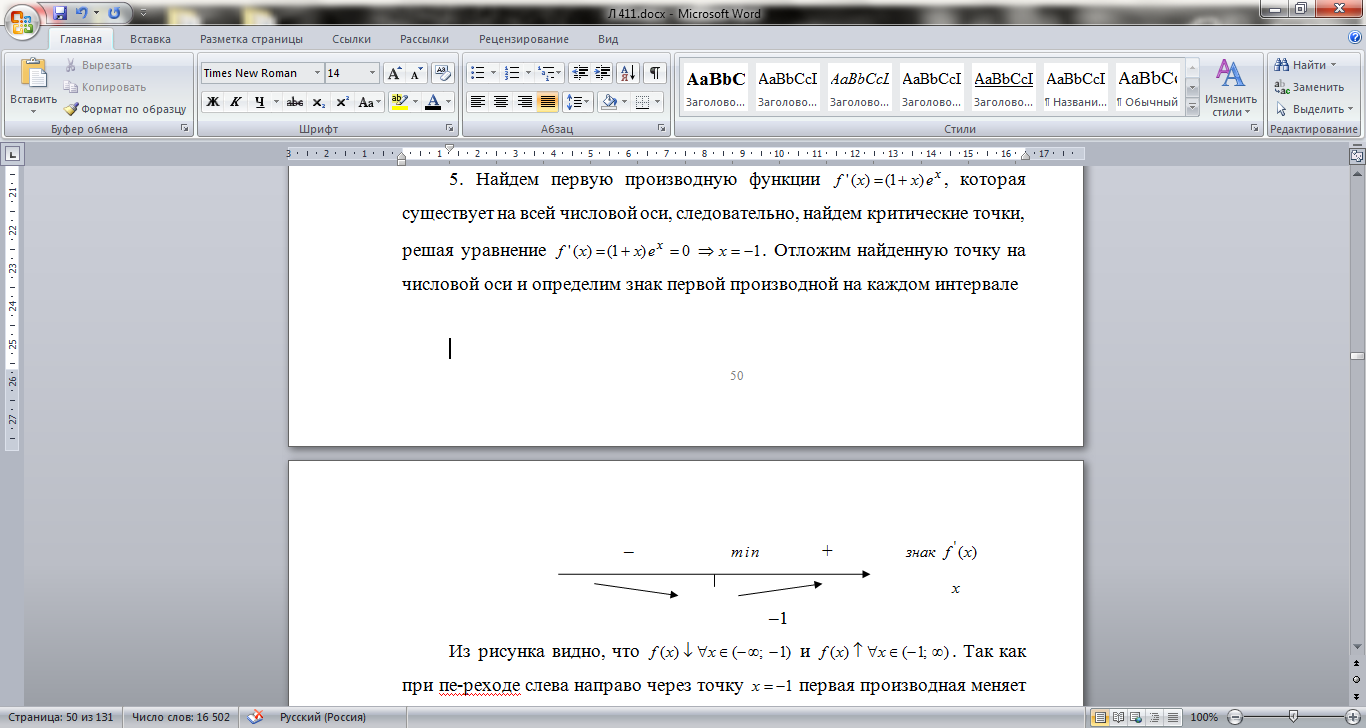
Из рисунка видно, что 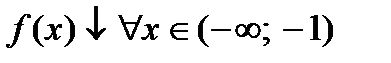 и
и 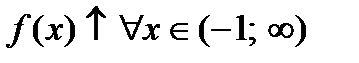 . Так как при переходе слева направо через точку
. Так как при переходе слева направо через точку 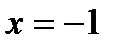 первая производная меняет свой знак с “–” на “+”, то в этой точке наблюдается минимум. Вычислим значение функции в минимуме
первая производная меняет свой знак с “–” на “+”, то в этой точке наблюдается минимум. Вычислим значение функции в минимуме 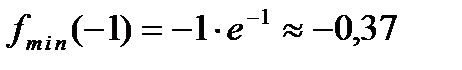 .
.
6. Найдем вторую производную функции 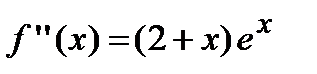 , которая существует на всей числовой оси, следовательно, найдем точки, подозрительные на перегиб, решая уравнение
, которая существует на всей числовой оси, следовательно, найдем точки, подозрительные на перегиб, решая уравнение 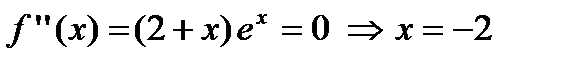 . Отложим найденную точку на числовой оси и определим знак второй производной на каждом интервале
. Отложим найденную точку на числовой оси и определим знак второй производной на каждом интервале
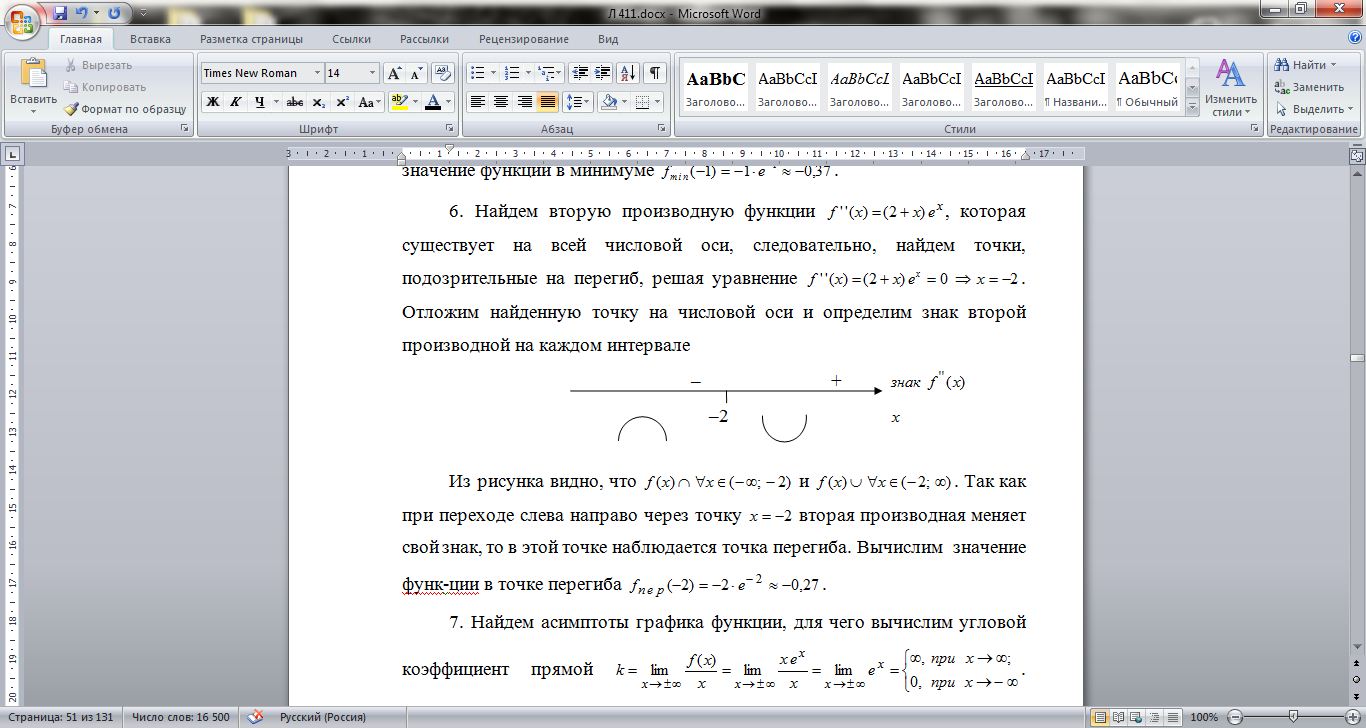
Из рисунка видно, что 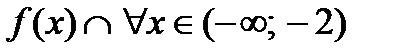 и
и 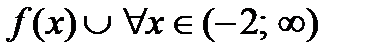 . Так как при переходе слева направо через точку
. Так как при переходе слева направо через точку 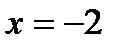 вторая производная меняет свой знак, то в этой точке наблюдается точка перегиба. Вычислим значение функции в точке перегиба
вторая производная меняет свой знак, то в этой точке наблюдается точка перегиба. Вычислим значение функции в точке перегиба 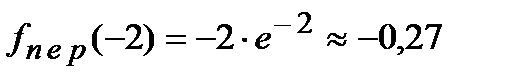 .
.
7. Найдем асимптоты графика функции, для чего вычислим угловой коэффициент прямой 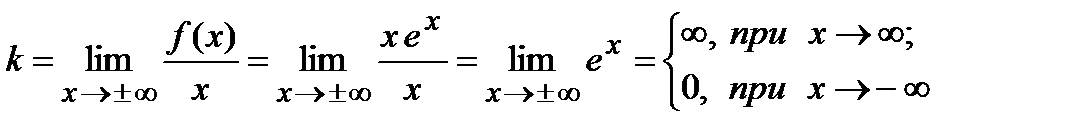 . Таким образом, при
. Таким образом, при 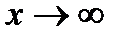 асимптот нет, а при
асимптот нет, а при 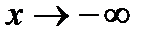 возможна горизонтальная асимптота. Вычислим параметр
возможна горизонтальная асимптота. Вычислим параметр 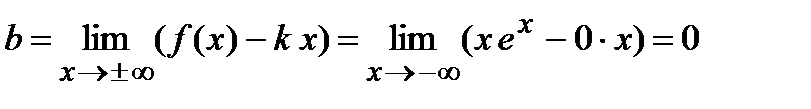 . Следовательно, график заданной функции имеет горизонтальную асимптоту
. Следовательно, график заданной функции имеет горизонтальную асимптоту 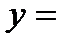
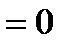 .
.
8. Построим сводную таблицу
| Интервал | 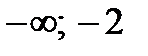
| 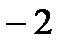
| 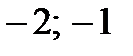
| 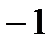
| 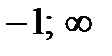
|
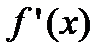
| 
| 
| 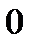
| 
| |
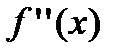
| 
| 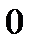
| 
| 
| |
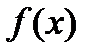
| 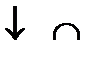
| 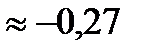
| 
| 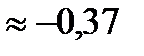
| 
|
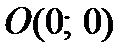 – точка пересечения с координатными осями.
– точка пересечения с координатными осями.
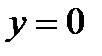 – горизонтальная асимптота.
– горизонтальная асимптота.
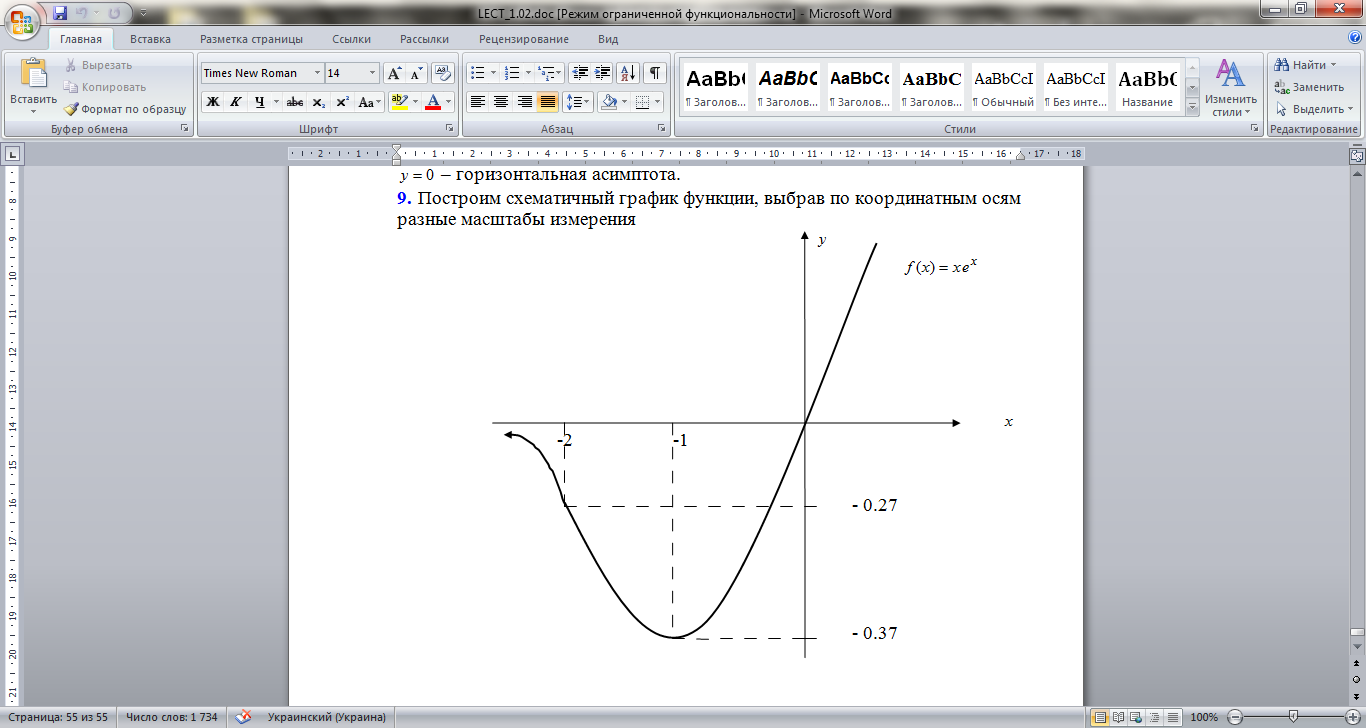
9. Построим схематичный график функции, выбрав по координатным осям разные масштабы измерения
Лекция 9. Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица интегралов. Методы интегрирования: непосредственное интегрирование, метод разложения, метод замены переменной.
При решении многих практических задач таких, как вычисление длин линий, площадей, отыскание траекторий движения и других, вводится понятие интегрирования.
Опр. Первообразной функции 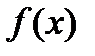 называется такая функция
называется такая функция 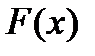 , первая производная от которой равна заданной функции, т.е.
, первая производная от которой равна заданной функции, т.е. 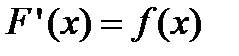 .
.
Т. (о существовании первообразной) Если функция 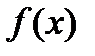 непрерывна на сегменте
непрерывна на сегменте 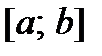 , то на этом интервале существует первообразная этой функции.
, то на этом интервале существует первообразная этой функции.
Т. Если 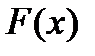 – первообразная функции
– первообразная функции 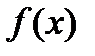 , то функция
, то функция 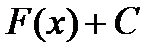 (
( 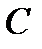 – произвольная постоянная) также является первообразной функции
– произвольная постоянная) также является первообразной функции 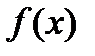 .
.
Док-во. 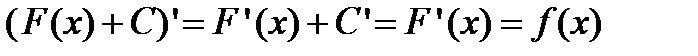 .
.
Т. Если 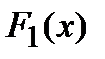 и
и 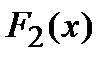 первообразные функции
первообразные функции 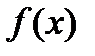 , то они отличаются друг от друга на постоянную величину.
, то они отличаются друг от друга на постоянную величину.
Док-во. Пусть 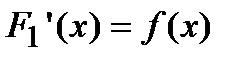 и
и 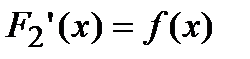 . Введем в рассмотрение вспомогательную функцию
. Введем в рассмотрение вспомогательную функцию 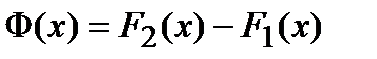 и рассмотрим эту функцию на открытом интервале
и рассмотрим эту функцию на открытом интервале 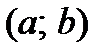 . По теореме Лагранжа для любого интервала
. По теореме Лагранжа для любого интервала 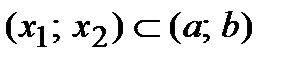 выполняется равенство
выполняется равенство 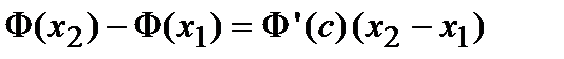 , где
, где 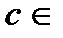
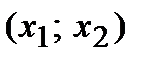 . По условию теоремы
. По условию теоремы 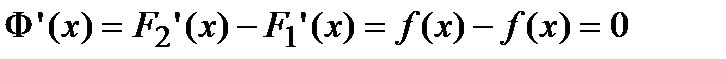 , следовательно,
, следовательно, 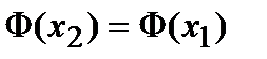 В силу произвольности точек
В силу произвольности точек 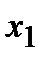 и
и 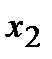 полученное равенство выполняется для всего исследуемого интервала. Это означает, что
полученное равенство выполняется для всего исследуемого интервала. Это означает, что 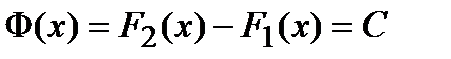 , откуда и вытекает утверждение теоремы.
, откуда и вытекает утверждение теоремы.
Пример Пусть дана функция 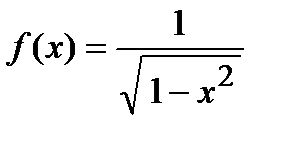 . Найти первообразную этой функции. В случае наличия двух первообразных показать, что они отличаются на постоянную величину.
. Найти первообразную этой функции. В случае наличия двух первообразных показать, что они отличаются на постоянную величину.
Для функции существуют две первообразные 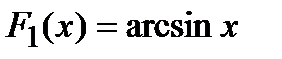 и
и 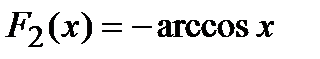 . Их разность
. Их разность 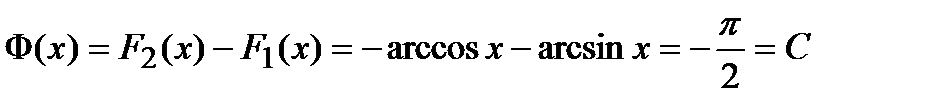 .
.
Опр. Совокупность всех первообразных функции 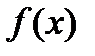 называется неопределенным интегралом и обозначается
называется неопределенным интегралом и обозначается 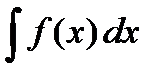 , где
, где 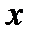 – переменная интегрирования,
– переменная интегрирования, 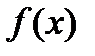 – подынтегральная функция,
– подынтегральная функция, 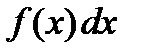 – подынтегральное выражение.
– подынтегральное выражение.
На основании теорем можно записать, что 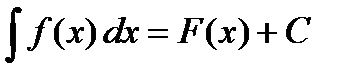 .
.
Опр. Отыскание всех первообразных называется неопределенным интегрированием.
Выясним геометрический смысл неопределенного интеграла. Пусть дана функция 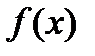 и требуется найти такую кривую
и требуется найти такую кривую 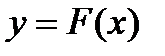 , для которой в каждой ее точке тангенс угла наклона касательной равен значению функции
, для которой в каждой ее точке тангенс угла наклона касательной равен значению функции 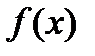 в этой точке. Такой линией будет кривая, для которой
в этой точке. Такой линией будет кривая, для которой 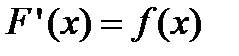 . Таким образом, неопределенный интеграл определяет все кривые, у которых тангенс угла наклона в каждой ее точке совпадает со значением функции
. Таким образом, неопределенный интеграл определяет все кривые, у которых тангенс угла наклона в каждой ее точке совпадает со значением функции 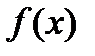 .
.
Пример Построить кривые, которые задаются неопределенным интегралом 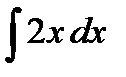 .
.
Первообразной для подынтегральной функции 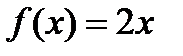 будет функция
будет функция 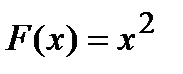 , следовательно,
, следовательно, 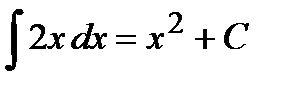 . Построим эти кривые:
. Построим эти кривые:
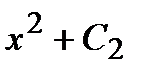
Свойства неопределенного интеграла.
1. Производная от неопределенного интеграла равна подынтегральной функции 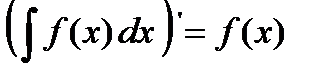 .
.
Док-во. По определению неопределенного интеграла











