Лекция 12. Элементы комбинаторного анализа: размещения, перестановки, сочетания. Формула Ньютона. Случайные события. Вероятность события. Простейшие свойства вероятности.
Теория вероятностей имеет дело с испытаниями, исходы которых непредсказуемы: они зависят от случая. О таких испытаниях мы уже говорили – это подбрасывание монеты и кубика, проверка лотерейных билетов, падение бутерброда на пол и т.д.
Для всех таких испытаний характерно то, что их можно многократно повторять (хотя бы мысленно) в одних и тех же условиях. То есть условия проведения испытания не меняются, а результаты могут быть совершенно различными (такие испытания называют массовыми однородными испытаниями).
Чтобы выяснить, насколько вероятно то или иное случайное событие, связанное с испытанием, нужно подсчитать, как часто оно происходит. Для этого используют два важных теоретико-вероятностных понятия.
Опр.1. Пусть проводится n однородных испытаний, и пусть событие А произошло в m из них, тогда число называется абсолютной частотой появления события А.
Опр.2. Пусть проводится n однородных испытаний, и пусть событие А произошло в m из них. Число равное отношению числа всех проведенных испытаний к числу испытаний, в которых событие А произошло, называется относительной частотой появления события А.
Относительная частота появления события А обозначается: W(А). Таким образом, по определению, 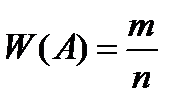 .
.
Зам. Относительную частоту можно найти, поделив абсолютную частоту на число испытаний. Иногда относительную частоту измеряют в процентах.
Пример: игральный кубик подбросили 50 раз, и исходы испытаний занесли в таблицу, в первом строке которой перечислены все возможные исходы, во второй и третьей строках фиксировались значения абсолютной и относительных частот соответственно.
| исходы | ||||||
| абсолютная частота | ||||||
| относительная частота | 0,18 | 0,12 | 0,16 | 0,22 | 0,18 | 0,14 |
Полученная таблица обладает некоторыми замечательными свойствами, которые характерны для любой таблицы абсолютных и относительных частот:
1) сумма абсолютных частот по всем исходам испытания равна числу проведенных испытаний, для данной таблицы – 50;
2) сумма относительных частот по всем исходам испытания равна 1.
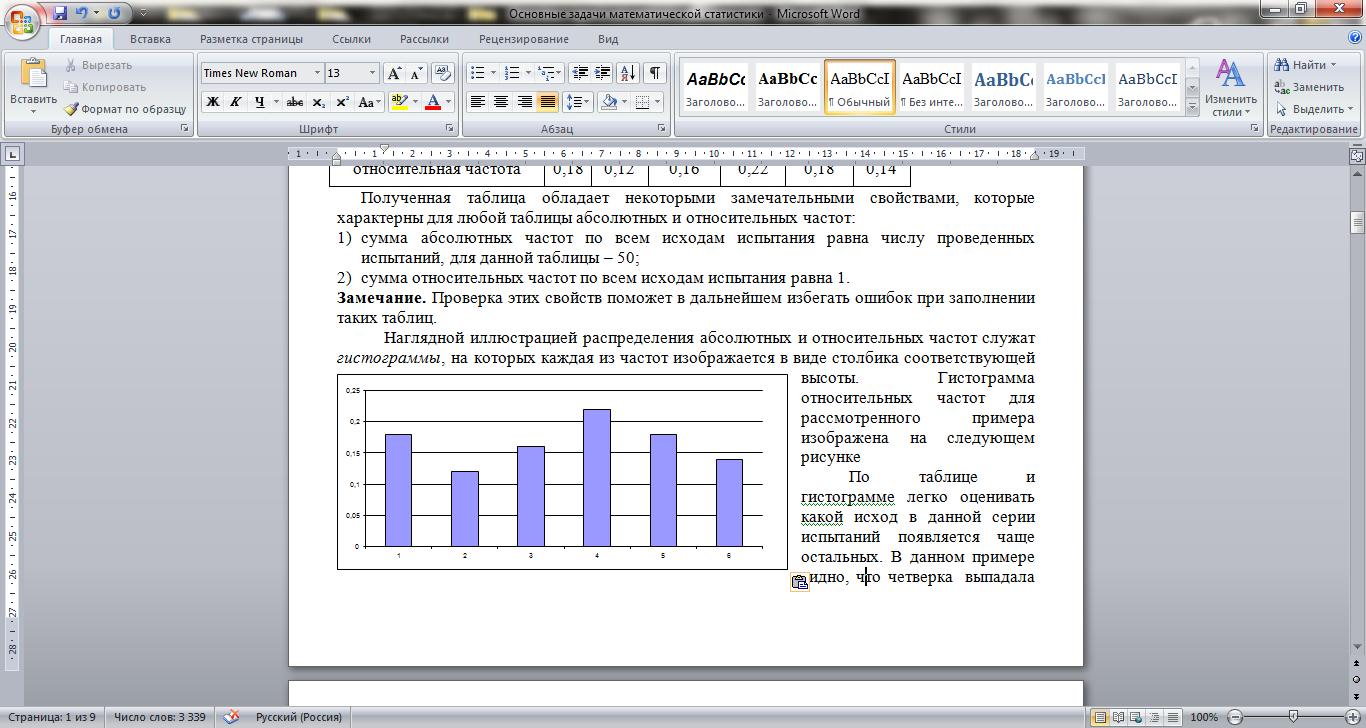 Наглядной иллюстрацией распределения абсолютных и относительных частот служат гистограммы, на которых каждая из частот изображается в виде столбика соответствующей высоты. Гистограмма относительных частот для рассмотренного примера изображена на следующем рисунке
Наглядной иллюстрацией распределения абсолютных и относительных частот служат гистограммы, на которых каждая из частот изображается в виде столбика соответствующей высоты. Гистограмма относительных частот для рассмотренного примера изображена на следующем рисунке
Пусть проводится серия испытаний, и фиксируются абсолютные и относительные частоты исходов испытаний. Выясним, как ведут себя частоты при увеличении числа испытаний в серии. Это удобно наблюдать на конкретном примере.
Пример. Игральный кубик подбрасывали 1000 раз, и после каждой серии их 100 подбрасываний фиксировали относительную частоту появления каждого исхода. В результате была получена следующая таблица.
| Количество испытаний | Частота исходов | |||||
| 0,16 | 0,16 | 0,2 | 0,15 | 0,19 | 0,14 | |
| 0,16 | 0,135 | 0,185 | 0,16 | 0,18 | 0,18 | |
| 0,167 | 0,16 | 0,163 | 0,153 | 0,183 | 0,173 | |
| 0,168 | 0,153 | 0,175 | 0,163 | 0,185 | 0,158 | |
| 0,164 | 0,146 | 0,182 | 0,16 | 0,186 | 0,162 | |
| 0,152 | 0,157 | 0,183 | 0,153 | 0,188 | 0,167 | |
| 0,153 | 0,164 | 0,180 | 0,151 | 0,186 | 0,166 | |
| 0,159 | 0,164 | 0,181 | 0,155 | 0,180 | 0,161 | |
| 0,156 | 0,164 | 0,183 | 0,166 | 0,171 | 0,160 | |
| 0,158 | 0,170 | 0,182 | 0,165 | 0,168 | 0,157 |
Построим график зависимости, например частоты выпадения тройки, от числа экспериментов.
По графику видно, что относительная частота появления тройки вначале проведения серии испытаний испытывает значительные колебания, но с ростом числа испытаний она стабилизируется около значения 0,18. Построив графики зависимостей относительных частот появления других исходов, от числа проведенных испытаний можно убедиться в аналогичном результате. Поэтому, можно сделать вывод, что относительная частота появления той или другой цифра, в данном случае, стабилизируется с ростом числа испытаний.
Оказывается, что такое свойство относительных частот имеет место и в общем случае. Говорят, что с ростом числа однородных испытаний относительная частота появления события приобретает свойство устойчивости, мало отличается от некоторого фиксированного числа. На этом факте основывается одно из определений вероятности.
Опр.3. Статистической вероятностью события А называется число вокруг которого колеблется относительная частота появления события А в длинной серии испытаний.
Замечание. Следует заметить, что данное определение не является математически строгим, оно скорее, экспериментальное.
Случайные величины
Рассмотрим несколько примеров.
Пример 1. Производится восемь выстрелов по мишени, представляющей собой десять концентрических кругов. Рассмотрим всевозможные варианты выбитых очков при каждом выстреле. Это могут быть: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Таким образом, с этим испытанием можно связать вышеуказанную последовательность чисел, причем каждый член этой последовательности появляется случайным образом.
Пример 2. Подбрасывается игральный кубик. Число выпавших очков на верхней грани кубика может быть равно 1; 2; 3; 4; 5; 6. И с этим испытанием мы связываем числовую последовательность, каждый член которой появляется случайным образом.
Пример 3. Света ожидает телефонного звонка от Сергея, который пообещал позвонить в течение десяти минут. Время ожидания Светой телефонного звонка может быть выражено любым действительным числом из интервала (0; 10), причем любое число из этого интервала появляется случайным образом.
Рассмотренные примеры и предыдущий опыт решения теоретико-вероятностных задач позволяет нам говорить о том, что в большинстве случаев с испытанием можно связать конечную или бесконечную числовую последовательность, члены которой появляются случайным образом.
Для описания таких ситуаций в теории вероятностей вводится понятие случайной величины.
Под случайной величиной (СВ) понимают величину, которая в результате испытания принимает то или иное значение, причем неизвестно какое именно. Дадим более строгое математическое определение случайной величины.
Опр. Случайной величиной называется функция, заданная на пространстве элементарных событий данного испытания.
Таким образом, областью определения случайной величины как функции является пространство элементарных событии данного испытания, и множеством значений конечное или бесконечное числовое множество.
Рассмотренные примеры говорят нам о том, что можно провести классификацию случайных величин по множеству их значений. В примерах 1 и 2 случайные величины имели конечной множества значений, в примере 3 случайная величина имеет бесконечное несчетное множество значений.
В теории вероятностей выделяются два класса случайных величин дискретные и непрерывные. Мы подробно остановимся на дискретных случайных величинах.
Опр. Случайная величина, имеющая конечное или счетное множество значений называется дискретной.
Для того чтобы задать дискретную СВ необходимо знать не только множество её значений, но и вероятности появления этих значений. Когда задано и то и другое, то говорят о том, что задан закон распределения вероятностей СВ.
Вернемся к примеру 2. Мы с вами уже знаем, что вероятность появления какой-либо грани симметричного игрального кубика равна 1/6. Поэтому можно составить таблицу распределения вероятностей этой СВ, которая определяется её законом распределения. В первой строке такой таблицы пересилены все возможные значения случайной величины, во второй – соответствующие им вероятности.
| xi | ||||||
| pi | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Закон распределения этой СВ называется равномерным.
В теории вероятностей рассматривают и другие законы распределения дискретных случайных величин.
Пример 4. Ученик 6б класса Костя Сидоров застал двухлетнюю сестренку Катю в момент, когда та инспектировала свой тайник, расположенный в проеме между стеной и книжным шкафом. В тайнике у Кати хранились пуговицы, срезанные в разное время с различных предметов одежды: 5 белых пуговиц с теперь уже не новой папиной рубашки, 3 красные пуговки с маминого халатика и 4 пуговицы с купленной три дня назад Костиной джинсовой куртки. Не обращая внимания на Катины протесты, Костя просунул руку в щель, нащупал 2 пуговицы и вытащил их. Число белых пуговиц оказавшихся у Кости в руках является случайной величиной. Найдем закон распределения этой случайной величины.
Множество значений данной СВ: {0; 1; 2}. Найдем вероятности каждого из значений.
Фактически Костя провел следующее испытание: из 12 пуговиц наугад вытащил две. Тогда число точек в ПЭС этого испытания равно n = С122 = 66.
Значению СВ равному 0 соответствует событие А: среди пуговиц нет ни одной белой. Вероятность этого события можно найти по формуле классической вероятности, но для этого нужно предварительно найти число m исходов благоприятствующих для события А. Благоприятствующими исходами будут пары пуговиц не содержащих ни одной белой. Всего «небелых» пуговиц 7, тогда m = С72 = = 21.
Таким образом, вероятность события А, Р(А) = 21/66 = 7/22, поэтому вероятность значения 0 случайной величины, Р(0) = 7/22.
Аналогично, найдем вероятность значений Р(1) = 35/66 и Р(2) = 10/66.
Тогда таблица распределения вероятностей имеет вид
| xi | |||
| pi | 7/22 | 35/66 | 5/33 |
Заметим, что сумма вероятностей всех значений случайной величины равна 1.
Замечание. Закон распределения случайной величины из примера 4 называется гипергеометрическим. Можно записать общую формулу вычисления вероятностей значений случайной величины, имеющей гипергеометрический закон распределения:
Р(m) = 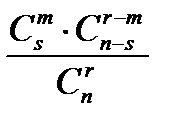
где n – число элементов в множестве, из которого производится выборка;
r – число элементов выборке;
s – число элементов из множества, которые обладают некоторым свойством;
m – значения случайной величины.
При решении некоторых задач достаточно знать достаточно знать не всю таблицу распределения, а некоторое число, которое описывает случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины.
Опр. Математическим ожиданием дискретной случайной величины называется число равное сумме всех произведений значений случайной величины на соответствующие им вероятности: М(Х) = 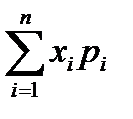 .
.
Зам. Математическое ожидание случайной величины, имеющей равномерный закон распределения, равно среднему арифметическому её возможных значений.
2. Во многих случаях математическое ожидание близко или даже совпадает с наиболее вероятным значением случайной величины.
Пример 5. Математическое ожидание СВ: число выпавших очков при двух подбрасываниях игрального кубика равно 7, и совпадает с наиболее вероятным её значением (проверить самостоятельно).
Опр. Дисперсией дискретной случайной величины называется сумма всех произведений квадратов значений случайной величины на соответствующие им вероятности без квадрата математического ожидания этой случайной величины: 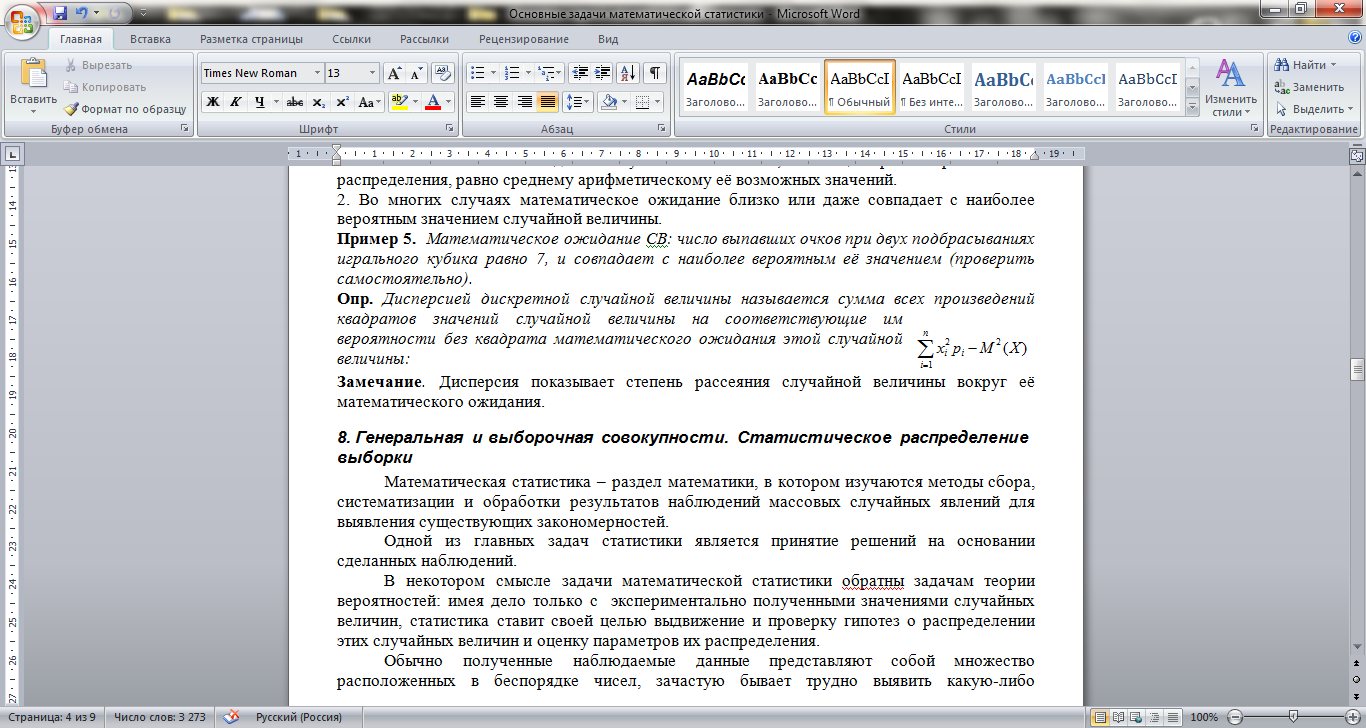
Дата добавления: 2016-06-05; просмотров: 3011;











