Лекция 13. Задачи математической статистики. Выборка. Вариационный ряд.
Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей.
Одной из главных задач статистики является принятие решений на основании сделанных наблюдений.
В некотором смысле задачи математической статистики обратны задачам теории вероятностей: имея дело только с экспериментально полученными значениями случайных величин, статистика ставит своей целью выдвижение и проверку гипотез о распределении этих случайных величин и оценку параметров их распределения.
Обычно полученные наблюдаемые данные представляют собой множество расположенных в беспорядке чисел, зачастую бывает трудно выявить какую-либо закономерность их изменения (варьирования). Для изучения закономерностей (если таковые имеются) варьирования значений, случайной величины опытные данные подвергают обработке.
Пример 1. На телефонной станции проводились наблюдения над числом Х – неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1; 4; 3; 3; 1; 4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3; 2; 7; 2; 0; 0; 1; 3; 3; 1; 2; 4; 2; 0; 2; 3; 1; 2; 5; 1; 1; 0; 1; 1; 2; 2; 1; 1; 5. Здесь, очевидно Х является дискретной случайной величиной, а полученные о ней сведения представляют собой статистические данные.
Операция, заключающаяся в том, что результаты наблюдений над случайной величиной, то есть наблюдаемые значения случайной величины, располагают в порядке неубывания, называется ранжированием опытных данных. После проведения операции ранжирования, данные нетрудно объединить в группы, т.е. сгруппировать так, что в каждой отдельной группе значения случайной величины будут одинаковые. Ранжируем и сгруппируем данные из примера 1.
0; 0; 0; 0; 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 5; 5; 7.
Из полученного ряда чисел видно, что все 60 значений СВ разбиты на семь групп. Таким образом, имеется семь различных значений СВХ: 0; 1; 2; 3; 4; 5; 7.
Опишем рассмотренный пример в терминах математической статистики.
Опр. Совокупность всех подлежащих изучению объектов или результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом, называется генеральной совокупностью.
Опр. Выборочной совокупностью (выборкой) называется совокупность объектов, отобранных случайным образом из генеральной совокупности.
Число объектов в генеральной (выборочной) совокупности называется её объемом и обозначается N (n для выборки).
В примере 1, где наблюдалось число неправильных соединений в минуту на телефонной станции, генеральной совокупностью будет число неправильных соединений в минуту за все время работы станции. Наблюдения, которые представлены в примере 1. являются выборочной совокупностью, объем которой n = 60.
Опр. Ранжированная выборка называется вариационным рядом. Различные элементы вариационного ряда называются вариантами.
Таким образом, в примере 1 СВ Х имеет семь различных вариантов: 0; 1; 2; 3; 4; 5; 7.
Число ni, показывающее сколько раз одна и та же варианта xi встречается в вариационном ряду называется, частотой этой варианты, очевидно, что n = n1 +…+ nk, где k – число различных вариант в заданном вариационном ряду.
В рассмотренном примере варианты имеют следующие частоты: 8; 17; 16; 10; 6; 2; 1 соответственно, и 60 = 8 + 17 + 16 + 10 + 6 + 2 + 1.
Опр. Отношение частоты данной варианты к объему всей выборки называется относительной частотой варианты. Относительная частота варианты хi обычно обозначается wi = 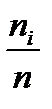 .
.
В нашем примере варианты имеют следующие относительные частоты: 0,13; 0,28; 0,27; 0,17; 0,1; 0,03; 0,02. Заметим, что сумма всех относительных частот равна 1.
Опр. Перечень вариант и соответствующих им частот или относительных частот называется статистическим распределением выборки или статистическим рядом.
| xi | x1 | x2 | … | xk |
| ni | n1 | n2 | … | nk |
| wi | w1 | w2 | … | wk |
СВ Х из примера 1. имеет следующее статистическое распределение частот и относительных частот
| xi | |||||||
| ni | |||||||
| wi | 0,13 | 0,28 | 0,27 | 0,17 | 0,1 | 0,03 | 0,02 |
Для решения многих задач удобно изображать статистическое распределение графически.
Полигоном частот (относительных частот) называют ломаную, отрезки которой соединяют точки с координатами (x1, n1); (x2, n2); …; (xk, nk) (для относительных частот: (x1, w1); (x2, w2); …; (xk, wk)).
Полигон относительных частот СВ Х из примера 1 изображен на рисунке
Дата добавления: 2016-06-05; просмотров: 6535;











