Статистическое оценивание и прогноз
Рассмотрим несколько практических приложений теории вероятностей.
Как говорилось выше, с ростом числа испытаний данной серии частота появления события стремится к его вероятности. Значит, по известной вероятности можнопрогнозироватьчастотуповторения интересующего нас события в будущем. При этом вероятность может быть найдена любым из известных нам способов (в том числе оценена по уже имеющейся частоте).
Пример 1.При проведении контроля качества среди 1000 случайно отобранных деталей оказалось 5 бракованных. Сколько бракованных деталей следует ожидать среди 25 000 деталей?
По результатам контроля можно оценить вероятность события А={произведенная деталь бракованная}. Приближенно она будет равна его частоте:
Р(А) 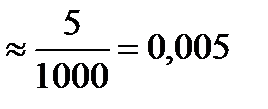
Следует ожидать такую частоту и в будущем, поэтому среди 25 000 деталей окажется около 25 000 • 0,005 = 125 бракованных.
Пример 2. Население города Хабаровска составляет около 400 000 жителей. Сколько хабаровчан родились 29 февраля?
Заметим прежде всего, что вопрос задачи не совсем корректен: мы можем ответить на него лишь приближенно, ибо реальная частота даже в такой большой выборке из 400 000 жителей не обязана совпадать с вероятностью.
29 февраля бывает только в високосном году — один раз в четыре года. Найдем вероятность того, что случайно выбранный хабаровчанин родился 29 февраля следовательно. Воспользуемся классическим определением вероятности:
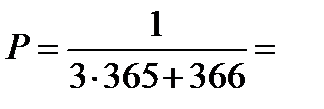
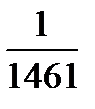 =0,00068
=0,00068
Это значит, что среди 400 000 жителей Хабаровска следует ожидать около 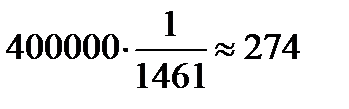 человек, которым приходится праздновать свой день рождения раз в четыре года.
человек, которым приходится праздновать свой день рождения раз в четыре года.
На прогнозировании частоты основан один интересный способ определения численности популяций, используемый в биологии.
Пример 3.Из озера выловили 86 рыб, которых пометили и отпустили обратно в озеро. Через неделю произвели повторный отлов — на этот раз поймали 78 рыб, среди которых оказалось 6 помеченных. Сколько приблизительно рыб живет в озере?
Решить задачу алгебраическими методами не возможно, однако методами теории вероятностей это сделать достаточно несложно.
В самом деле: обозначим неизвестную нам численность рыб в озере через N. Всего помеченных рыб после первого отлова в озере стало 86. Тогда вероятность события А = {выловленная во второй раз рыба оказалась помеченной}, можно вычислить по формуле классической вероятности: 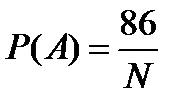 . С другой стороны, относительная частота события А равна: W(A) =
. С другой стороны, относительная частота события А равна: W(A) = 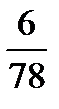 . Так как
. Так как 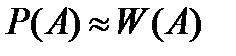 , имеем приближенное равенство:
, имеем приближенное равенство: 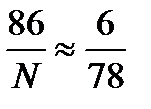 . Отсюда имеем:
. Отсюда имеем: 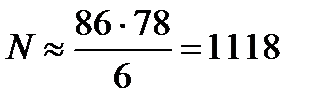 . Таким образом, основываясь на результатах проведенных испытаний, мы получили, что в озере приблизительно живет 1118 рыб.
. Таким образом, основываясь на результатах проведенных испытаний, мы получили, что в озере приблизительно живет 1118 рыб.
Сравнивая вероятности всех возможных исходов испытания, можно предсказать, каким из них эксперимент закончится скорее всего. Обратите внимание, что мы говорим «скорее всего», а не «наверняка» — ведь любой статистический прогноз может оказаться ошибочным.
Пример 4.Какая сумма, скорее всего, выпадет при бросании двух кубиков?
Используя алгоритм вычисления вероятности в КСИ можно найти вероятности появления всех возможных сумм при бросании двух игральных кубиков:
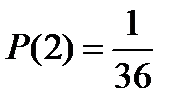 ;
; 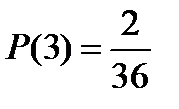 ;
; 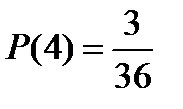 ;
; 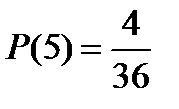 ;
; 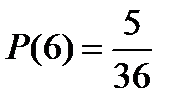 ;
; 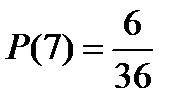 ;
;
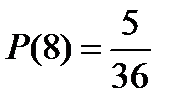 ;
; 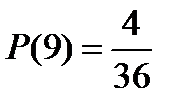 ;
; 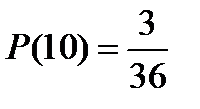 ;
; 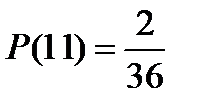 ;
; 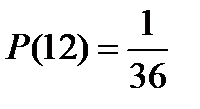 .
.
Так как вероятность выпадения суммы 7 на двух игральных кубиках самая большая, то при бросании двух игральных кубиков семь очков будет выпадать чаще, чем все остальные суммы.
Замечание. Рассмотренные примеры относятся к двум важнейшим типам статистических задач:
- оценка частоты появления события по известной вероятности;
- прогнозирование наиболее вероятного исхода данного испытания.
Рассмотрим теперь пример задачи, в которой по полученным в результате проведенного испытания данным нужно проверить правильность выдвинутой гипотезы.
Пример 5. В 10 бросаниях монеты было получено 9 «орлов». Следует ли считать монету правильной?
В условии задачи поставлена под сомнение гипотеза о правильности подбрасываемой монеты.
Если бы монета была правильной, т.е. выпадение «орла» и «решки» были бы равновозможными, то получить 9 или 10 «орлов» в 10 бросаниях можно было бы с вероятностью 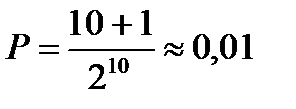 .
.
Значит, в результате опыта произошло очень редкое, маловероятное событие. В то же время, если предположить, что монета неправильная и вероятность выпадения «орла» на ней больше, чем 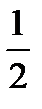 , то произошедшее событие уже не будет таким невероятным. Это дает нам все основания считать, что монета несимметричная.
, то произошедшее событие уже не будет таким невероятным. Это дает нам все основания считать, что монета несимметричная.
Замечание. Рассмотренная выше задача относится к широкому классу статистических задач по проверке статистических гипотез.
Дата добавления: 2016-06-05; просмотров: 6783;











