Операции над множествами

Имеется целый ряд операций, позволяющих получать одни множества из других. Рассмотрим основные из них.

Объединением множеств A и B называется множество

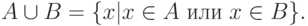
Объединением семейства множеств называется множество

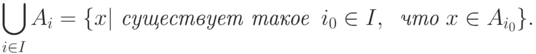
Пересечением множеств A и B называется множество

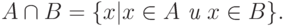
Пересечением семейства множеств 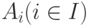называется множество

Из определения операций объединения и пересечения непосредственно следует, что они обладают свойствами ассоциативнос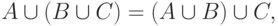ти: и коммутативности

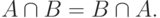
Разностью множеств A и B называется множество

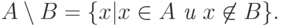
Обычно все рассматриваемые множества являются подмножествами некоторого "универсального" множества U. Разность U \ Aназывается дополнением множества A (в U ) и обозначается через 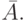Ясно, что и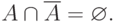

Симметрической разностью множеств A и B называется множество

Иногда симметрическую разность множеств называют дизъюнктивной суммой и обозначают или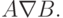

Декартовым (прямым) произведением множеств A₁, ... , A_n называется множество n -ок

Если A₁= ... =A_n=A, то A₁ x ... A_n называется декартовой (прямой) степенью множества A и обозначается через Aⁿ .

Пример. Пусть заданы множества A= {0,1,... ,n} и B={0,1,... m}, где и 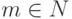- числа и n < m.

Тогда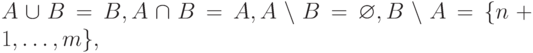

A x B = {(i,j)| 0 <= i <= n, 0 <= j <= m}.