Как доказывать равенство множеств?
Многие математические утверждения, в том числе и многие теоремы в этой книге, имеют следующую форму. Даны разные определения двух множеств A и B. Требуется доказать, что A = B.
Стандартный способ доказательства такого утверждения состоит в доказательстве двух утверждений о включениях:
1. 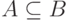 и
и
2. 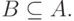
Доказательства этих включений проводятся по такой схеме: рассматривается произвольный элемент, удовлетворяющий определению меньшего множества (слева от знака 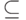 ), и устанавливается, что он удовлетворяет также определению большего множества (справа от знака
), и устанавливается, что он удовлетворяет также определению большего множества (справа от знака 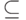 ).
).
В качестве примера докажем одно из свойств (законов) дистрибутивности для операций объединения и пересечения:
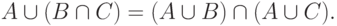
1. Пусть a - произвольный элемент из 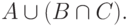 Тогда по определению операции
Тогда по определению операции  имеем
имеем 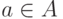 или
или 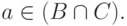 В первом случае из того же определения выводим, что
В первом случае из того же определения выводим, что 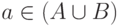 и
и 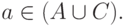 Но тогда по определению операции
Но тогда по определению операции  получаем, что
получаем, что  Во втором случае из определения
Во втором случае из определения  следует, что
следует, что 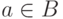 и
и 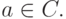 Из этого и из определения
Из этого и из определения  снова следует, что
снова следует, что 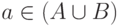 и
и 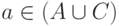 и
и  Таким образом, мы установили, что
Таким образом, мы установили, что 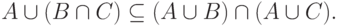
2. Пусть теперь  Тогда по определению операции
Тогда по определению операции  имеем
имеем 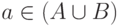 и
и 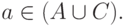 Если
Если 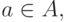 то оба эти включения выполнены. Но тогда
то оба эти включения выполнены. Но тогда 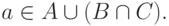 Если же
Если же 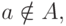 то из первого включения следует, что
то из первого включения следует, что 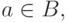 а из второго -
а из второго - 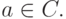 Следовательно,
Следовательно, 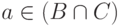 и
и 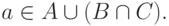 Таким образом,
Таким образом, 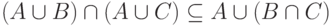 и наше утверждение доказано.
и наше утверждение доказано.
Используя эту же схему, можно установить много других свойств введенных выше операций над множествами и связей между ними.
Дата добавления: 2016-06-05; просмотров: 5375;











