Індивідуальний прогноз

Якщо нас цікавить індивідуальний прогноз величини Y для Y₀, відповідної заданій величині Х₀, то краща лінійна незміщена оцінка Y₀ також подається формулою (3.6.1), але її дисперсія має вигляд

.

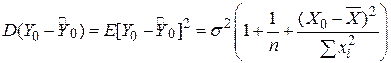(3.9.7)

Можна показати, що Y₀ також підкоряється нормальному закону розподілу з математичним сподіванням і дисперсією, заданими формулами (3.6.1) і (3.6.6) відповідно. Підставляючи 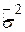замість невідомої 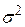можна показати, що

,

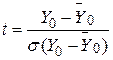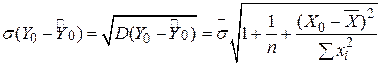
також підкоряється розподілу Ст’юдента. Отже, цей закон розподілу може бути застосований для висновку про істинне значення Y_0. Продовжуючи дослідження моделі “споживання - дохід”, ми знаходимо, що прогнозована точка Y₀=75,3645 така ж, як і 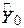, і її дисперсія є

,

.

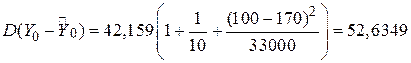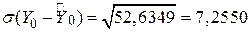Отже, 95%-й довірчий інтервал для Y₀, відповідного Х₀=100, визначається таким чином:

.

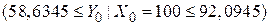(3.9.8)

Порівнюючи цей інтервал з (3.6.5), ми бачимо, що довірчий інтервал для індивідуального Y₀ ширший, ніж за тих же умов довірчий інтервал для середнього значення E(Y|X₀). Обчисливши подібні довірчі інтервали для різних значень Х з табл. 1.3, ми отримаємо 95%-ву довірчу область для індивідуальних значень Y при даних значеннях Х. Ця довірча область зображена на рис.3.6, як і довірча область для .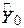

Звернемо увагу на важливу властивість довірчих областей, зображених на рис.3.6. Ширина цих областей найменша при 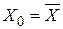(див. вирази для дисперсій і доданок у них 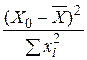). Ширина областей довіри збільшується в міру віддалення Х₀ від 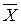. Така поведінка свідчить про те, що здатність прогнозу зменшується в міру віддалення Х₀ від .

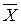Отже, потрібно дуже обережно екстраполювати лінії історичної регресії для прогнозу E(Y|X₀) або Y₀ для заданого Х₀, що знаходиться на значній відстані від 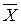– середнього значення за вибіркою.