Анализ подходов прогнозной экстраполяции
В практических исследованиях в качестве модели тренда в основном используют следующие функции:
линейную 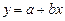 ;
;
квадратичную 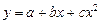 ;
;
параболу третьей степени 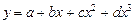 ;
;
степенную 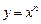 ; показательную
; показательную 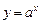 ;
;
экспоненциальную 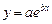 ;
;
модифицированную экспоненциальную 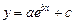 ;
;
логистическую 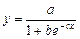 .
.
Особенно широко применяется линейная, или линеаризуемая, то есть сводимая к линейной, форма, как наиболее простая и в достаточной степени удовлетворяющая исходным данным. В этом случае при постановке динамической задачи прогнозирования уравнение регрессии имеет вид
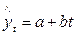 , (6.1)
, (6.1)
где 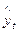 – вычисленное значение
– вычисленное значение 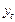 , соответствующее моменту времени t.
, соответствующее моменту времени t.
а и b – константы, которые обращают сумму квадратов отклонений фактических значений 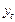 от вычисленных
от вычисленных 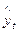 в минимум.
в минимум.
Напомним, что используя метод наименьших квадратов, можно составить систему линейных уравнений, решая которую, сравнительно просто получить значения a и b.
Сущность метода наименьших квадратов (МНК) состоит в отыскании параметров модели тренда, минимизирующих ее отклонение от точек исходного временного ряда, то есть
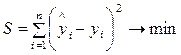 , (6.2)
, (6.2)
где 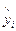 – расчетные значения исходного ряда;
– расчетные значения исходного ряда;
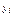 – фактические значения исходного ряда;
– фактические значения исходного ряда;
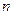 – число наблюдений.
– число наблюдений.
Если модель тренда представить в виде
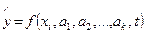 ,
,
где 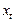 – независимые переменные;
– независимые переменные;
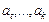 – параметры модели;
– параметры модели;
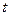 – время,
– время,
то, для того, чтобы найти параметры модели, удовлетворяющие условию (6.1), необходимо приравнять к нулю первые производные величины S по каждому из коэффициентов 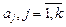 . Решая полученную систему уравнений с k неизвестными, находим значения коэффициентов a.
. Решая полученную систему уравнений с k неизвестными, находим значения коэффициентов a.
Использование процедуры оценки, основанной на МНК, предполагает обязательное соответствие определенному ряду предпосылок, невыполнение которых может привести к значительным ошибкам.
1. Нормальность. Случайные ошибки (значение случайной компоненты) имеют нормальное распределение.
2. Случайные ошибки имеют нулевую среднюю, конечные дисперсии и ковариации.
3. Дисперсии каждой случайной ошибки одинаковы, их величины независимы от значений наблюдаемых переменных.
4. Отсутствие автокорреляции ошибок, то есть значения ошибок, различных наблюдений независимы друг от друга.
5. Значение наблюдаемых переменных свободны от ошибок измерения и имеют конечные средние значение и дисперсии.
После того, как определены коэффициенты модели (6.2), может быть осуществлен точечный и интервальный прогнозы для момента времени tk.
Рассмотренный механизм метода наименьших квадратов позволяет с необходимой точностью аппроксимировать действительное развитие процесса с помощью полиномиального тренда, то есть представить зависимую переменную y как функцию времени в виде многочлена
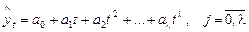 , (6.3)
, (6.3)
где 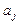 – параметры;
– параметры;
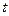 – время;
– время;
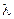 – степень полинома.
– степень полинома.
Оценки параметров  получают, исходя из решения системы нормальных уравнений, развернутая запись которых имеет вид (здесь, как и ранее, переменные xi заменены на характеристики времени ti;
получают, исходя из решения системы нормальных уравнений, развернутая запись которых имеет вид (здесь, как и ранее, переменные xi заменены на характеристики времени ti;
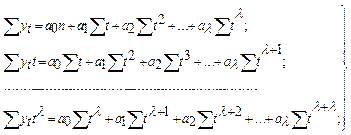 (6.4)
(6.4)
где n – число членов в динамическом ряду.
Система уравнений (6.4), состоящая из l уравнений, содержит в качестве известных величин 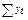 ,
, 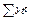 , …,
, …, 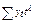 (то есть суммы наблюдаемых значений уровней динамического ряда, умноженные на показатели времени в степени 0, 1, 2, …, l и l неизвестных величин at ).
(то есть суммы наблюдаемых значений уровней динамического ряда, умноженные на показатели времени в степени 0, 1, 2, …, l и l неизвестных величин at ).
Необходимо отметить, что системы для оценивания параметров полиномов невысоких степеней достаточно просты. Обозначим последовательные параметры полиномов как a, b, c, d. Тогда нормальные уравнения для оценивания квадратичной модели примут вид
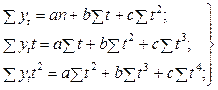 ,
,
для параболы третьей степени получим
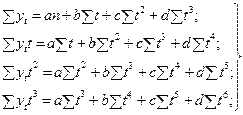 .
.
Как показывает анализ большого количества источников полиномы выше третьей степени при обработке динамических рядов встречаются крайне редко.
Составление нормальных уравнений можно упростить, воспользовавшись тем, что величины 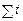 ,
, 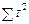 , … не зависят от конкретных значений (уровней) динамического ряда. Если последний состоит из уровней, равноотстоящих друг от друга (а именно с такими рядами чаще всего имеет дело исследователь), то суммы
, … не зависят от конкретных значений (уровней) динамического ряда. Если последний состоит из уровней, равноотстоящих друг от друга (а именно с такими рядами чаще всего имеет дело исследователь), то суммы 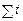 ,
, 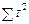 , … являются функциями только числа членов в динамическом ряду. Для них легко получить расчетные формулы, в частности
, … являются функциями только числа членов в динамическом ряду. Для них легко получить расчетные формулы, в частности
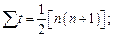
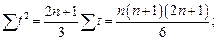
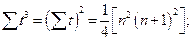
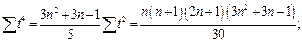
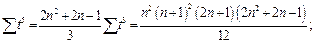
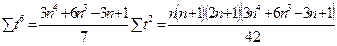 .
.
Во всех приведенных здесь формулах суммирование производится от t=1 до t=n. Значения сумм табулированы для широкого диапазона величин n.
В качестве примера в таблице 6.1 приведены данные динамического ряд выпуска продукции предприятия.
Таблица 6.1 – Cводная таблица для оценки параметров линейной регрессии
| T, год | |||||||
| t | |||||||
| yt, шт. | |||||||
| ytt | |||||||
| T, год | |||||||
| t | |||||||
| yt, шт. | |||||||
| ytt |
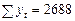 ,
, 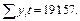
В соответствии с вышеприведенными формулами
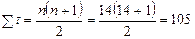 ;
;
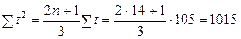 .
.
Решение системы нормальных уравнений применительно к парной линейной регрессии дает:
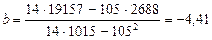 ;
;
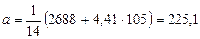 .
.
Уравнение регрессии, следовательно, имеет вид
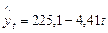 ,
,
а точечный прогноз, например, на 2009 год (tk=17) будет равен
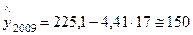 объектов.
объектов.
Таким образом, собственно экстраполяция дает точечную прогностическую оценку. Интуитивно ощущается недостаточность такой оценки и необходимость получения интервальной оценки с тем чтобы прогноз, охватывая некоторый интервал значений прогнозируемой переменной, был бы более надежным или, другими словами, более достоверным и точным.
Дата добавления: 2018-05-10; просмотров: 1500;











