Лекция 7. Определение производной. Геометрический смысл производной. Механический смысл производной. Производные основных элементарных функций.

Приращение аргумента и функции.

Пусть дан график непрерывной функции.

Опр. Разность между конечным и начальным значениями аргумента называется его приращением, т.е. 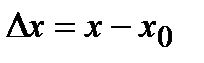. При этом функция получает при-ращение :

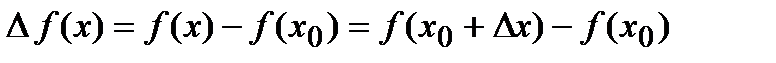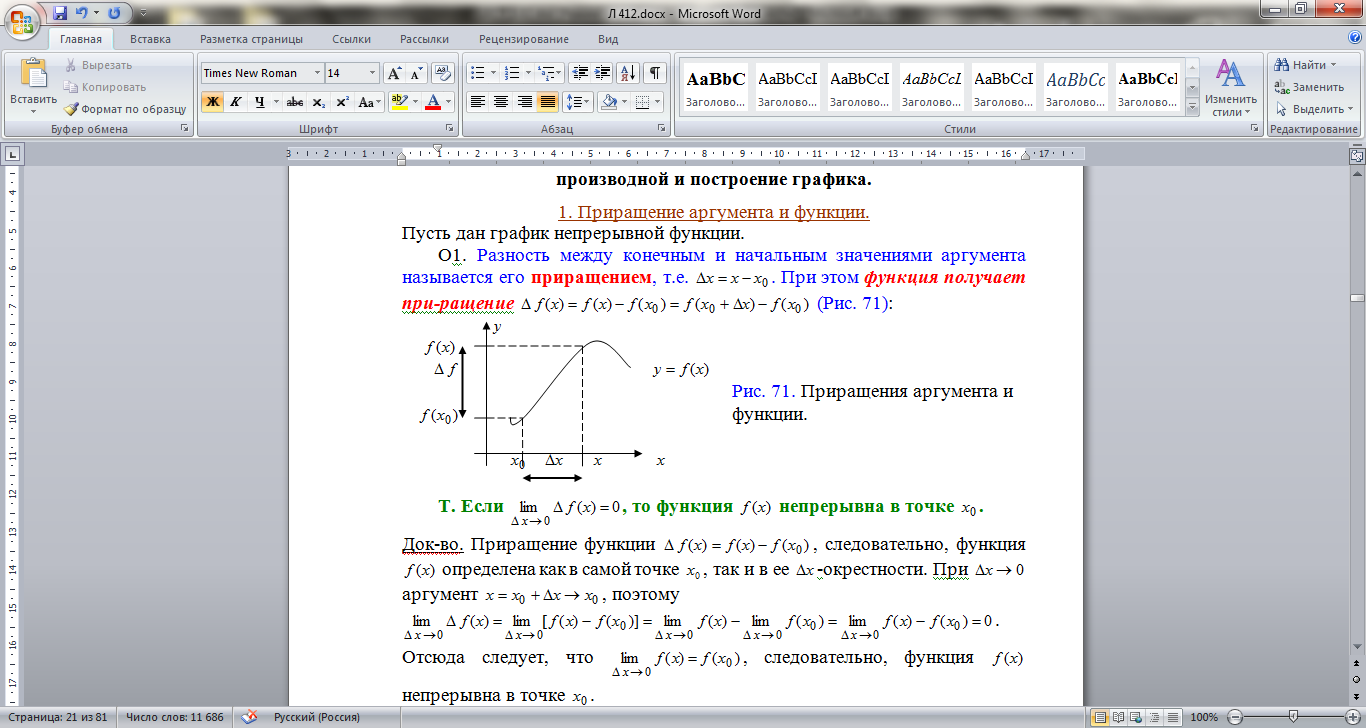
Т. Если 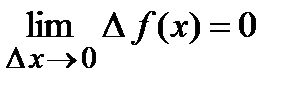, то функция 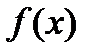непрерывна в точке .

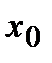Док-во. Приращение функции 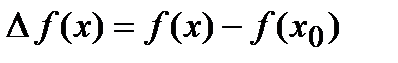, следовательно, функция 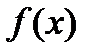определена как в самой точке 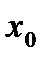, так и в ее 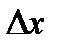-окрестности. При 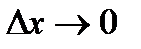аргумент 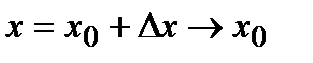, поэтому

.

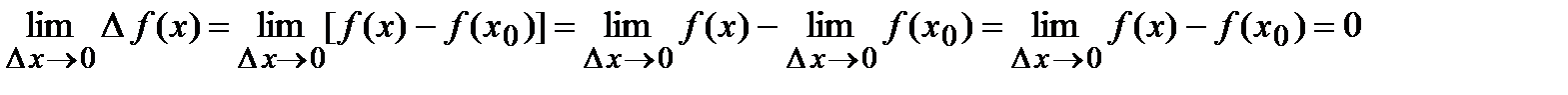Отсюда следует, что 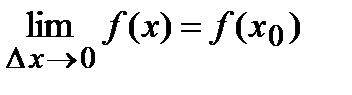, следовательно, функция непрерывна в точке .

Задачи, приводящие к понятию производной.

Пусть материальная точка движется прямолинейно согласно закону 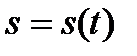, где 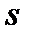– путь, который проходит точка за время 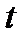. Требуется определить скорость движения точки в момент времени 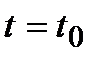. Обозначим через 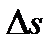путь, пройденный за время 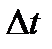. Очевидно, что 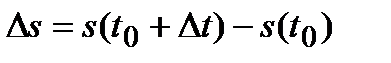. Средняя скорость, с которой движется точка определяется как 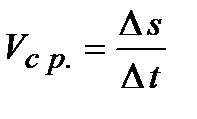. Для того чтобы определить скорость в момент времени 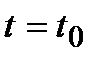, вычислим предел

.

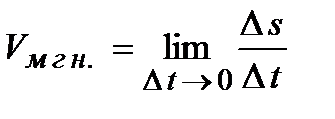Пусть дан график функции 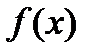. Требуется найти такую прямую линию, которая касается графика функции 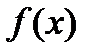только в одной точке .

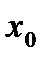Опр. Касательной называется предельное положение секущей прямой 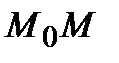при стремлении 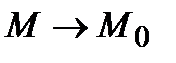произвольным образом.

Вычислим тангенс угла наклона секущей 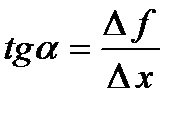. Следовательно, тангенс угла касательной к положительному направлению оси абсцисс будет равен предельному значению приведенной выше величины .

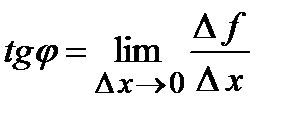Производная функции. Ее механический и геометрический смысл.

Опр. Производной функции 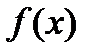в точке 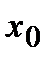называется предел отношения приращения функции 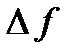к приращению аргумента 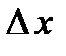при стремлении последней величины к нулю произвольным образом, т. е. .

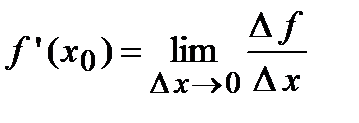Из рассмотренных выше задач следует, что с точки зрения механики производная определяет мгновенную скорость движения, а с геометрической точки зрения производная функции равна тангенсу угла наклона касательной к положительному направлению оси абсцисс в заданной точке, в которой вычисляется значение производной.

Уравнение касательной и нормали 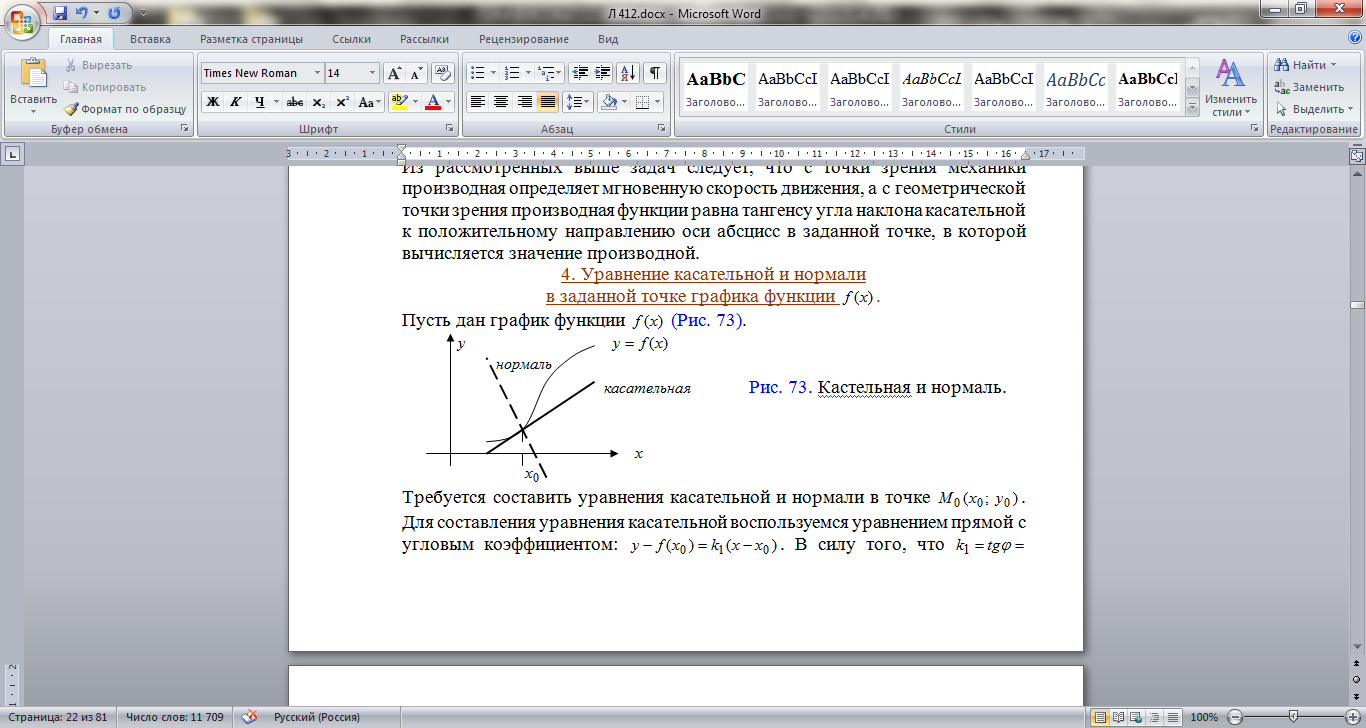в заданной точке графика функции .

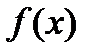Пусть дан график функции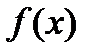

Требуется составить уравнения касательной и нормали в точке 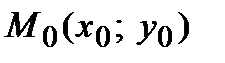. Для составления уравнения касательной воспользуемся уравнением прямой с угловым коэффициентом: 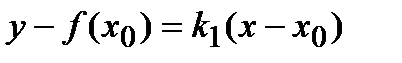. В силу того, что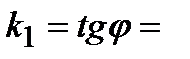 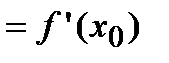, уравнение касательной имеет вид: 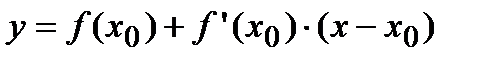. Так как нормаль перпендикулярна к касательной, то ее угловой коэффициент 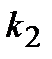связан с угловым коэффициентом касательной соотношением: 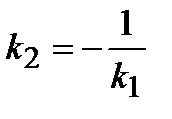. Следовательно, уравнение нормали имеет следующий вид: .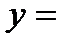

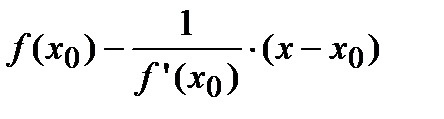Пример Найти угловой коэффициент касательной в точке 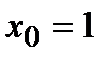к графику функции .

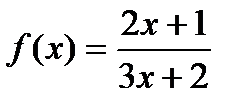Так как 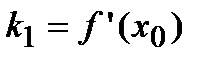, то вычислим производную функции, используя определение производной: ;

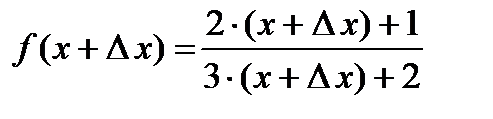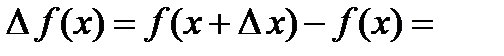
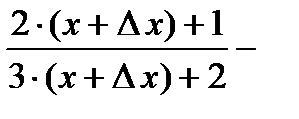
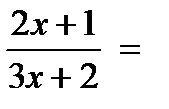
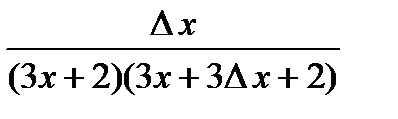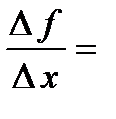
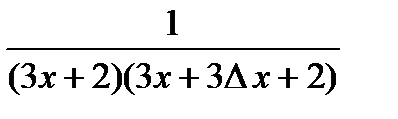; ; следовательно,

.

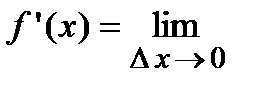
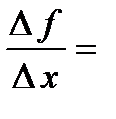
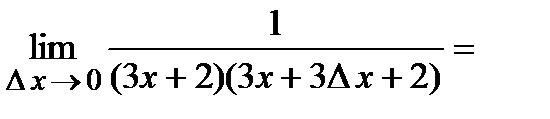
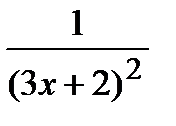Вычислим значение производной в точке 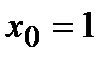, а тем самым и угловой коэффициент касательной в заданной точке .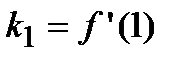

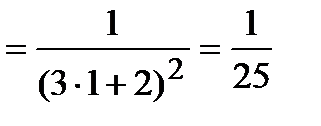Пример Составить уравнение касательной для предыдущего примера (самостоятельно).

Дифференцируемость непрерывных функций.

Опр. Нахождение конечной производной от непрерывной функции называется дифференцированием.

Т. Если функция 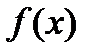дифференцируема в точке 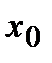, то в этой точке функция 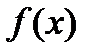непрерывна.

Док-во. Если функция 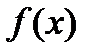дифференцируема в точке 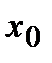, то в этой точке существует конечный предел 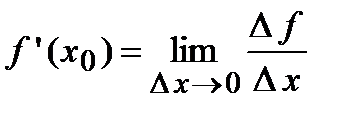. Используя свойство 4 для бесконечно малых функций, можно записать, что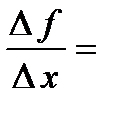 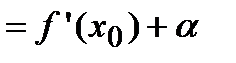, где 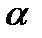– бесконечно малая функция в 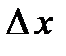-окрестности точки 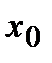. Отсюда следует, что 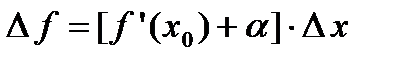. Вычислим предел этого выражения при 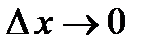. Так как при 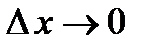функция 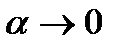, как бесконечно малая функция, а производная остается неизменной, то

.

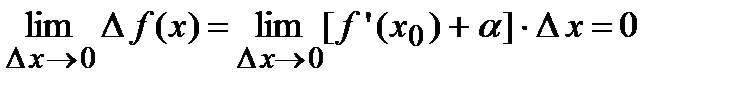По Т получаем, что функция 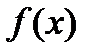непрерывна в точке 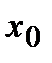. В силу произвольности точки 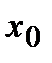функция 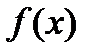будет непрерывна в любой точке своей области определения.

Утверждение, обратное к рассмотренному в Т2, что всякая непрерывная в точке 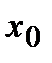функция будет в этой точке дифференцируема, будет верным не во всех случаях, т.е. не всякая непрерывная функция является дифференцируемой.

Пример Дифференцируема ли функция 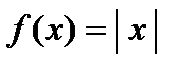в точке .

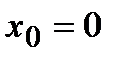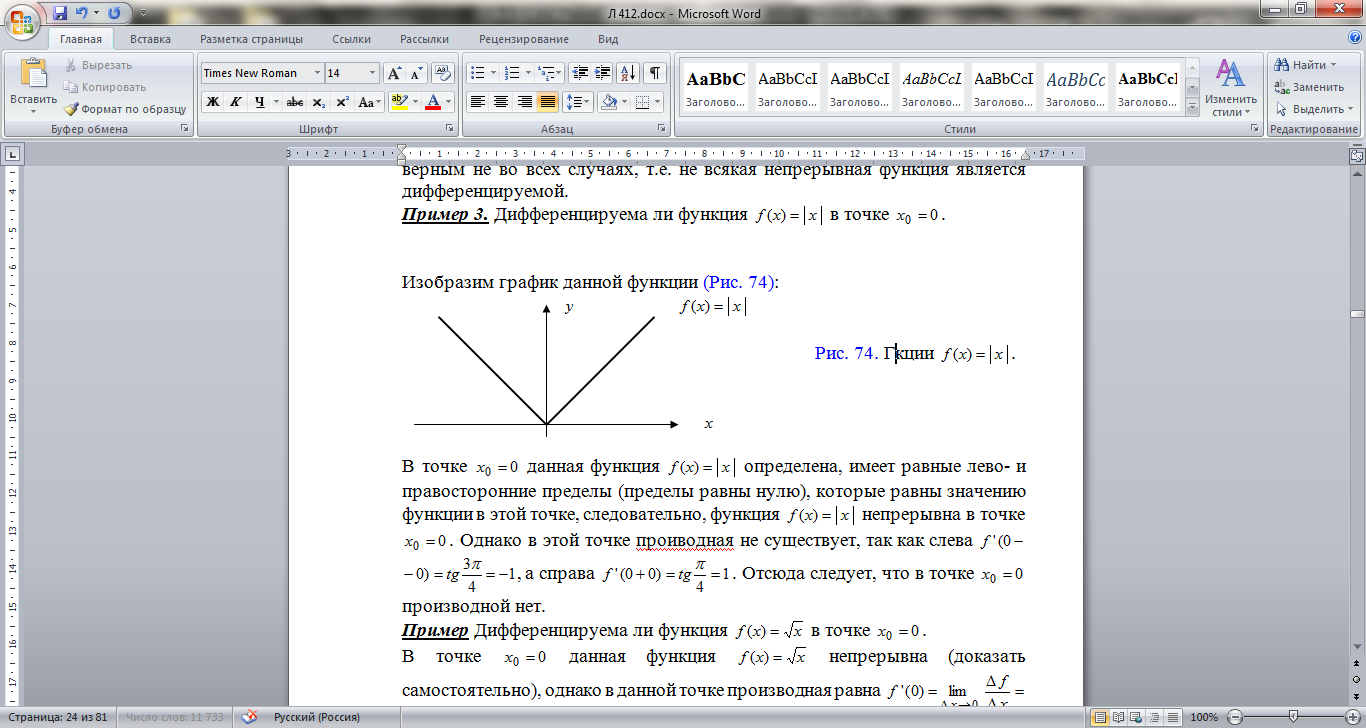Изобразим график данной функции

В точке 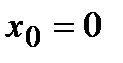данная функция 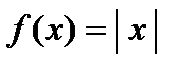определена, имеет равные лево- и правосторонние пределы (пределы равны нулю), которые равны значению функции в этой точке, следовательно, функция 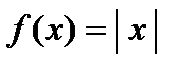непрерывна в точке 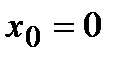. Однако в этой точке производная не существует, так как слева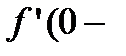 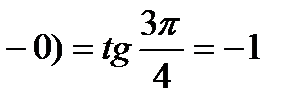, а справа 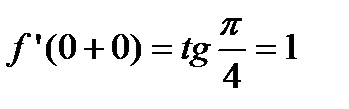. Отсюда следует, что в точке 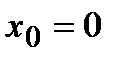производной нет.

Пример Дифференцируема ли функция 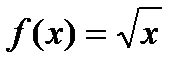в точке .

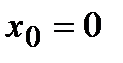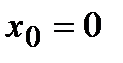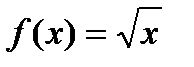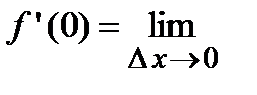
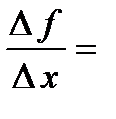
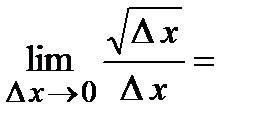
В точке данная функция непрерывна (доказать самостоятельно), однако в данной точке производная равна 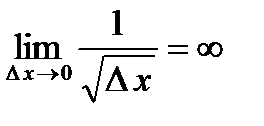, т.е. в точке 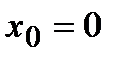производная бесконечна.

Правила дифференцирования.

1). Производная от суммы (разности) двух функций равна сумме (разности) производных от этих функций, т.е. .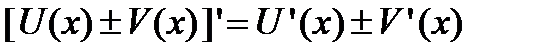

Док-во. Пусть 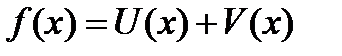, тогда в приращенной точке функция равна

.

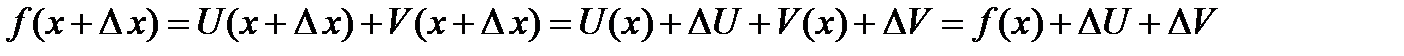Приращение функции будет равно: 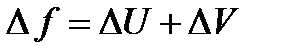, а значит производная от приведенной функции

.

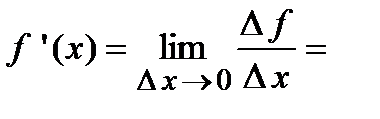
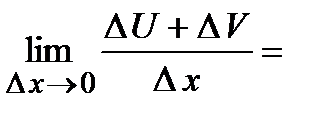
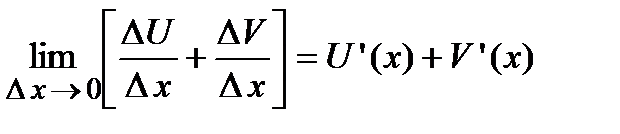Производная от суммы (разности) любого числа функций равна сумме (разности) производных от этих функций.

2). Производная от произведения двух функций вычисляется по формуле:

.

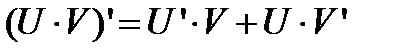Док-во. Пусть 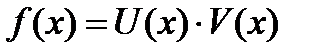, тогда в приращенной точке функция равна

.

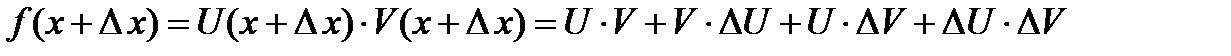Приращение функции будет равно: 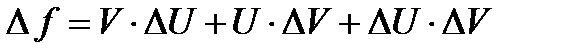, а значит производная от приведенной функции

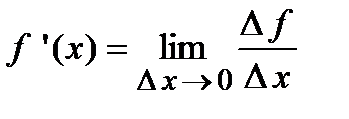
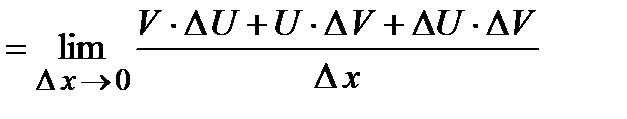
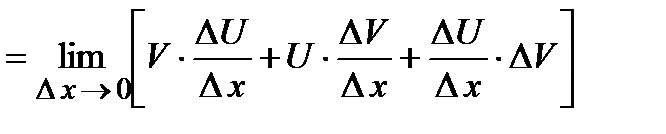(так функции непрерывны, то при и приращение )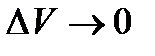

= .

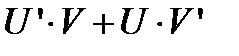3). Производная от частного двух функций вычисляется согласно формуле:

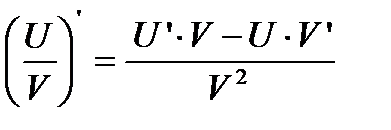(доказать самостоятельно).

4). Производная от обратной функции вычисляется по формуле: .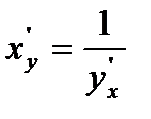

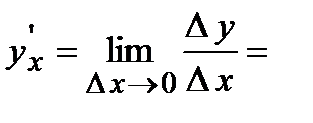
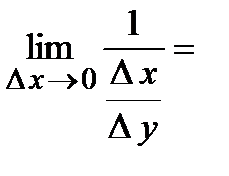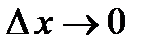Док-во. Так как (при и приращение 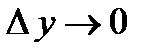, следовательно,) 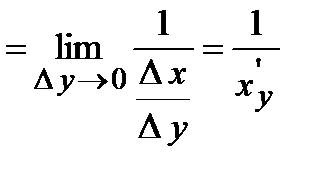или .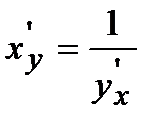

5). Производная от сложной функции 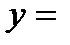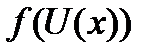вычисляется по формуле:

.

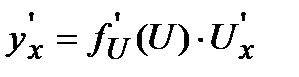Док-во. Так как 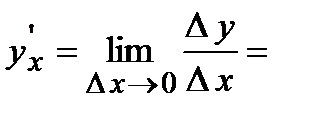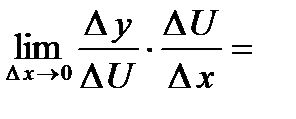(при и приращение 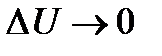, следовательно,)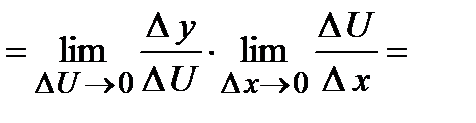 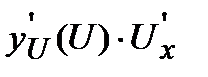или .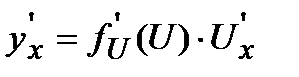

Производная от основных элементарных функций.

1). Постоянная функция 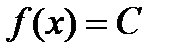. Вычислим приращение постоянной функции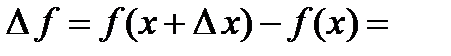 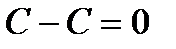. Отношение приращения функции к приращению аргумента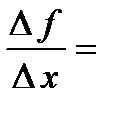 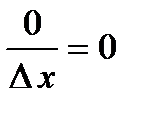. Следовательно,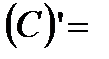 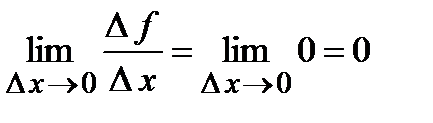, т.е. производная от постоянной величины равна нулю.

Сл1. При вычислении производной от произведения константы на функцию 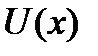получаем 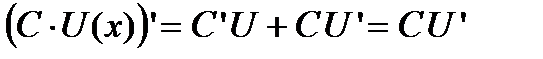, т.е. постотянный множитель можно выносить за знак производной.

Сл2. Аналогично поступают при вычислении производной от частного

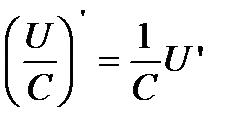или .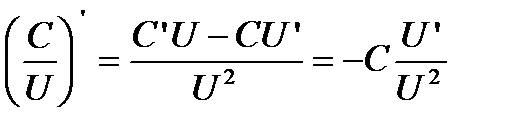

2). Логарифмическая функция 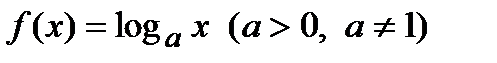. Используя определение производной, находим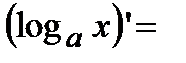

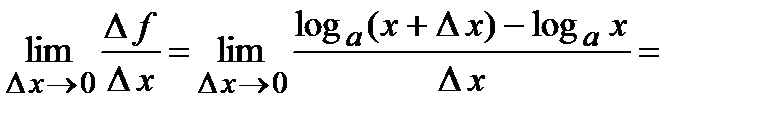
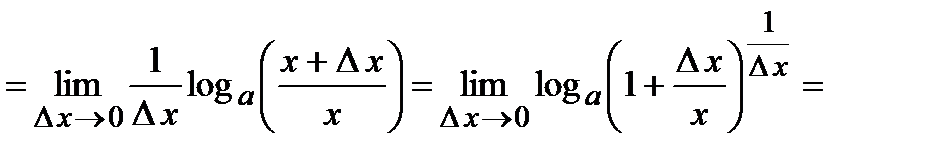
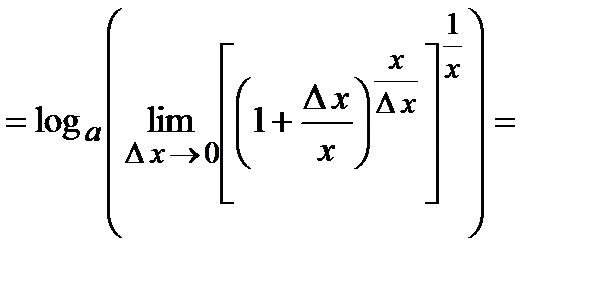(выражение в квадратных скобках стремится к числу 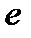по второму замечательному пределу) .

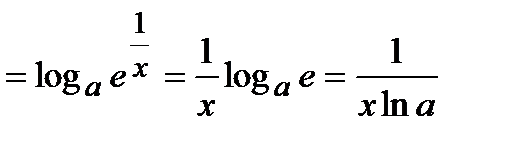Сл1. Производная от сложной логарифмической функции равна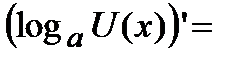

.

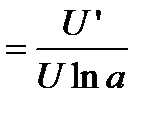Сл2. Если основание логарифма 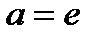, то .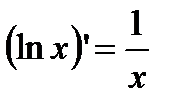

3). Степенная функция 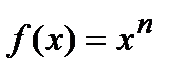. Для нахождения производной от этой функции воспользуемся методом логарифмического дифференцирования, то есть 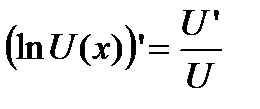. Возьмем натуральный логарифм от степенной функции 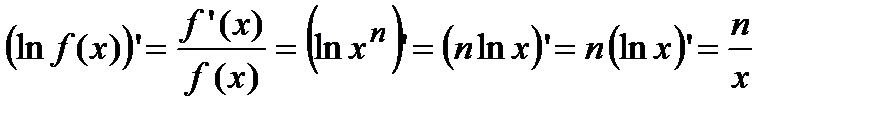. Отсюда находим 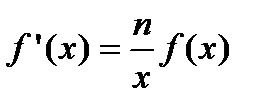. Таким образом, 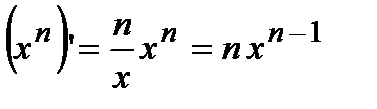. Для сложной функции эта формула имеет следующий вид .

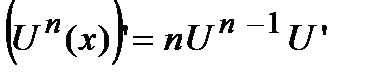Сл. Наиболее распространенными являются случаи:

а) 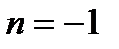: 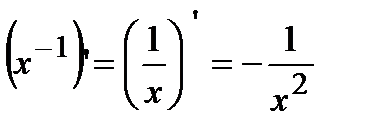(см. Сл2. для постоянной функции этого пункта);

б) 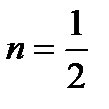: 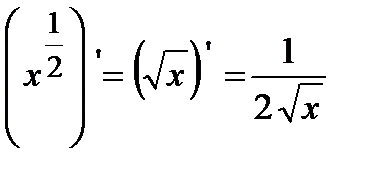; в) : .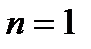

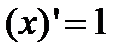4). Показательная функция 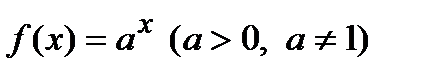. Воспользуемся логарифмическим дифференцированием 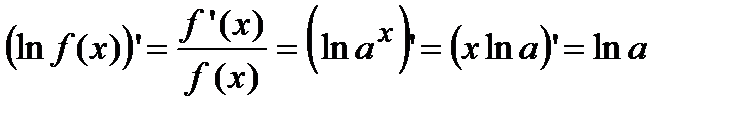. Отсюда находим 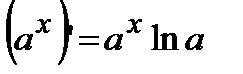. Для сложной функции эта формула имеет следующий вид .

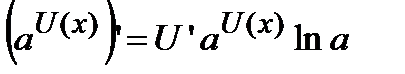Сл. Если основание показательной функции 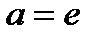, то 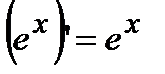. В случае сложной функции производная равна .

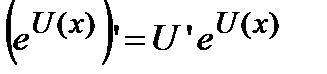5). Тригонометрические функции: а) 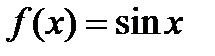. Вычислим производную от синуса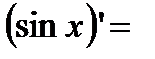

.

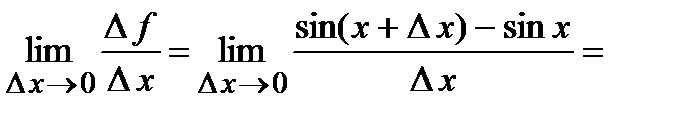
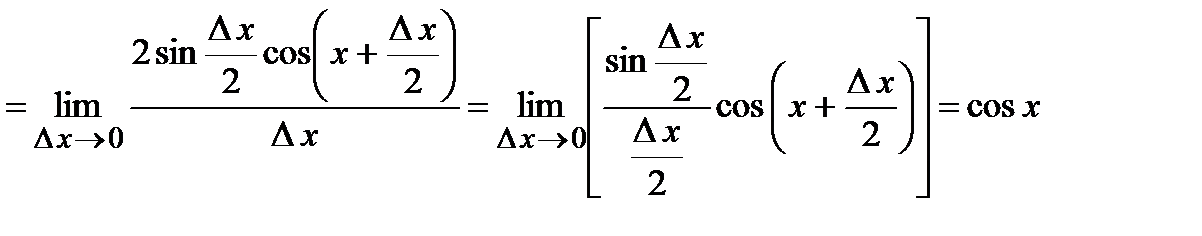При выводе формулы был использован первый замечательный предел. Для сложной функции производная равна .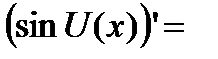

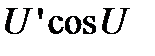Самостоятельно получить формулы для других тригонометрических функций:

б) . ; .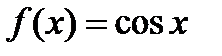

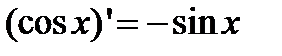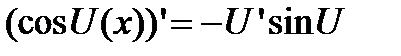в) . ; .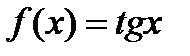

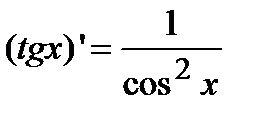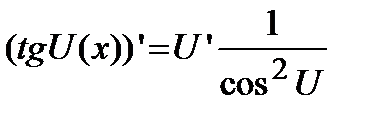г) . ; .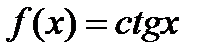

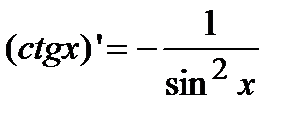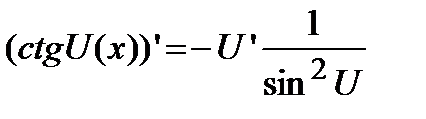6). Обратные тригонометрические функции:

а) 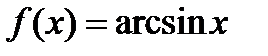. Вычислим производную от арксинуса, для чего от обеих частей равенства возьмем функцию синус, то есть найдем обратную функцию 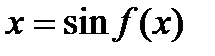. Беря производную от обеих частей равенства с учетом того факта, что функция, стоящая справа, является сложной, получим

.

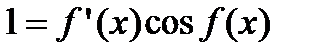Отсюда находим, что .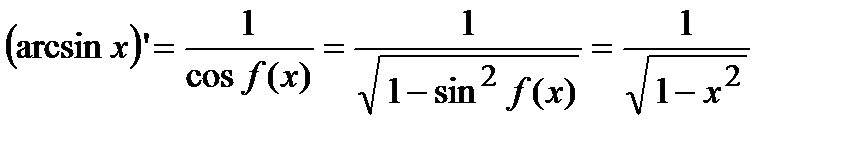

Для сложной функции 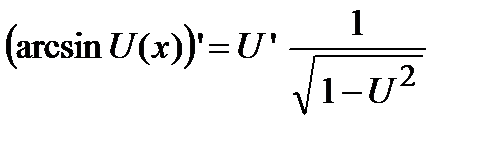. Самостоятельно получить формулы для других обратных тригонометрических функций:

б) ; ; .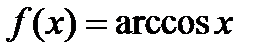

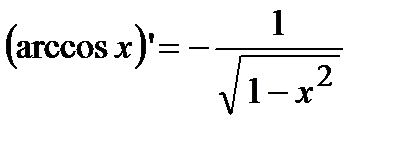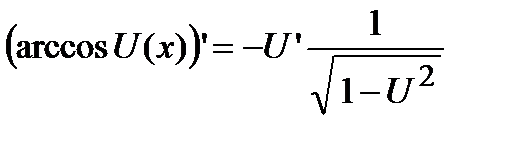в) ; ; .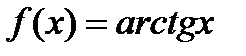

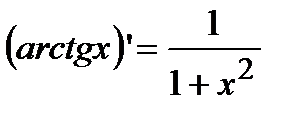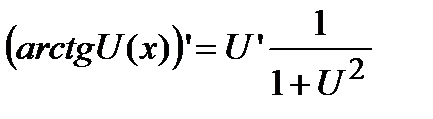г) ; ; .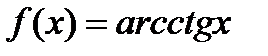

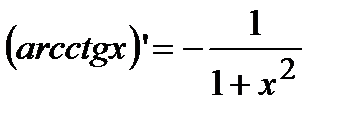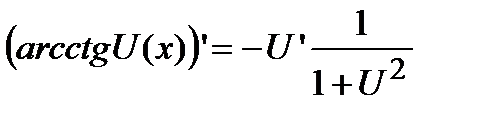Пример Найти производную функции .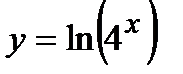

По правилу дифференцирования сложной функции и с учетом выражения для логарифмической и показательной функций имеем .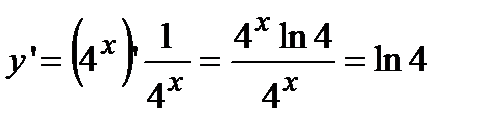

Пример Найти производную функции .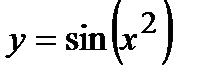

В данном случае производная .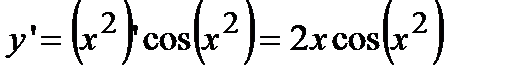

Полученные производные от элементарных функций сведем в таблицу:

№ п/п	Функция	Производная элементарной функции	Производная сложной функции

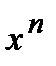
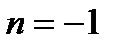
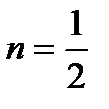
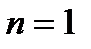
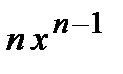
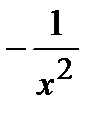
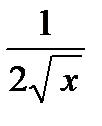
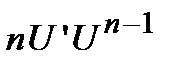
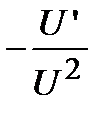
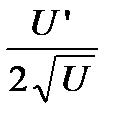
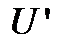
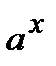
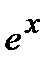
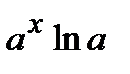
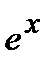
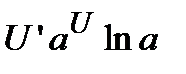
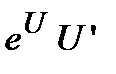
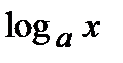
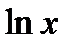
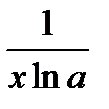
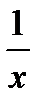
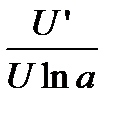
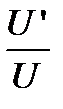
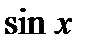
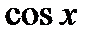
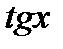
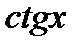
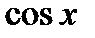
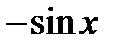
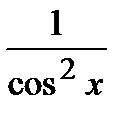
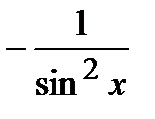
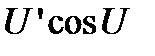
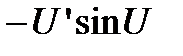
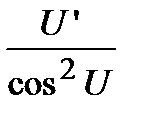
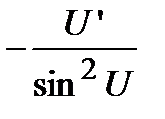
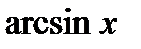
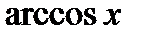
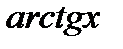
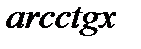
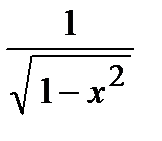
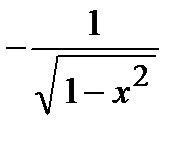
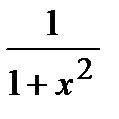
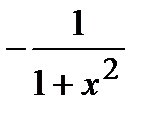
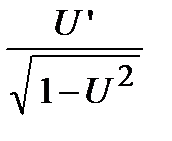
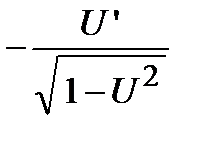
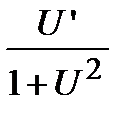
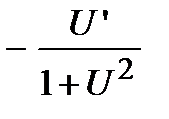
Производная от параметрически и неявно заданных функций.

Опр. Если функция 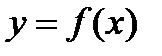задается в виде системы уравнений 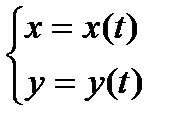, то говорят, что функция задана в параметрическом виде.

Чтобы продифференцировать параметрически заданную функцию, надо из первого уравнения системы найти обратную функцию 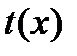и подставить ее во второе уравнение системы. В результаты этих действий получается сложная функция, производная от которой равна 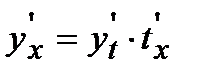. Так как производная от обратной функции связана с производной исходной функции равенством 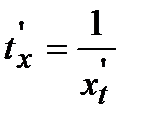, то формула для производной от параметрически заданной функции принимает вид: .

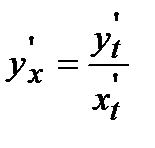Пример. Найти производную функции .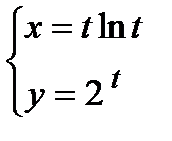

Вычислим производные от заданных функций по параметру :

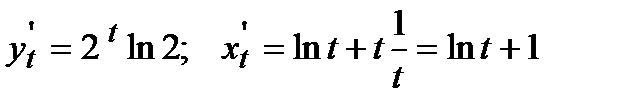. Следовательно, .

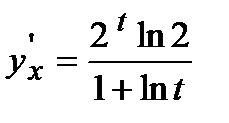Опр. Если функция 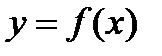задается в виде соотношения 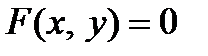, из которого нельзя явно выразить переменную 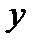через 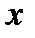или наоборот, то говорят, что функция задана в неявном виде.

Дифференцирование таких функций осуществляется с учетом того, что переменная 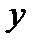является сложной функцией, т.е. зависит от переменной .

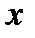Пример Найти производную функции .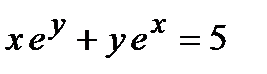

Продифференцируем данное соотношение с учетом вышеизложенного материала получим 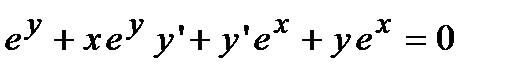. Отсюда находим, что 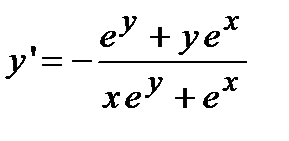. С учетом исходного равенства полученное выражение определяет производную от неявно заданной функции.

Опр. Производная от первой производной функции называется второй производной функции, т.е. .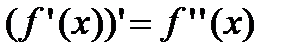

Аналогично вводятся дифференциалы и производные высших порядков:

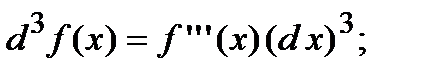
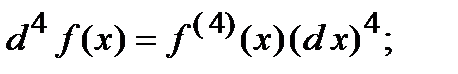и так далее.

Отметим, что обозначение производной, начиная с четвертой, берется в скобки.

Производные высших порядков могут быть записаны в виде

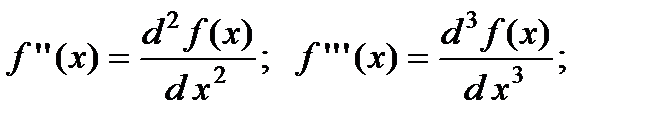и т. д.