Законы механического подобия
ОСНОВЫ ТЕОРИИ ПОДОБИЯ, МОДЕЛИРОВАНИЯ
И АНАЛИЗА РАЗМЕРНОСТЕЙ
Основные положения
Решение дифференциальных уравнений гидродинамики охватывает ограниченный круг задач. В ряде случаев аналитическое решение сопряжено со значительными математическими трудностями. В частности, не всегда можно получить удовлетворительный результат и с помощью численных методов. В таких случаях на помощь приходят экспериментальные методы исследования.
Цель этих исследований состоит в том, чтобы получить данные, необходимые для расчета других процессов, родственных изучаемому.
Эксперименты проводятся на специально создаваемых модельных установках, моделирующих определенным образом исследуемые устройства и протекающие в них физические процессы.
Известны физический и математический методы моделирования.
При физическом моделировании исследуемая модель обычно выполняется в меньшем масштабе, чем оригинал (натура), и воспроизводит изучаемое явление с сохранением его физической природы.
Математическое моделирование осуществляется путем изучения явлений, имеющих иное, чем исследуемый процесс, физическое содержание, но описываемых аналогичными математическими уравнениями.
Законы механического подобия
Полученные на модели результаты опытных исследований обобщаются и затем переносятся на натуру. Выполнение этой процедуры требует знаний законов, связывающих между собой величины, полученные при исследованиях на модели, и соответствующие им величины в натуре.
Эти законы называются законами подобия. Они устанавливают определенные соотношения между геометрическими размерами, кинематическими и динамическими характеристиками потоков в модели и натуре.
Законы подобия подробно изучаются в специальных курсах теории подобия и моделирования.
Следует отметить, что теория подобия имеет большое теоретическое и практическое значение не только для моделирования различных явлений и процессов, но и прежде всего для научного обоснования экспериментальных исследований, обработки их результатов и построения на их основе рациональных эмпирических формул.
Следует иметь в виду, что динамическое или вообще физическое подобие является обобщением геометрического подобия.
Рассмотрим способы получения масштабных коэффициентов для геометрического, кинематического и динамического подобия.
4.2.1. Геометрическое подобие
Пусть имеем натурный объект (поток) (рис.4.1), подлежащий гидродинамическому исследованию, и его модель.
Рис.4.1
Обозначим геометрические размеры объекта (натурного потока) индексом 1, а модельного – индексом 2.
Чтобы получить область течения в модели, геометрически подобную натурному потоку, разделим все линейные размеры натурного потока на некоторое число 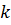 , которое называется линейным масштабом. Таким образом, получаем связь между геометрическими размерами
, которое называется линейным масштабом. Таким образом, получаем связь между геометрическими размерами 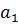 и
и 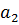 ,
, 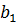 и
и 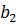 , в виде равенств:
, в виде равенств:
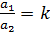 и
и 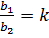 . (4.1)
. (4.1)
Линейные размеры, связанные соотношением (4.1), называют соответственными, или сходственными.
Точки, координаты которых удовлетворяют этому соотношению, называют сходственными.
Безразмерные координаты сходственных точек одинаковы.
Обычно за единицу измерения всех линейных величин в соответствующих потоках принимают 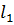 (натура),
(натура),  (модель) и находят линейный масштаб
(модель) и находят линейный масштаб  :
:
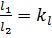 . (4.2)
. (4.2)
Для площадей и объемов соответственно имеем:
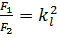 ;
; 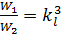 . (4.3)
. (4.3)
Очевидно, что для геометрических подобных потоков необходима пропорциональность соответствующих площадей и объемов.
7.2.2. Кинематическое подобие
Кинематическое подобие обязательно включает в себя геометрическое подобие, т.е. для кинематического подобия необходимо, чтобы траектории частиц обоих потоков были подобны геометрически.
Кроме того, для кинематически подобных потоков отрезки траекторий соответствующих частиц натурного и модельного потоков, а также отрезки времени, в течение которых протекают соответствующие процессы в натуре и в модели, должны быть пропорциональны.
Другими словами, если в первом потоке (натуре) частицы проходят путь 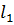 за время
за время 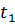 , то во втором потоке (модели) – путь
, то во втором потоке (модели) – путь  за
за 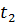 .
.
Причем, отрезки 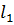 и
и  должны быть геометрически подобны, а отношение
должны быть геометрически подобны, а отношение  должно быть одинаковым для сходственных точек обоих потоков.
должно быть одинаковым для сходственных точек обоих потоков.
Отношение  называется масштабом времени и обозначается
называется масштабом времени и обозначается 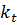 . Например, для скоростей частиц жидкости в сходственных точках потока легко получить следующие выражения:
. Например, для скоростей частиц жидкости в сходственных точках потока легко получить следующие выражения:
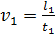 ,
, 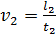 .
.
Тогда
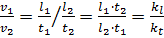 .
.
Очевидно, что
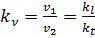 .
.
Аналогично находим масштаб ускорений:
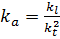 .
.
Таким образом, скорости и ускорения в сходственных точках потока связаны соотношениями
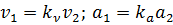 . (4.4)
. (4.4)
4.2.3. Динамическое подобие
Динамическое подобие обязательно включает в себя геометрическое и кинематическое подобия. В любых потоках, если физическая природа действующих на жидкость сил одинакова и силы образуют геометрически подобные силовые многоугольники, они являются динамически подобными.
В динамически подобных потоках отношение одноименных сил в сходственных точках в натуре и на модели постоянны, т.е.
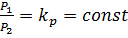 , (4.5)
, (4.5)
где 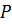 - любая сила, в том числе и равнодействующая;
- любая сила, в том числе и равнодействующая;
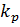 – масштабный коэффициент, или масштаб сил.
– масштабный коэффициент, или масштаб сил.
К силам, действующим в потоке жидкости, можно отнести: силы внутреннего трения жидкости, силы тяжести, силы поверхностного натяжения и др.
Для динамически подобных потоков отношение плотностей жидкости в натуре и на модели должно быть постоянным:
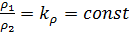 . (4.6)
. (4.6)
Обозначим действующие в сходственных точках натурного и модельного потоков силы 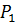 и
и  соответственно. По основному уравнению динамики, известному из теоретической механики, сила равна произведению массы на ускорение:
соответственно. По основному уравнению динамики, известному из теоретической механики, сила равна произведению массы на ускорение:
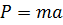 ,
,
где 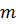 – масса жидкости;
– масса жидкости;
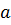 – ускорение.
– ускорение.
Учитывая, что масса равна произведению плотности на ее объем
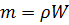 ,
,
где 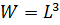 ,
,
тогда
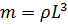 .
.
Ускорение определяется приращением скорости 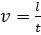 в единицу времени
в единицу времени 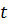 , т.е.
, т.е. 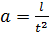 .
.
Следовательно,
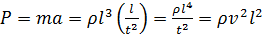 . (4.7)
. (4.7)
Таким образом, для динамического подобия необходимо, чтобы силы находились в соотношении
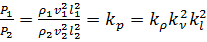 . (4.8)
. (4.8)
Выражение (4.8) является математическим выражением общего закона динамического подобия, впервые сформулированным Ньютоном.
Преобразуем выражение (4.8) к виду
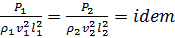 . (4.9)
. (4.9)
Следовательно, 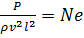 – критерий Ньютона. Критерий Ньютона является обобщенным критерием динамического подобия механических систем.
– критерий Ньютона. Критерий Ньютона является обобщенным критерием динамического подобия механических систем.
В гидродинамических исследованиях во многих случаях оказывается невозможным найти количественные оценки действующих внешних сил, а следовательно, и их равнодействующей. Поэтому при исследованиях гидравлических явлений часто выделяют только одну силу, а действием остальных пренебрегают. В этом случае применяют частные критерии Рейнольдса, Фруда, Вебера и др.
Дата добавления: 2016-06-05; просмотров: 4319;











