Физическое моделирование

Физическое моделирование находит широкое применение при опытных исследованиях в области гидравлики. Моделирование основано на создании модели, имеющей ту же физическую природу, что и процессы, протекающие в натуре. Достоинством этого метода является возможность изготовления модели в любом произвольном масштабе и применения на модели любой жидкости.

Обычно модель выполняется меньших размеров, чем в натуре, что значительно удешевляет и упрощает проведение опытов. Полученные результаты опытов обрабатываются и обобщаются с целью переносов их на натуру. Физическое моделирование базируется на законах теории механического подобия и теории размерностей.

На практике обычно применяется частичное, или приближенное, моделирование. В этом случае модель исследуется по основным признакам, соответствующим реальному процессу.

При частичном моделировании используются свойства приближенного подобия по одному из определяющих критериев.

В этом случае основной задачей является определение связи между определяющими и неопределяющими критериями, а также нахождение масштабов для основных физических величин.

Непременным условием при физическом моделировании является строгое геометрическое подобие модели и натуры, а также равенство в них соответствующих критериев подобия.

Рассмотрим примеры частичного физического моделирования.

Пример 1. Частичное моделирование по критерию Рейнольдса.

Если при движении жидкости преобладающими силами, определяющими движение жидкости или газа, являются сила трения и инерции, то моделирование проводится по критерию .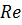

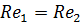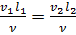или . (4.22)

Причем вязкость жидкости на модели и в натуре одна и та же, то есть .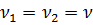

Соотношение (4.22) принимает вид:

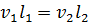или 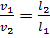. (4.23)

Отсюда просто определяется масштаб скоростей:

.

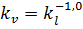Масштабы других физических величин находятся следующим образом.

Например, определение масштаба расхода вычисляется из уравнения расхода

.

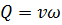Для динамических подобных потоков определяется комбинация масштабных коэффициентов, с учетом соотношения (4.23):

,

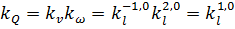где 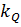– масштаб расхода;

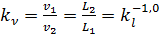– масштаб скорости;

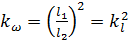– масштаб площади

По аналогии можно получить масштабы других физических величин.

При частичном моделировании по критерию Рейнольдса, одним из основных признаков динамического подобия потоков с преобладающим действием сил трения является равенство коэффициентов гидравлического сопротивления по длине, то есть .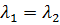

Это свойство широко используется при моделировании по критерию Рейнольдса.

Пример 2. Частичное моделирование по критерию Фруда.

Моделирование по критерию Фруда применяется при изучении потоков, в которых преобладают силы инерции и тяжести, например при изучении гидравлических струй и др.

Динамическое подобие потоков обеспечивается равенством критерия Фруда на натуре и модели.

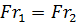или, при условии, что :

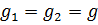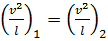. (4.24)

Из соотношения (4.24) определим масштаб скоростей:

.

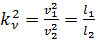Отсюда 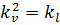или .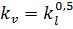

Аналогично можно получить масштабы других физических величин.

Пример 3. Предположим, что исследуется движение вязкой жидкости в трубопроводе, в котором при моделировании следует учитывать как силы внутреннего трения жидкости, обусловленные ее вязкостью, так и массовые гравитационные – силы тяжести.

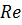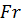Для обеспечения полного динамического подобия требуется равенство критериев и на модели и в натуре.

Для одних и тех же гравитационных условий принимаем .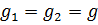

Тогда при моделировании по Рейнольдсу отношение средних скоростей движения жидкости в трубопроводе (натурном и модельном) должно удовлетворять условию:

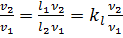. (4.25)

При моделировании по Фруду

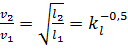. (4.26)

Сопоставляем полученные выражения (4.25) и (4.26) и находим

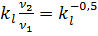или .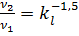

Отсюда

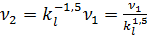. (4.27)

Из выражения (4.27) следует, что для соблюдения полного динамического подобия в модели должна применяться жидкость кинематическая вязкость которой 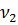будет в 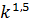раз меньше 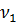натурной жидкости.

Например, если при моделировании принять линейный масштаб 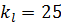,то

.

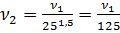Очевидно, что найти жидкость со столь малой вязкостью практически невозможно.

Это указывает на то, что при реальных масштабах физических величин подтверждается несовместимость двух основных критериев подобия: 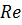и .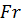

Кроме того, очевидна невозможность полного динамического подобия потоков одной и той же жидкости.

4.5. Анализ размерностей. 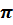– теорема

При организации экспериментов необходимо с самого начала установить наиболее целесообразную методику их проведения и порядок обработки результатов опытов.

В практике гидравлических исследований метод анализа размерностей нашел широкое применение. Этот метод позволяет заранее определить основные критерии подобия, в которых следует обрабатывать результаты опытов, а также обобщать их и устанавливать закономерности, отражающие исследуемый процесс.

Исходным для метода анализа размерностей является то, что любое математическое уравнение, описывающее физический процесс, обязательно должно быть размерно однородным.

Это означает, что обе его части имеют всегда одинаковую размерность независимо от выбора системы физических величин.

Свойство однородности является основой теории размерностей. В механике в качестве основных физических величин принимают длину 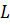, массу 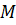и время 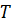. Они независимы друг от друга.

В механике жидкости и газа не всегда удается воспользоваться основными физическими величинами, тогда принимаются любые, независимые друг от друга, например, плотность, скорость, время.

Достоинством метода является то, что при его применении достаточно знать основные переменные величины, характеризующие данный процесс, само же уравнение, описывающее этот процесс, может быть неизвестно.

Обычно задача анализа размерностей решается путем определения физических величин, которые полностью характеризуют данный процесс. Затем устанавливается характер зависимости между выделенными величинами, исходя из принципа однородности размерности с помощью так называемой 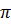-теоремы.

Сущность 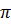–теоремы состоит в следующем. В общем случае 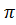–теорема устанавливает связь между теорией подобия и теорией размерностей.

Предположим, что переменная величина 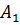зависит от ряда переменных: 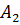, ,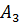…, , 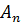участвующих в каком-либо физическом процессе, и не зависит от каких-либо других переменных.

Тогда общая функциональная зависимость между этими величинами может быть представлена уравнением

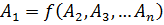(4.28)

или

.

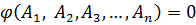Пусть число определяющих размерных единиц, через которое могут быть выражены все 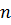– переменные, равно .

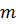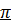–теорема формулируется так:

Уравнение, связывающее между собой 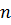размерных физических величин, характеризующих рассматриваемое явление, среди которых 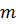обладают независимой размерностью, может быть преобразовано в 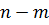безразмерных комплексов, составленных из указанных величин.

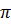–теорема устанавливает, что если указанные 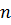переменных выразить через эти основные единицы, то их можно сгруппировать в 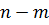безразмерных 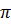-членов:

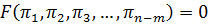, (4.29)

где каждый комплекс 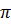представляет собой безразмерное произведение нескольких 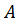, то есть число членов в физическом уравнении сокращается до 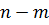. Причем каждый такой 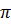-член будет содержать 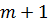переменную величину. В гидродинамических задачах число таких переменных, входящих в 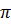-члены, должно равняться четырем.

Три из них – определяющие: характерный размер (диаметр 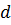), скорость течения жидкости 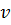и ее плотность 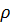(или вязкость 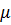) входят в каждый из 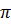-членов и только четвертая переменная заменяется другой при переходе от члена к члену.

Для удобства исследования показатели последних принимаются равными -1. Показатели степени определяющих переменных неизвестны. Обозначим их 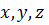с индексами, соответствующими индексам 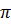-членов.

Таким образом, имеем:

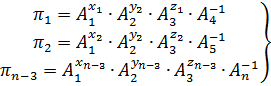. (4.30)

Выражаем затем входящие в -члены переменные через основные независимые размерности, но, поскольку эти члены являются безразмерными во всех полученных для них выражениях, то показатели степени каждой из основных размерностей должны обязательно равняться нулю.

Пример. Движение сферы в жидкости.

Рассмотрим задачу о поступательном движении сферы с постоянной скоростью внутри безграничной массы жидкости, заполняющей все пространство вне сферы.

Пусть диаметр сферы d, скорость ее движения v. Жидкость будем считать несжимаемой. Свойства инерции и вязкости жидкости будем принимать во внимание. Распределение давлений на поверхности тела и суммарные силы, действующие со стороны жидкости на тело, зависят от состояния возмущенного движения жидкости.

Для сферы установившееся состояние движения жидкости определяется системой четырех параметров:

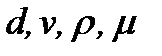
Обозначим через 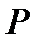силу, действующую со стороны жидкости на сферу.

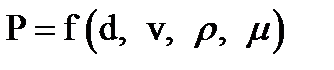
или

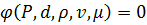.(4.32)

В задачах прикладной механики жидкости и газа имеются три физические величины, имеющие независимые размерности: масса 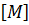, время 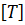, длина 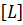, то есть в этих задачах следует принимать 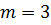. Это позволяет составить уравнение размерностей для каждого 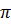-члена, соблюдая при этом обязательное условие их размерной однородности. Так как число основных размерных величин равно трем 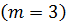, а переменных величин в уравнении (4.32) пять 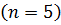, то получим уравнение, состоящее из 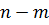безразмерных 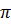-членов:

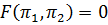.(4.33)

Каждый 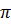-член должен содержать четыре переменные величины. Принимаем в качестве определяющих переменных величин следующие:

- диаметр сферы ;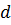

- скорость движения сферы ;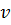

- плотность жидкости .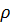

Комбинируя их поочередно с остальными переменными, входящими в уравнение (4.32), получим:

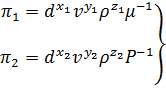. (4.34)

Запишем размерности переменных величин, входящих в 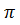-члены системы (4.34):

; ; ;

; ;

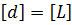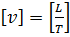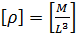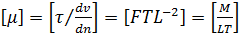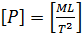Составим уравнения размерностей для каждого из 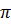-членов, имея в виду обязательное условие их размерной однородности. Для первого члена имеем

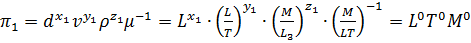. (4.35)

Найдем степени размерностей в левой части уравнения (4.35):

.

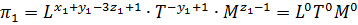Приравнивая к нулю показатели степени при одинаковых основаниях 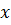, получим систему уравнений с неизвестными :

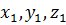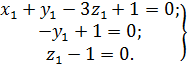(4.36)

Из совместного решения уравнений (4.36) находим:

.

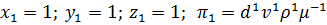Подставив эти значения показателей степени в первый 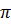-член системы уравнений (4.34), получим

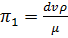, (4.37)

где найденное значение 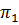представляет собой критерий Рейнольдса: .

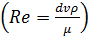Для второго 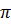-члена имеем

.

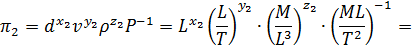
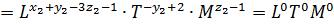Отсюда запишем систему уравнений:

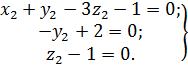
Находим :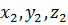

.

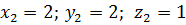Запишем выражение для второго 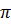-члена с учетом показателей степени:

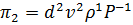
или

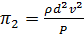. (4.38)

Подставив значения 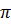-членов в соотношение (4.33), получаем уравнение:

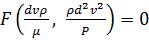. (4.41)

Решая уравнение (4.41) относительно 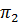, находим

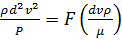. (4.42)

или

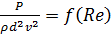(4.43)

Таким образом, получили, что безразмерная величина 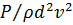является функций числа Рейнольдса.

Предельный случай малой вязкости

Полагая 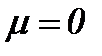, получаем, что n=4 ( 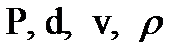), а n-m=1, т.е. остается один безразмерный комплекс

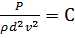, или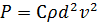

Сила сопротивления пропорциональна квадрату скорости и не зависит от числа Рейнольдса.

Предельный случай малых чисел Рейнольдса

При уменьшении числа Рейнольдса роль сил вязкости увеличивается. Если мы пренебрежем силами инерции по сравнению с силами вязкости, то это равносильно допущению о несущественности параметра 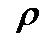. В этом случае можно получить, что

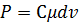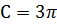( , Стокс, 1851)

Сила сопротивления пропорциональна скорости, вязкости и диаметру сферы. Этот закон, который называется законом Стокса, хорошо согласуется с опытами при малой скорости движения малых тел, например, при оседании мелких частиц в жидкости.

Таким образом, анализ размерности позволил выяснить вид функции 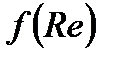в зависимости от числа Рейнольдса при весьма малых и весьма больших значениях числа Рейнольдса. При 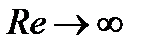мы приходим к идеальной (невязкой) жидкости; в этом случае 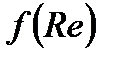стремится к некоторой константе, независящей от числа Рейнольдса. Режимы движения, соответствующие малым значениям числа Рейнольдса, характеризуются тем, что вязкость жидкости имеет основное значение, а свойство инерции – второстепенное – большие значения для 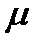, малые – для 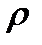. В пределе при 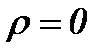справедлива формула Стокса; принимая 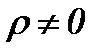из этой формулы получим

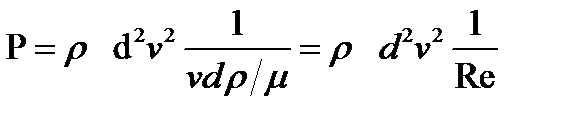
Рис.4.2 Коэффициент сопротивления шара 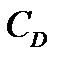в функции числа Рейнольдса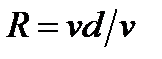

Результаты опытов по определению силы сопротивления частиц обычно представляют в виде зависимости коэффициента сопротивления 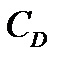от числа Рейнольдса 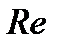. Величина 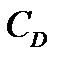находится по определению как отношение силы сопротивления 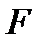к произведению динамического напора 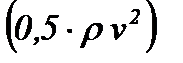на площадь миделевого сечения частицы (в случае шара 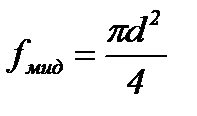). Введение коэффициента сопротивления 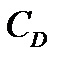позволяет представить формулу Стокса в виде

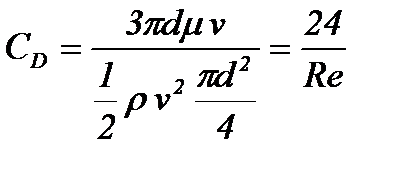
Сравнение этой формулы с результатами опытных измерений показывает, что высокая точность расчетов по ней имеет место лишь при 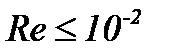. Однако практически вплоть до 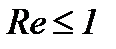использование формулы Стокса допустимо (погрешность в расчете при этом не превосходит 10%).