МЕТОДИКА 22. Прямоугольная система координат на плоскости, абсцисса и ордината точки


Виленкин 6 кл. Тема изучается в 6 классе в большой теме «Координаты на плоскости». Основные понятия: координатные прямые, система координат, абсцисса, ордината.

Типы математических ошибок по данной теме: не различают понятия, такие как абсцисса и ордината, положительные и отрицательные числа, направление положительной оси координат, ошибки при построении точки на плоскости координат.

Учебные задачи на устроение ошибок:

  • Постройте точку по ее координатам
  • Определите координаты заданной на плоскости точки
  • Задания вида «рисуем по координатам»
  • Как определить положение точки на прямой, на плоскости
  • Как располагаются координатные прямые
  • Где лежит точка, если ее абсцисса равно нулю, ордината равна нулю.

Методы и средства проверки знаний и умений учащихся.

Контроль знаний и его типы:

  • Внешний (учитель за учеником)
  • Взаимный (ученик за учеником)
  • Самоконтроль (ученик за собственной деятельностью)

Виды контроля:

  • Контроль по конечному результату: пошаговый (контроль за операциями), контроль за установлением определенных параметров деятельности
  • По месту в процессе обучения: текущий (в ходе учения), итоговый по теме, по курсу обучения. Текущий может быть: предварительный (установить готовность к обучению), ежедневный, периодический.
  • В новых педагогических технологиях рассматриваются следующие виды контроля усвоения знаний и способов деятельности: входной, текущий, итоговый.

Формы контроля:

  • Массовый
  • Индивидуальный: фронтальный, индивидуальный опрос, контрольные работы, сочинения, диктанты.

Способы контроля: письменный, устный, практический.

Средства контроля: математический диктант, дидактические материалы, карточки, тесты, перфокарты, таблицы, опорные схемы, задания с печатной основой, компьютер, модели и приборы и т.д.

К современным средствам относятся: тест, рейтинговые системы, портфолио (учитывать творческие работы, подходы учащихся).

Фрагмент урока на этапе контроля.

Деятельность учителя Деятельность учащихся
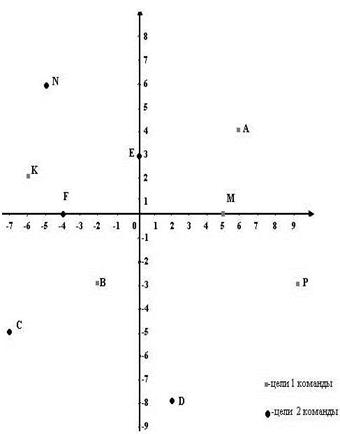
Ребята, давайте теперь посмотрим как вы усвоили материал. Как построить точку С на координатной плоскости, если ее координаты (–4; 3).   Игра “Поражение цели”. Класс делится на две команды: “Наводчики” и “Стрелки”. По очереди каждая команда поражает цель своего противника. Чья команда поразит больше цели!       Необходимо отложить на координатных осях абсциссу и ординату точки С. Абсцисса равна -4, т.е. откладываем от начала координат влево 4 единицы. Ордината равна 3, т.е. откладываем от начала координат три единицы вверх. Мысленно проводим прямые, параллельные осям координат, в данных точках; и точка пересечения этих прямых и является искомой точкой С.  

 

Типы математических ошибок по данной теме: не различают понятия, такие как абсцисса и ордината, положительные и отрицательные числа, направление положительной оси координат, ошибки при построении точки на плоскости координат.

Учебные задачи на устроение ошибок:

  • Постройте точку по ее координатам
  • Определите координаты заданной на плоскости точки
  • Задания вида «рисуем по координатам»
  • Как определить положение точки на прямой, на плоскости
  • Как располагаются координатные прямые
  • Где лежит точка, если ее абсцисса равно нулю, ордината равна нулю.

Методы и средства проверки знаний и умений учащихся.

Контроль знаний и его типы:

  • Внешний (учитель за учеником)
  • Взаимный (ученик за учеником)
  • Самоконтроль (ученик за собственной деятельностью)

Виды контроля:

  • Контроль по конечному результату: пошаговый (контроль за операциями), контроль за установлением определенных параметров деятельности
  • По месту в процессе обучения: текущий (в ходе учения), итоговый по теме, по курсу обучения. Текущий может быть: предварительный (установить готовность к обучению), ежедневный, периодический.
  • В новых педагогических технологиях рассматриваются следующие виды контроля усвоения знаний и способов деятельности: входной, текущий, итоговый.

Формы контроля:

  • Массовый
  • Индивидуальный: фронтальный, индивидуальный опрос, контрольные работы, сочинения, диктанты.

Способы контроля: письменный, устный, практический.

Средства контроля: математический диктант, дидактические материалы, карточки, тесты, перфокарты, таблицы, опорные схемы, задания с печатной основой, компьютер, модели и приборы и т.д.

К современным средствам относятся: тест, рейтинговые системы, портфолио (учитывать творческие работы, подходы учащихся).

Билет № 23.Плоскость в пространстве.

Пусть в пространстве E3 задана некоторая аффинная система координат и плоскость p.

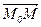I. Каноническое уравнение плоскости.Выберем произвольную точку M0(x0 ; y0 ; z0 ) Î p и от неё отложим любые неколлинеарные векторы a = и b = 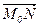с концами M, N Î p. Тогда плоскость p однозначно определяется тремя точками M0 , M, N , не лежащими на одной прямой. Если а(a; b; g), b(l ; m ; n), то для любой точки X(x ; y ; z) Î E3имеем X Î p Û Û ( 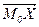, a , b компланарны) Û 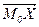×a×b = 0 Û Û 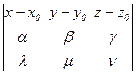= 0 . Это уравнение относительно переменных x, y, z называется каноническим уравнением плоскости p (по аналогии с каноническим уравнением прямой). Векторы a, b называются направляющими векторами плоскости. Поэтому каноническое уравнение плоскости – это уравнение, составленное по координатам одной точки плоскости (M0 Î p) и двух её направляющих векторов (а(a; b; g), b(l ; m ; n)).

Ясно, что каноническое уравнение плоскости определено неоднозначно: можно произвольно выбирать точку плоскости и направляющие векторы.

II. Параметрическое уравнение плоскости.Из теории определителей известно, что 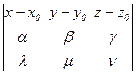= 0 Û $ s, t Î R 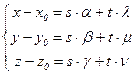Û $ s, t Î R(здесь важно, что векторы a(a ; b ; g) и b(l ; m ; n) линейно независимы). Таким образом, получаем параметрическое уравнение плоскости:

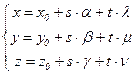,s, t Î R

Ясно, что по заданному параметрическому уравнению плоскости без труда выписывается её каноническое уравнение.

III. Общее уравнение плоскости. любая плоскость p может быть задана уравнением A×x+B×y+C×z+D = 0 (A2+B2+С2¹ 0), которое называется общим уравнением плоскости. Обратно, каждое общее уравнение A×x+B×y+C×z+D = 0 (A2+B2+С2 ¹ 0) задаёт в пространстве некоторую плоскость, направляющие векторы а(a ; b ; g) и b(l ; m ; n) которой являются произвольными линейно независимыми решениями однородного уравнения A×x+B×y+C×z = 0.

Теорема (об общем уравнении плоскости). (1) Каждая плоскость в пространстве E3 задаётся некоторым общим уравнением вида A×x+B×y+C×z+D = 0 (A2+B2+C2 ¹ 0).

(2) Каждое общее уравнение A×x+B×y+C×z+D = 0 (A2+B2+C2 ¹ 0) однозначно определяет некоторую плоскость в пространстве E3 .

(3) Два общих уравнения плоскости A1×x+B1×y+C1×z+D1 = 0, A2×x+B2×y+C2×z+D2 = 0 (A12+B12+C12 ¹ 0 ¹ A22+B22+C22), задают одну и ту же плоскость тогда и только тогда, когда коэффициенты этих уравнений пропорциональны: 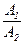= = 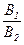= = 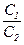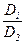l Î R \ {0}.

(4) При аффинной замене координат общее уравнение плоскости преобразуется снова в общее уравнение плоскости, т.е. вид общего уравнения плоскости инвариантен при аффинных преобразованиях координат.

IV. Уравнение плоскости в отрезках. Пусть плоскость p, не проходящая через начало аффинной системы координат и не параллельная ни одной из координатных осей Ox, Oy, Oz,задана общим уравнением A×x+B×y+C×z+D = 0 (A2+B2+C2 ¹ 0). Это значит, что A×0+B×0+C×0+D ¹ 0, т.е. D ¹ 0, и плоскость p пересекает все три координатные оси. Каковы эти точки пересечения ? 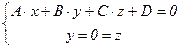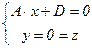Координаты точки пересечения с осью Ox удовлетворяют условию Û Û 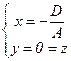. В частности, A ¹ 0. Аналогично находятся и точки пересечения плоскости p с осями Oy и Oz : (0 ; – 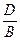; 0), (0 ; 0 ; – 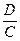) Итак, уравнение плоскости A×x+B×y+C×z+D = 0 удовлетворяет ограничениям A ¹ 0, B ¹ 0, C ¹ 0, D ¹ 0. Тогда A×x + B×y + C×z+D = 0 Û A×x + B×y + C×z = – D Û 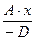+ + 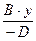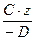= 1 Û Û 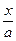+ + 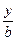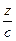= 1, где a = – 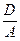, b = – 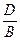, c = – 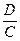– найденные выше координаты пересечения плоскости с соответствующими координатными осями.

Полученное уравнение 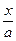+ + 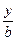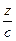= 1 называется уравнением плоскости в отрезках. Здесь величины a, b и с определяют отрезки, отсекаемые плоскостью на координатных осях (см. рис).

V. Нормальное уравнение плоскости. Плоскость можно задать уравнением A×x+B×y+C×z+D = 0, где A2+B2+C2 = 1, которое называют нормальным уравнением прямой. Смысл этого названия можно понять, если ввести следующее определение: вектор единичной длины, перепендикулярный к заданной плоскости, называется вектором нормали для этой плоскости.

Рассмотрим вектор n(A; B; C) и исследуем его расположение по отношению к плоскости. Если рассмотреть произвольный вектор 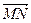, где M(x1 ; y1 ; z1 ), N(x2 ; y2 ; z2 ) Î p, то 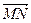(x2 – x1 ; y2 – y1 ; z2 – z1 ) и из условий A×x1+B×y1+C×z1+D = 0, A×x2+B×y2+C×z2+D = 0 следует, что n× 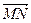= A×(x2 – x1)+B×(y2 – y1)+C×(z2 – z1) = 0. Таким образом, n ^ 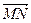и ввиду произвольности точек M, N Î p, получаем n ^ p .Если плоскость задана нормальным уравнением, то A2+B2+C2 = 1, |n| = 1, так что n(A; B; C) – вектор нормали для плоскости, заданной нормальным уравнением A×x+B×y+C×z+D = 0.

Дата добавления: 2021-12-14; просмотров: 311;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.011 сек.